1  ^?? Измерьте радиус шарика;

Методом прокатывания определяем диаметр шарика $D = 2,47 {~} см$. Радиус шарика равен $R= \frac{D}{2} = 1,24 {~}см$.

2  ^?? исследуйте зависимость $s(H)$;

Скатывая шарик с разных высот, снимаем зависимость $s(H)$. С каждой высоты шарик скатываем несколько раз, в таблице приведено среднее значение $s$.

$N$	$H, см$	$s, см$
1	0,4	4,8
2	1,1	13,0
3	1,8	21,8
4	2,5	28,8
5	3,2	35,3
6	3,9	41,0
7	5,6	58,0

3  ^?? постройте график зависимости $s(H)$;

4  ^?? определите значение коэффициента $k$.

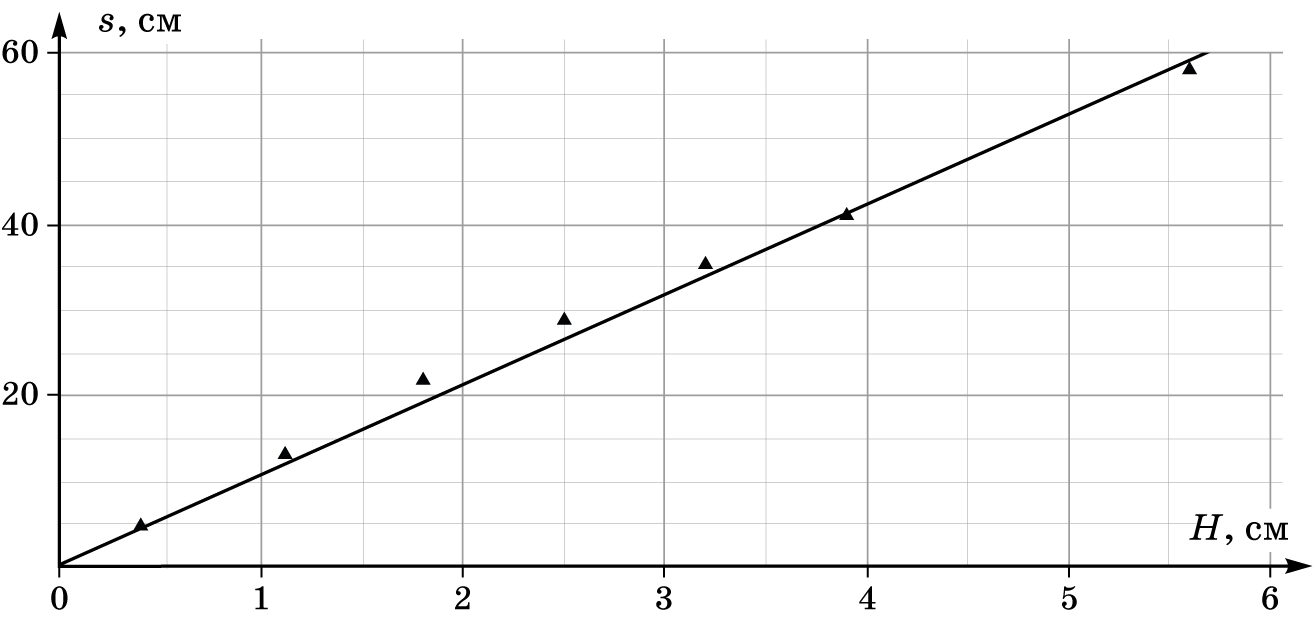
По графику определим угловой коэффициент наклона $$\frac{\Delta s}{\Delta H} = \frac{59}{5,6} \approx 10,5$$
Так как угловой коэффициент наклона равен $\frac{\Delta s}{\Delta H} = \frac{R}{k}$, то коэффициент $k$ равен $$k = \frac{R}{\frac{\Delta s}{\Delta H}} = \frac{1,24}{10,5} \approx 0,12 {~} см$$