
Силы, действующие на шарик: сила трения $\vec{F}$, сила тяготения, нормальная сила и сила Лоренца $\vec{F}_L$. Ни одна из этих сил не совершает механической работы по отношению к шарику, так что кинетическая энергия шарика не изменяется. Из условия чистого качения скорость центра шарика $v$пропорциональна угловой скорости $\omega$ движения качения, то есть полная кинетическая энергия может быть выражена через $v^2$. В результате, скорость центра шарика остается постоянной, но направление скорости может изменяться.
Полная сила Лоренца, действующая на шарик, может быть выражена через скорость центра шарика
\begin{equation}
{\vec{F}}_L=Q\,\vec{v}\times\vec{B}\ \
\end{equation}
Это можно показать, суммируя силы Лоренца, действующие на элементы шарика.
$\textbf{Доказательство 1.}$ Обозначим небольшую частицу заряда шарика за $\Delta Q_{i}$, вектор его положения, направленный от центра шарика за $\vec{x}_i$. Скорость этой частицы
$$\vec{v}_i=\vec{v}+\vec{\omega} \times \vec{x}_i$$
так что суммарная сила Лоренца может быть записана как
$$\vec{F}_L=\sum_i{\Delta Q_i\,\vec{v}_i\times\vec{B}}=\sum_i{\Delta Q_i\,\vec{v}\times\vec{B}}+\sum_i{\Delta Q_i\,(\vec\omega\times\vec x_i)\times\vec{B}}$$
Вторая сумма равна нулю, так как члены, содержащие $\vec x_i$ и $-\vec x_i$ сокращаются. В первой сумме $\vec{v}\times\vec{B}$ можно вынести за скобки, поэтому заряд $Q$ можно считать точечным и поместить его в центре масс.
Скорость центра шарика не изменяется, поэтому результирующая сила (которая горизонтальна) должна быть перпендикулярной скорости $\vec{v}$ его центра. Так как сила Лоренца всегда перпендикулярна $\vec{v}$, сила трения $\vec{F}$ тоже должна быть перпендикулярной $\vec{v}$. Величина $\vec{F}$ не может зависеть от положения шарика, а зависит только от его скорости, поэтому $\left|\vec{F}\right|$ в процессе движения не изменяется. Поэтому результирующая сила (а следовательно, ускорение центра шарика) постоянная по величине. Следовательно, шарик совершает круговое движение со скоростью $\left|\vec{v}\right|=\ v_0$ (см. рисунок).
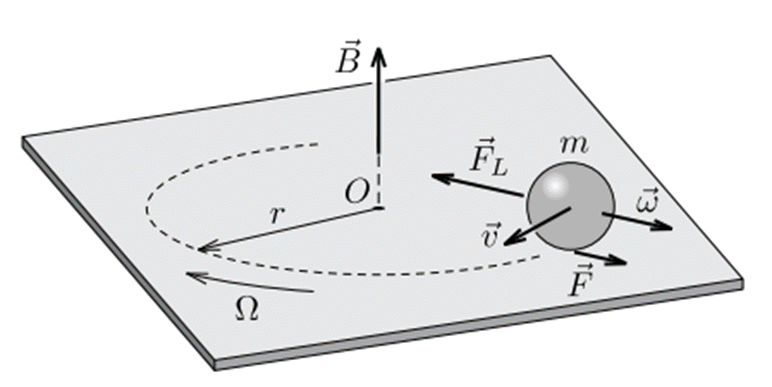
Теперь можно записать уравнение движения шарика. Ускорение центра масс направлено горизонтально и вызвано действием силы трения и суммарной силой Лоренца. С помощью уравнения второй закон Ньютона в радиальном направлении может быть записан как
$$Qvb-F=mr\Omega^2,$$
Здесь $r$ — радиус круговой траектории центра масс и $\Omega$ — угловая скорость кругового движения. Можно получить соотношение между двумя угловыми скоростями из условия чистого качения:
$$v_0=R\omega=r\Omega$$
Магнитное поле также создает крутящий момент, действующий на шарик. Момент равен
$$\vec\tau_L=\cfrac{Q}{2m}\vec L\times\vec B,$$
Здесь $\vec{L}$ — момент импульса шарика относительно его центра.
$\textbf{Доказательство 2.}$ При качении шарика по поверхности движущиеся заряды образуют замкнутые токи, которые создают магнитный момент. Небольшая частица заряда $\Delta Q_i$ соответствует току
$$I_i=\cfrac{|\vec\omega|}{2\pi}\Delta Q_i,$$
так что вклад этого элемента в суммарный магнитный момент$\vec\mu$ имеет величину $I_i\pi x^2_{i,\perp}$. Здесь $x_{i,\perp}$ — расстояние от оси вращения шарика. Направление суммарного магнитного момента параллельно вектору $\vec\omega$, а его величина может быть записана как сумма
$$\vec\mu=\cfrac{1}{2}\vec\omega\sum_i \Delta Q_i x^2_{i,\perp}.$$
При этом не нужно вычислять сумму (интеграл), если использовать аналогию с моментом инерции:
$$\sum_i{m_ix^2_{i,\perp}}=\frac{2}{5}mR^2 \implies \sum_i{Q_ix^2_{i,\perp}}=\cfrac{2}{5}QR^2$$
Поэтому суммарный магнитный крутящий момент, действующий на шарик
$$\vec\tau_L=\vec\mu\times\vec B=\cfrac{1}{5}QR^2\times\vec B=\cfrac{Q}{2m}\vec L\times \vec B.$$
Угловое ускорение шарика вызвано моментом силы трения и магнитным крутящим моментом. Как видно из рисунка, оба крутящих момента имеют одинаковое направление, перпендикулярное угловой скорости шарика. В результате ось вращения шарика прецессирует в горизонтальной плоскости. Дл удовлетворения условия чистого качения угловая скорость прецессии должна равняться $\Omega$. В ходе прецессии скорость изменения момента импульса есть $\left|\vec{L}\right|\Omega$, так что уравнение вращательного движения относительно центра шарика:
$$\cfrac{1}{5}QR^2 \omega B+RF=\cfrac{2}{5}mR^2\omega\Omega$$
Здесь $\cfrac{1}{5}QR^2\omega B=\left|\vec\tau_L\right|$, $\cfrac{2}{5}mR^2\omega\Omega=\left|\vec{L}\right|$.
Из уравнений выше можно получить радиус и угловую скорость кругового движения:
$$r=\cfrac{7}{6}\cfrac{mv_0}{QB}, \quad\Omega=\cfrac{6}{7} \cfrac{QB}{m}$$