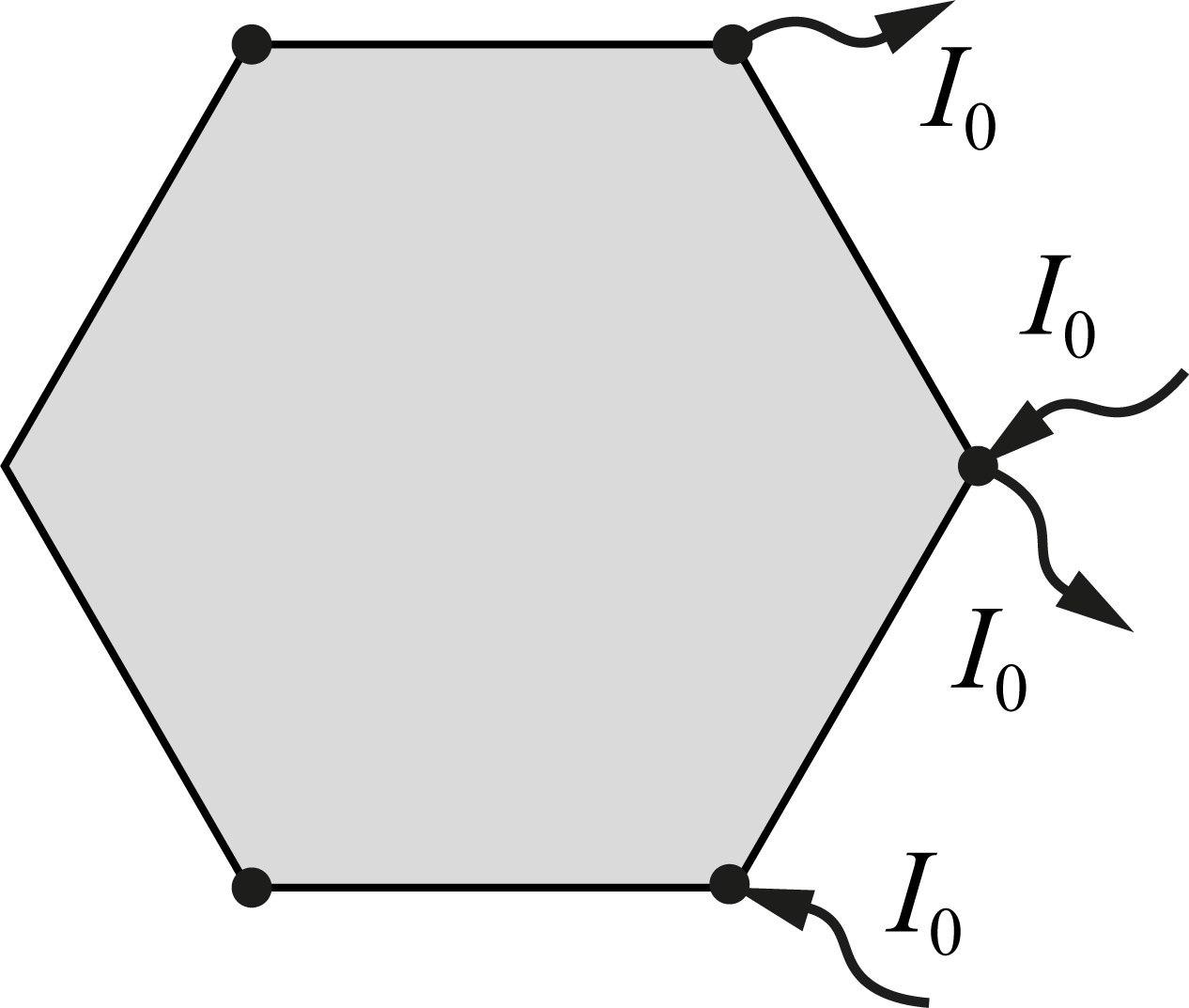
Воспользуемся локальным законом Ома
$$\vec{j}=\frac{\vec{E}}{\rho}
$$
Для определения знаков и отношения проекций электрического поля достаточно найти те же соотношения между проекциями плотностей тока. Для этого воспользуемся методом наложения токов.
Между вершинами $DB$ пропустим силу тока $2I$, между $EA$ — $5I$, и между $BA$ — $8I$.
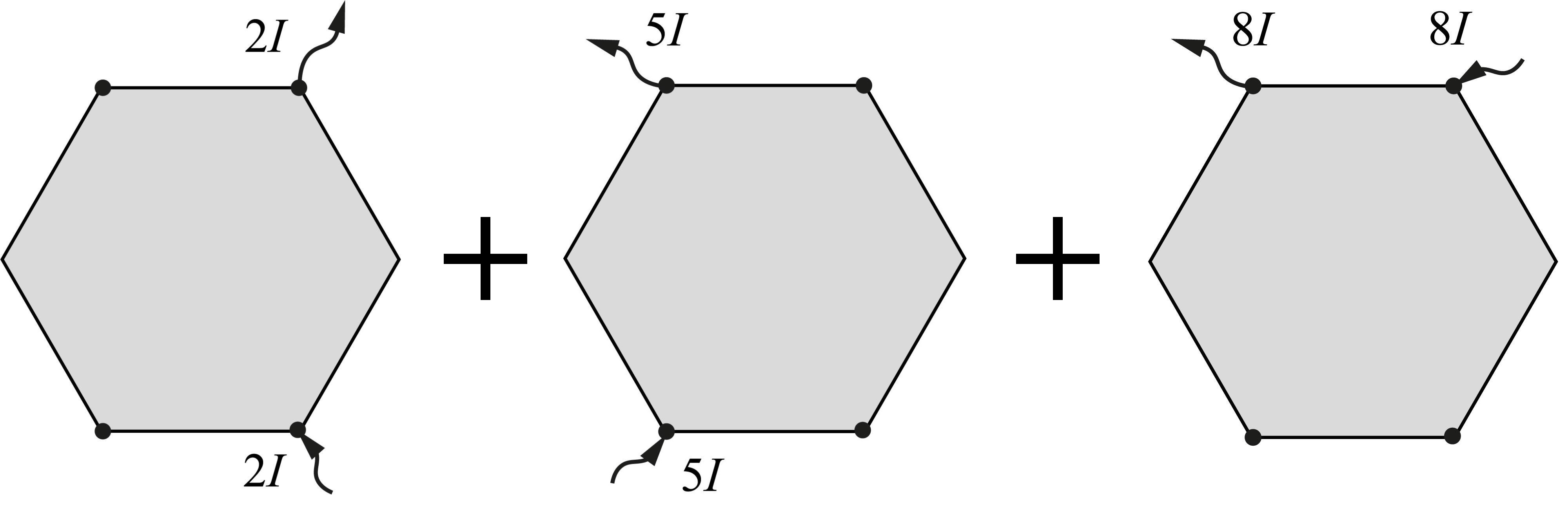
При этом из симметрии ясно, что в первых двух ситуациях $j_y>0$, $j_x=0$ и в третьей ситуации $j_x<0$ и $j_y=0$. Поскольку электрическое поле подчиняется принципу суперпозиции, вектор плотности тока - тоже. Таким образом
$$E_x<0\quad\text{и}\quad E_y>0$$
При подключении источника к двум вершинам линии тока не меняются при увеличении силы тока. Поэтому введём коэффициент пропорциональности модуля плотности тока в центре и силы тока
$$j=kI
$$
При разных подключениях коэффициент $k$ разный. Они одинаковы в первом и втором подключении. Обозначим его за $k_1$. Коэффициент в третьем подключении обозначим за $k_2$. Таким образом
$$\frac{E_x}{E_y}=-\frac{8}{7}\frac{k_2}{k_1}
$$