A1  ^?? Измерьте омметром сопротивление ограничительного резистора $R_1$ (cм. оборудование). Ниже указано его приблизительное значение 10 Ом, однако в расчётах используйте полученное вами более точное значение.

Измерим мультиметром в режиме омметра сопротивление ограничительного резистора $R_1 = 10,1~Ом$.

A2  ^7.50 Экспериментально подтвердите справедливость предложенной модели. Для этого исследуйте ВАХ раствора при 5-ти различных расстояниях между электродами.

Собираем измерительную цепь, состоящую из последовательно включённых батарейки, блока регулировки и шприца с раствором соли. К электродам шприца подключаем вольтметр. Второй вольтметр подключаем параллельно эталонному сопротивлению $R_1$ для измерения силы тока в цепи.

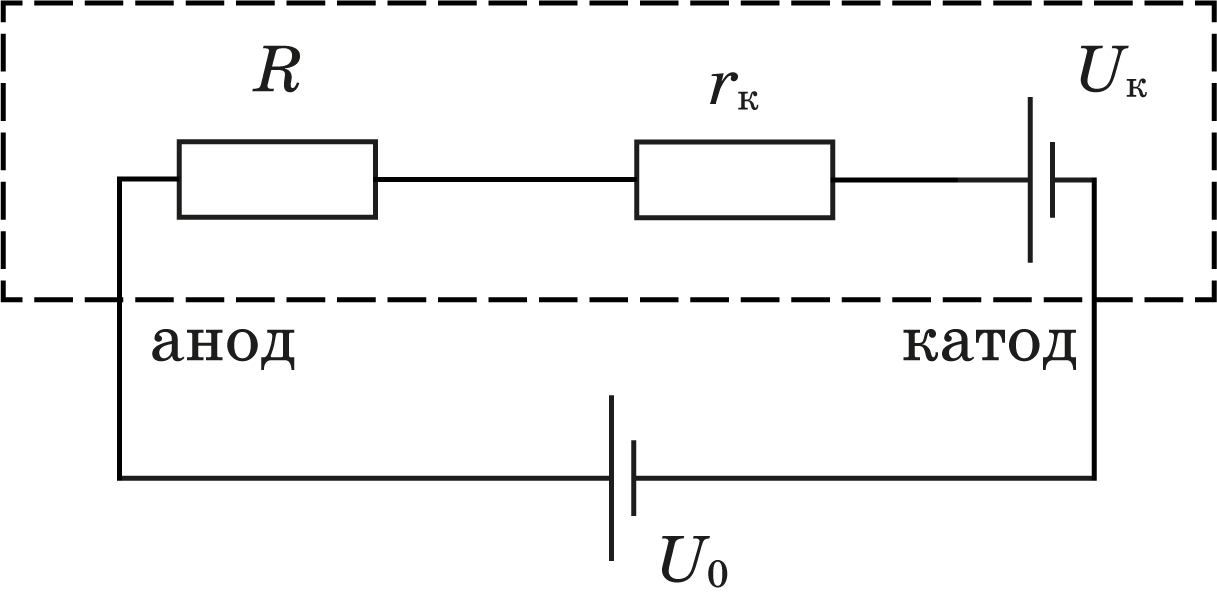
Теоретическая ВАХ электролитической ванны в рамках данной модели имеет вид
$$ I = (U - U_к) / ((\rho L/S) + r_к ) ~~~~~~~(1) $$ где $I$ – сила тока в цепи, и при фиксированной $L$ представляет собой прямую линию, пересекающую ось напряжения в точке $U = U_к$ . Коэффициент наклона этой прямой определяется суммой контактного и объёмного сопротивлений $R_{сум}$ $$(ΔU/ΔI) = (ρL/S) + r_к = R_{сум} ~~~~~~~(2) $$ Зависимость угла наклона ВАХ электролитической ванны от длины ванны $L$ в рамках данной модели, согласно $(2)$, должна быть линейной. График этой зависимости даст возможность при известной $S$ определить величины $ \rho $ и $r_к$ .

Снимаем вольт-амперную характеристику раствора. В таблицах приведены результаты измерения ВАХ раствора при 5 различных объёмах жидкости в шприце $V$ (и соответствующих расстояниях $L$ между электродами).

$U_{10}$ , мВ;$U$, мВ; $I$, мA; $V$, мл;$L$, см 290;1740;28,7;4;1,3 320;1860;31,7 450 ;2060; 44,6 650; 2460; 64,4 770 ;2670 ;76,2 990 ;3080 ;98,0 1080; 3420; 106,9

$U_{10}$ , мВ;$U$, мВ; $I$, мA; $V$, мл;$L$, см 870 ;3750; 86,1;8;2,6 800 ;3570; 79,2 740 ;3340; 73,3 540 ;2920; 53,5 392 ;2300; 38,8 294 ;2040; 29,1 269 ;1970; 26,6

$U_{10}$ , мВ;$U$, мВ; $I$, мA; $V$, мл;$L$, см 254; 2160; 25,1;12;3,9 269 ;2230 ;26,6 330 ;2450 ;32,7 490 ;3100 ;48,5 610 ;3550 ;60,4 670 ;3790 ;66,3 730 ;3950 ;72,3

$U_{10}$ , мВ;$U$, мВ; $I$, мA; $V$, мл;$L$, см 574;4140; 56,8;16;5,2 578 ;4010; 57,2 520 ;3800; 51,5 475 ;3400; 47,0 425 ;3180; 42,1 319 ;2650; 31,6 266 ;2400; 26,3

$U_{10}$ , мВ;$U$, мВ; $I$, мA; $V$, мл;$L$, см 213 ;2600; 21,1;20;6,5 289 ;3070; 28,6 360 ;3410; 35,6 451 ;3950; 44,7 501 ;4150; 49,6 523 ;4250; 51,8

Строим ВАХ для всех экспериментов

A3  ^1.00 Оцените величину контактной разности потенциалов $U_\text{к}$.

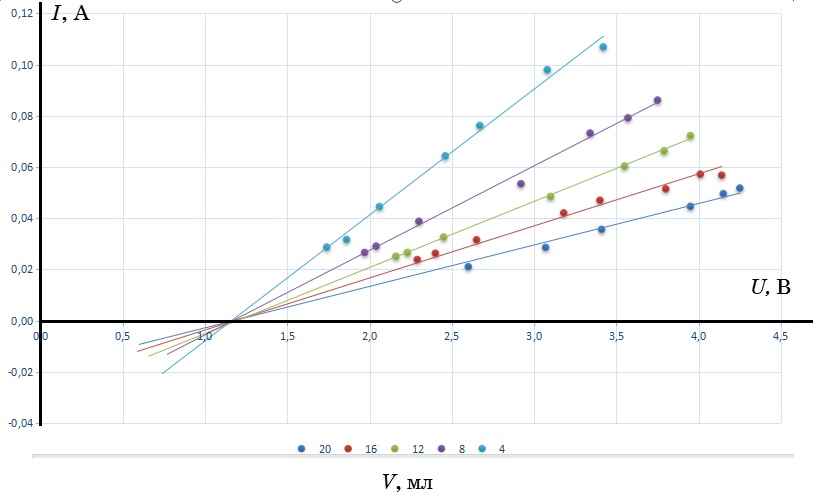
С помощью графика определяем:
1. Из точки пересечения графиков и оси напряжений величину контактной разности потенциалов $U_к = 1,2~В$.
2. Из углового коэффициента (см. формулу $(2)$) сопротивление объёма электролита вместе с сопротивлением контактных областей $R_{сум}$ для 5-ти значений $L$.

A4  ^2.50 Определите величину контактного сопротивления $r_\text{к}$.

Результаты обработки экспериментальных данных для пяти значений $L$ представлены в таблице и на рисунке.

№;$L$, м; $1/R_{сум}$ , 1/Ом; $R_{сум}$ , Ом 1; 0,065; 0,016; 62,5 2; 0,052; 0,020; 50,0 3; 0,039; 0,026; 38,5 4; 0,026; 0,033; 30,3 5; 0,013; 0,049; 20,4

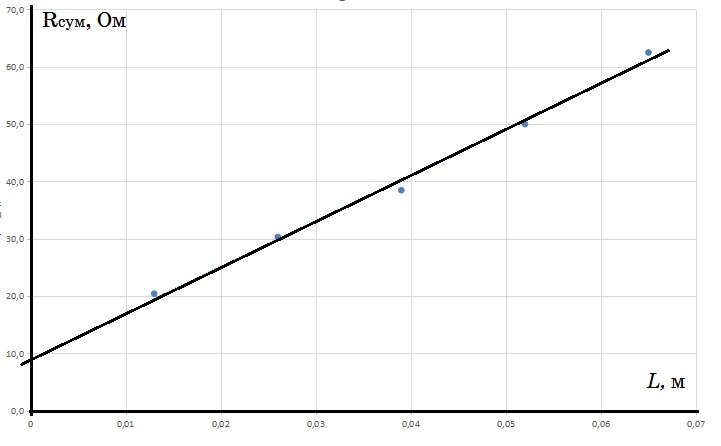
Из графика находим $r_к = R_{сум}(0) = 9,2~Ом$.

A5  ^1.00 Рассчитайте удельную проводимость $\sigma$ трёхпроцентного раствора хлорида натрия в воде.

Площадь сечения поршня $S = 3,1·10^{-4}~м^2$ (можно найти измеряя диаметр поршня или отношение объёма к длине). В рамках используемой модели $ ΔR_{сум}/ΔL = ρ/S$. По наклону прямой графика $R_{сум}(L)$ находим удельное сопротивление используемого раствора соли $ρ = 0,24~ Ом·м$. То есть, $σ = 1/ρ = 4,2 ~(Ом·м)^{-1}$.

A6  ^3.00 Вычислите подвижность $\mu$ ионов натрия и хлора в этом растворе.

Удельная проводимость электролита $σ = 1/ρ = q_1n_1µ_1 + q_2n_2µ_2$ где $q_1$ и $q_2$ модули электрических зарядов положительных и отрицательных ионов соответственно ( в случае ионов натрия и хлора $q_1 = q_2 = е$, где $е$ – элементарный заряд), $n_1$ и $n_2$ – их концентрации ( в нашем случае они одинаковы и равны $n$), $µ_1$ и $µ_2$ - подвижности отрицательных и положительных ионов в растворе, которые, согласно условию задачи, также равны друг другу
$µ_1 = µ_2 = µ$. Окончательно, $$µ=\frac{σ}{2еn}$$

Вычисляем концентрацию ионов натрия (или хлора) в трёхпроцентном растворе поваренной соли $NaCl$ $$n =N/V=\frac{m_{NaCl}N_a\rho_{раств}}{M_{NaCl}m_{раств}}=0,03\frac{N_a\rho_{раств}}{M_{NaCl}}= 3,2·10^{26} ~м^{-3}$$.

Вычисляем подвижность: $$µ = \frac{σ}{(2еn)} = 4,0·10^{-8}\frac{м^2}{В·с}$$, что хорошо согласуется с литературными данными.