A1  ^1.00 Пусть $v(x)$ — скорость течения жидкости в щели. Начало координат оси $Ox$ находится посередине между плоскостями, а плоскости, ограничивающие течение, находятся при $x = \pm d/2$. Разность давлений на противоположных краях щели равна $\Delta P$. Рассматривая силы, действующие на бесконечно малый слой жидкости толщины $dx$, получите дифференциальное уравнение на $v(x)$. Найдите из него $v(x)$. На стенках щели скорость обращается в 0.
Найдите среднюю скорость течения жидкости $\langle v \rangle$ (выразите ее через $\Delta P$, $L$, $\eta$, d). Найдите поток (поток — объем жидкости, протекающий через щель в единицу времени) жидкости через щель. Выразите ответ через $\Delta P$, $L$, $\eta$, $d$, $w$.

Скорость течения жидкости постоянна, поэтому сумма силы давления и силы вязкого трения, действующей на слой жидкости толщины $dx$ должна быть равна нулю, откуда получаем уравнение
$$
\eta \frac{d^2 v}{dx^2}= -\frac{\Delta P}{L},
$$
его решение, удовлетворяющее правильным граничным условиям
$$
v(x) = \frac{\Delta P}{2 \eta L} \left( \frac{d^2}{4} -x^2\right).
$$
Интегрируя, находим среднюю скорость
$$
\langle v \rangle =\frac{1}{d} \int_{-d/2}^{d/2}dx\, v(x) = \frac{\Delta P d^2}{12 \eta L}
$$
и поток
$$
q = dw\langle v \rangle = \frac{d^3 w}{12 \eta L} \Delta P.
$$

A2  ^0.80 Теперь рассмотрим течение жидкости через длинную круглую трубку длины $L$ и радиуса $r$.
Из соображений симметрии скорость при течении через трубку зависит только от расстояния до ее оси. На границе трубки скорость обращается в 0. Найдите зависимость скорости от расстояния до оси $\rho$. Разность давлений на между концами трубки $\Delta P$, вязкость жидкости $\eta$.

Найдите объемный расход $q$ при течении жидкости через трубку. Ответ выразите через $\Delta P$, $L$, $r$, $\eta$.

Приравнивая нулю силу, действующую на цилиндр жидкости радиуса $\rho$, находим уравнение
$$
2 \pi \rho \frac{dv}{d\rho}\eta L = -\pi \rho ^2 \Delta P, \quad
\frac{dv}{d\rho} =- \rho \frac{\Delta P}{2 \eta L}.
$$
Его решение
$$
v(\rho) = \frac{\Delta P}{4 \eta L} (r^2 - \rho^2),
$$
откуда поток равен
$$
q = \int_0^r 2\pi \rho d\rho\, v(\rho) = \frac{\pi r^4 \Delta P}{8 \eta L}.
$$

A3  ^0.20 Найдите гидродинамические сопротивления щели $R_s$ и трубки $R_t$. Ответ выразите через геометрические размеры, заданные в пунктах A1 и A2 соответственно и через вязкость жидкости $\eta$.

Используя результаты предыдущих пунктов, получим

A4  ^0.70 Жидкость вязкости $\eta$ течет по трубке радиуса $r$ и длины $L$ под действием разности давлений $\Delta P$ (как в A2). Найдите мощность сил вязкого трения.

Работа сил вязкого трения равна по модулю и противоположна по знаку работе сил давления (жидкость движется равномерно, поэтому полная работа равна нулю).
Сила давления, действующая на узкий цилиндр жидкости площади $dS$ (ось цилиндра параллельна направлению движения жидкости) равна $F =\Delta P dS $. Соответствующий вклад в мощность $dW = \Delta P dS v$, а полная мощность сил трения
$$
W = -\int \Delta P v dS = - \Delta P q.
$$

$$W =-q\Delta P =-\Delta P^2/R= - \frac{\pi r^4}{8 \eta L}\Delta P^2$$

Альтернативно можно использовать факт, что в бесконечно малом объеме мощность сил вязкого трения $dW = - dV \eta (dv/d\rho)^2$.
Интегрируя по объему, найдем
$$
W = \int dV \eta (dv/d\rho)^2= - \eta L \int_0^r d\rho\, 2\pi \rho (dv/d\rho)^2 = - \frac{\pi r^4}{8 \eta L}\Delta P^2.
$$

B1  ^0.40 Пусть заданы объемные расходы $q_1$ и $q_2$ жидкостей 1 и 2, а также их средние скорости $\langle v_1\rangle$ и $\langle v_2\rangle$. Найдите относительную ширину потока образца $w_1/w$.

Напишем выражения для потоков жидкостей через их средние скорости и ширины потоков:
$$
q_1 = \langle v_1 \rangle d w_1, \quad q_2 = \langle v_2 \rangle d w_2= \langle v_2 \rangle d (w-w_1).
$$
Решая полученные уравнения, находим
$$
\frac{q_2}{q_1} = \frac{\langle v_2 \rangle}{\langle v_1 \rangle}\left( \frac{w}{w_1}-1\right), \quad \frac{w_1}{w} = \frac{1}{1+ q_2 \langle v_1 \rangle/q_1\langle v_2 \rangle}.
$$

B2  ^0.40 Пусть заданы вязкости жидкостей $\eta_1$ и $\eta_2$, а их средние скорости определяются результатами части $A$. Выразите $w_1/w$ через $q_1$, $q_2$, $\eta_1$ и $\eta_2$. Эффектами, которые происходят на границе между жидкостями 1 и 2, можно пренебречь, так как они важны только в области шириной порядка $d \ll w$.

Из формул для средних скоростей
$$
\frac{\langle v_1 \rangle}{\langle v_2 \rangle} = \frac{\eta_2}{\eta_1}
$$

B3  ^0.30 Найдите отношение потоков $q_1/q_2$, если заданы плотности жидкостей ($\rho_1$ и $\rho_2$), их вязкости ($\eta_1$ и $\eta_2$) и высоты, на которые подняты резервуары $h_1$ и $h_2$.

$$
\frac{q_1}{q_2} = \frac{\rho_1 g h_1/R_1}{\rho g h_2/R_2} = \frac{\rho_1 h_1}{\rho_2 h_2} \frac{R_2}{R_1} = \frac{\rho_1 h_1 \eta_2}{\rho_2 h_2 \eta_1 }
$$

B4  ^0.30 Найдите соответствующее отношение ширин потоков $w_1/w$.

C1  ^0.40 Опять рассмотрим течение одной жидкости между плоскостями. Однако теперь скорость создается не только за счет разности давлений, но и за счет силы тяжести. Геометрия такая же как и в части A1, сила тяжести направлена вдоль оси $y$. Поток жидкости сонаправлен с силой тяжести. Найдите среднюю скорость жидкости. Выразите ответ через $\rho$, $g$, $\eta$, $d$, $\Delta P$, $L$.

Без учета гравитации
$$
\langle v \rangle =\frac{ d^2}{12 \eta L} \Delta P.
$$
За счет гравитации возникает дополнительный вклад в разность давлений
$$
\Delta P \to \Delta P + \rho g L.
$$
Отсюда скорость

C2  ^0.80 Пусть теперь между плоскостями течет два типа жидкостей, как в части $B$. Написав выражения для средних скоростей жидкостей 1 и 2, исключите из них разность давлений (она одинакова для обеих жидкостей) найдите отношение $\langle v_1 \rangle / \langle v_2 \rangle$. Выразите ответ через $\langle v_2 \rangle$, $\eta_1$, $\eta_2$, $d$, $g$, $\rho_1$, $\rho_2$.

Запишем выражения для средних скоростей двух жидкостей
$$
\langle v_1 \rangle =\frac{ d^2}{12 \eta_1 } \left(\frac{\Delta P}{L}+ \rho_1 g\right),
\quad
\langle v_2 \rangle =\frac{ d^2}{12 \eta_2 } \left(\frac{\Delta P}{L}+ \rho_2 g\right).
$$
Умножим эти уравнения на соответствующие вязкости и вычтем одно из другого
$$
\eta_1 \langle v_1 \rangle - \eta_2 \langle v_2 \rangle = \frac{gd^2}{12 } (\rho_1 - \rho_2).
$$
Разделив на $\eta_1 \langle v_2 \rangle$ получим
$$
\frac{\langle v_1 \rangle}{\langle v_2 \rangle} - \frac{\eta_2}{\eta_1} = \frac{g d^2}{12 \eta_1 \langle v_2 \rangle} (\rho_1-\rho_2)
$$
откуда

C3  ^1.00 Подставьте выражение для средних скоростей в формулу для относительной ширины сфокусированного потока из B1. Получите уравнение для определения ширины вида
$$\frac{w}{w_1} = \dots$$
В правую часть могут входить отношение $\frac{w_1}{w}$ и безразмерные параметры $\alpha = q_2 \eta_2/q_1 \eta_1$, $\beta = (\rho_1 - \rho_2)q_G/ \rho_2 q_2$. Здесь $q_G= \rho_2 g d^3 w/12\eta_2$ — величина с размерностью потока жидкости, характеризующая влияние гравитации.

Используем соотношение из B1
$$
\frac{w}{w_1}=1+ q_2 \langle v_1 \rangle/q_1\langle v_2 \rangle.$$
Подставим в него найденное ранее отношение скоростей
$$
\frac{w}{w_1}=1+ \frac{q_2 \eta_2}{q_1 \eta_1} \left( 1+\frac{g d^2}{12 \eta_2 \langle v_2 \rangle} (\rho_1-\rho_2) \right).
$$
Выразим среднюю скорость $\langle v_2 \rangle$ через соответствующий поток:
$$
\langle v_2 \rangle = \frac{q_2}{d w_2} = \frac{q_2}{d(w-w_1)}.
$$
Тогда
$$
\frac{w}{w_1}=1+ \frac{q_2 \eta_2}{q_1 \eta_1} \left( 1+\frac{g d^3}{12 \eta_2 q_2} (\rho_1-\rho_2) (w-w_1)\right).
$$
Преобразуем это выражение:
$$
\frac{w}{w_1}=1+ \frac{q_2 \eta_2}{q_1 \eta_1} \left( 1+\frac{g d^3 w}{12 \eta_2 q_2} (\rho_1-\rho_2) \frac{w-w_1}{w}\right) =
$$
$$
1 + \alpha \left( 1+ \frac{q_G (\rho_1 - \rho_2)}{q_2 \rho_2}\left(1- \frac{w_1}{w}\right)\right) = 1+ \alpha \left( 1+ \beta \left(1- \frac{w_1}{w} \right)\right).
$$

C4  ^0.60 Решите это уравнение и найдите относительную ширину сфокусированного потока $w_1/w$. Ответ выразите через безразмерные величины $\alpha$, $\beta$.

Получили квадратное уравнение
$$
\alpha \beta\frac{w_1^2}{w^2} - (1 + \alpha + \alpha \beta)\frac{w_1}{w} +1 = 0.
$$
Его решение (нужный нам корень должен быть меньше 1, поэтому берем знак -)

D1  ^0.60 Найдите гидродинамическое сопротивление каждого из реостатов, если по ним течет вода. Пусть в качестве жидкости 1 используется раствор соли, плотность которого $\rho_1 = 1.15 \cdot 10^3~кг/м^3$, а вязкость совпадает с вязкостью воды. Найдите $q_G$ для такой щели.

Подставляем приведенные выше числа в формулы для сопротивления и $q_G$
$$
R = \frac{8 \eta L}{\pi r^4}, \quad q_G = \frac{\rho_2 g d^3 w}{12 \eta_2}
$$

D2  ^0.30 Найдите относительную ширину потока жидкости 1 (раствора соли)
$w_1/w$ для случаев, когда жидкость 1 подается с высот $h_1 = 0.25~м,\, 0.5~м,\,1.0~м$.

Подставим числа в формулы, полученные в C4. Подставим числа в формулы из B4. Получим значения для $h= 0.25~м, \,0.5~м, \,1.0~м$ соответственно:

D3  ^0.30 Как изменится значение ширины потока, если пренебречь влиянием силы тяжести? Вычислите относительную ширину потока для тех же параметров $h_1 = 0.25~м,\, 0.5~м,\,1.0~м$, что и в предыдущем пункте, не учитывая силу тяжести.

Подставим числа в формулы из B4. Получим значения для $h= 0.25~м, \,0.5~м, \,1.0~м$ соответственно:

D4  ^0.30 Пусть теперь по центру течет некоторая жидкость 1, плотность которой равна $\rho_1^\prime = 0.8 \cdot 10^3 кг/м^3$, а вязкость совпадает с вязкостью воды.
Найдите отношение $w_1/w$ для значений $h_1 = 0.25~м,\, 0.5~м,\,1.0~м$.

D5  ^0.80 Постройте качественно на одном графике зависимости $w_1/w$ от $h_2/h_1$ для трех случаев: a) гравитации нет, b) по центру течет раствор соли, c) по центру течет жидкость с плотностью $\rho_1^\prime$. Все параметры как в предыдущих пунктах, высота $h_2$ фиксирована, меняется только $h_1$.

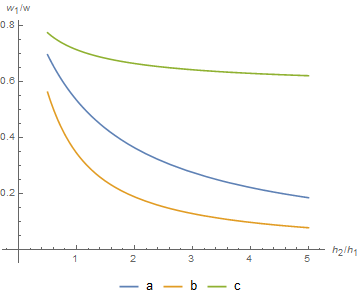
На рисунке приведены графики для случаев a), b), c) соответственно. Обратите внимание, что все три зависимости монотонно убывают, а также на порядок расположения кривых (когда плотность центральной жидкости больше, поток становится уже после учета гравитации, а когда меньше — поток наоборот расширяется).

D6  ^0.80 Во всех расчетах мы предполагали, что потоки не зависели от времени.
Пусть резервуар для воды (жидкости 2) представляет собой цилиндр радиуса $r_r = 20~мм$.
Оцените время, за которое уровень воды в резервуаре уменьшается на $\delta h_2 = 10~см$. Если эксперимент провести за время такого порядка, изменение уровня воды в резервуаре практически на нем не скажется. Начальный уровень равен $h_2 = 0.5~м$.

Скорость уменьшения уровня воды можно оценить из
$$
\pi r_r^2 \frac{dh_2}{dt} = -q_2 = -\frac{\rho_2 g h_2}{R}.
$$
Считая эту скорость приближенно постоянной, находим