
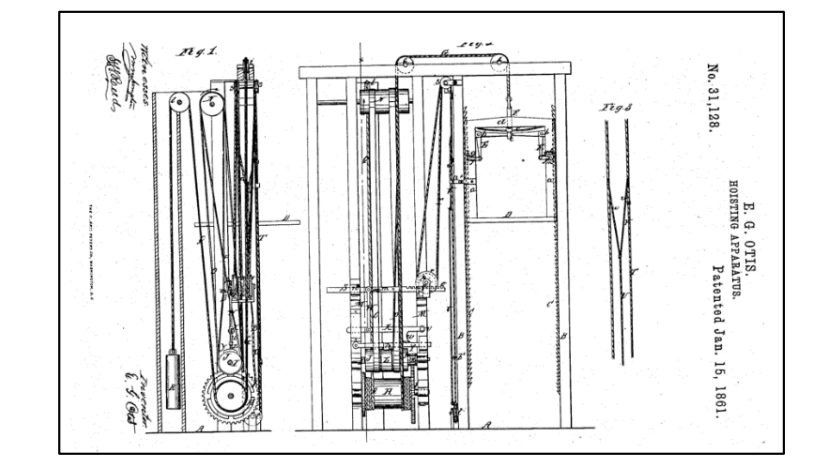
В 1854 году на Всемирной выставке в Нью-Йорке Элиша Отис под аплодисменты публики впервые продемонстрировал механизм страховки своего лифта. Элиша поднялся на лифте на высоту четвертого этажа, а его помощник тем временем отрезал трос, который держал лифт — все это пока сам Элиша находился внутри лифта!
К счастью, механизм страховки сработал и лифт остановился после короткого падения. Механизм страховки таким образом несколько раз подряд спас жизнь своего изобретателя.
В этой задаче мы рассмотрим два механизма страховки лифтов.
Та часть, которую столь драматически демонстрировали на выставке, являлась экстренным тормозом.
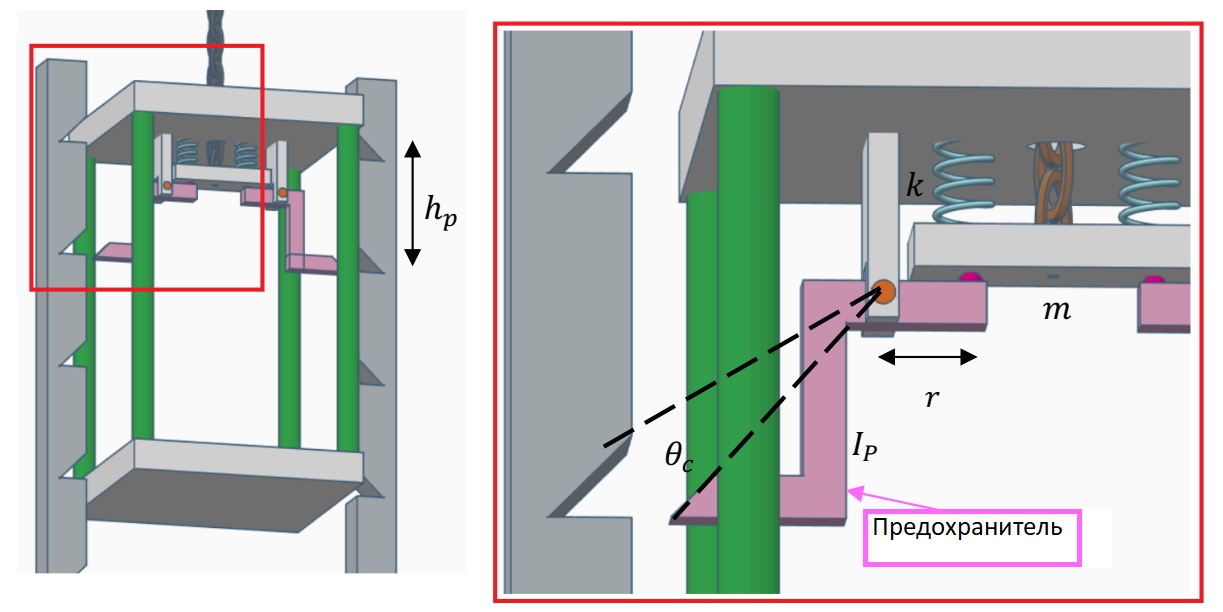
Принцип действия механизма:
В нормальном состоянии трос, который держит лифт, сильно натянут и сжимает две пружины (каждая с коэффициентом упругости $k=30~\text{кН/м}$).
Когда трос отрезан, пружины освобождаются и балка весом $m = 10 ~\text{кг}$, опускается вниз относительно лифта. Она, в свою очередь, заставляет предохранители повернуться так, что их концы встают в углубления в рельсах по обе стороны лифта. Углубления расположены на одинаковом расстоянии $h_p=0.15~\text{м}$ по всей высоте рельсов. Момент инерции каждого предохранителя (относительно оси вращения) $I_p=3~\text{кг}\cdot\text{м}^2$. Расстояние от оси до точки давления на предохранители со стороны балки $r=0.3~\text{м}$ Для того чтобы предохранитель пришёл в углубление напротив, он должна провернуться на угол $ \theta =6 ^{\circ} $ от изначального состояния.
Если предохранитель был бы повернут на угол $12^{\circ}=2\theta~\ll~90^{\circ}$, то пружины были бы полностью нерастянуты.
Масса пустого лифта $M=300~\text{кг}$, а масса Отиса вместе с его пожитками $m_1=200~\text{кг}$.
Ускорение свободного падения $g=10~\text{м/с}^2$.
A2
1.50
Рассмотрим другую ситуацию: трос не перерезается, но передача от него к двигателю ломается. Это приводит к тому, что сила натяжения меньше, чем сила, удерживающая лифт в состоянии покоя. Каково максимальное ускорение $a_1$, с которым лифт будет падать вниз в такой ситуации? (Отис все еще внутри).
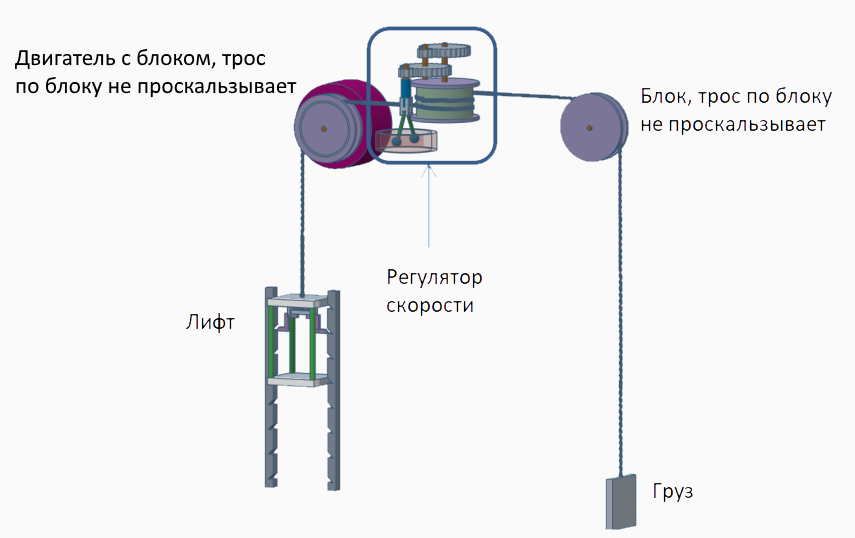
Из предыдущих пунктов ясно, что лифт следует снабдить дополнительными средствами защиты от падения с большой скоростью. Регулятор скорости и есть тот механизм, который предоставит соответствующую защиту.
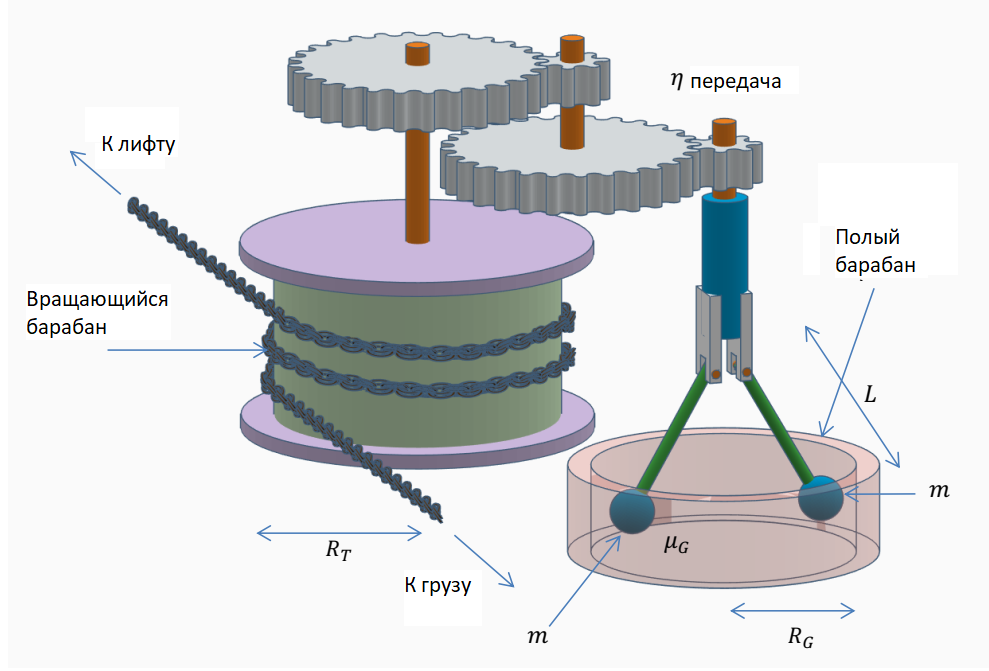
Ниже данные для параметров изображенных на рисунке:
$R_T=1.1~\text{м},~R_G=0.4~м,~\mu_G=0.3,~L=0.5\text{м},~m=12~\text{кг},~\eta=6.$
Регулятор скорости состоит из нескольких частей:
— Вращающийся барабан , на который наматывается трос. С одной стороны на тросе подвешен лифт, а с другой - уравновешивающий груз. Барабан очень шершавый так что нет проскальзывания между ним и тросом.
— Передача с передаточным отношением $\eta$, которая связывает вращающийся барабан с быстро вращающейся осью.
— Быстро вращающаяся ось, на ней шарнирно закреплены два штифта (стержня) с грузами на нижних концах.
Штифты могут откидываться от оси в зависимости от угловой скорости, с которой они движутся.
— Полый барабан внутри которого вращаются штифты.
Передача создает ситуацию, при которой грузы движутся с большей угловой скоростью, чем скорость вращения вращающегося барабана. Скорость достаточно высока, для того чтобы грузы раскрывались и касались внутренних стенок барабана и трение между грузами и барабаном способно регулировать скорость лифта, чтобы она не была слишком большой.
Современные лифты предназначены для работы с наименьшим, насколько это возможно, потреблением электроэнергии. Исследуем потребление энергии лифтом в современном офисном здании.
Высота здания $H=43~\text{м}$.
Масса пустого лифта $M_E=800~\text{кг}$, дополнительно лифт способен нести максимум $M_{max}=1200~\text{кг}$.
Номинальная скорость движения лифта $\upsilon=1.25~\text{м/c}$, номинальное ускорение лифта $a=1.0~\text{м/c}^2$ Масса уравновешивающего груза $M_c=1300~\text{кг}$.
КПД электрического двигателя лифта $\eta=0.83$.
Часть времени, когда лифт движется в течение суток $D=10\%$.
Для простоты примем что половину времени лифт едет полностью загруженный, а половину времени — пустой. За каждую поездку лифт проезжает всю высоту здания, количество подъемов равно количеству спусков.
В этой модели лифт работает исключительно как потребитель энергии, то есть торможение он производит с помощью тормозов, которые превращают всю кинетическую энергию от движения лифта в тепло. Также, когда лифт спускается полным, двигатель не поставляет электричество, но тормоза должны работать и во время спуска.
Средний тариф за электричество: $\frac{C}{E}=6~\frac{\text{руб}}{\text{кВт}\cdot \text{ч}}$.
Для того чтобы уменьшить эти расходы, можно приобрести лифт с системой аккумуляции энергии (например с батареей, маховым колесом, суперконденсаторами), которые позволят тратить меньше энергии. В такой системе электрический двигатель, который приводит лифт в движение будет выступать в качестве генератора в ситуации, когда механическая энергия лифта уменьшается (например когда лифт спускается при полной загрузке). КПД генератора равен КПД электрического двигателя: $\eta_{gen}=\eta=0.83$.