Pho.rs: Двухкомпонентные смеси

A1 ^1.00 Дано $p_A$, $p_B$, $x_A$ , $x_B$. Найти молярные доли компонент смеси в газообразной фракции ($y_A$ и $y_B$).

A1. 1 $$
y_A = \frac{{p_A x_A} }{ {p_A x_A+p_B x_B}} \\
y_B = \frac{{p_B x_B} }{ {p_A x_A+p_B x_B}} \\
$$

1.00

A2 ^0.50 Пусть для жидкости известны молярная теплота парообразования $\lambda$ и температура кипения жидкости $t$ при атмосферном давлении $P_0$. Найдите зависимость давления насыщенного пара чистой жидкости от температуры $P(T)$.

A2. 1 $$
P = P_0 e^{\frac{\lambda}{ R}(\frac{1 }{ t}-\frac{1}{T})}
$$

0.50

A3 ^1.00 Выразите $p_A/p_B$ при температуре $T$ через температуры кипения чистых жидкостей $t_A$ и $t_B$ (при атмосферном давлении), их молярные теплоты парообразования $\lambda_A$ и $\lambda_B$.

A3. 1 $$
\frac{p_A }{ p_B} (T) = e^{\frac{\lambda_A }{ R} (\frac{1 }{ t_A}-\frac{1 }{ T}) - \frac{\lambda_B }{ R} (\frac{1 }{ t_B}-\frac{1 }{ T})}
$$

1.00

A4 ^2.00 Считая $\lambda_A=\lambda_B=\lambda$, найдите температуру кипения двухкомпонентной смеси: $T(\lambda,t_A,t_B,x_B)$.

A4. 1 Начальное уравнение: $$ P_0 = P_0 e^{\frac{\lambda_A }{ R} (\frac{1 }{ t_A}-\frac{1 }{ T})} x_A + P_0 e^{\frac{\lambda_B }{ R} (\frac{1 }{ t_B}-\frac{1 }{ T})} x_B $$ Error propagation , если неправильно A2. Обязательно должны быть учтены молярные доли веществ в формуле.	1.00
A4. 2 $$ T = \frac{\lambda }{ R} \ln^{-1} ({x_B e^\frac{\lambda }{ {Rt_B}}+(1-x_B)e^\frac{\lambda }{ {Rt_A}}}) $$	1.00

A5 ^1.50 Считая температуру двухкомпонентной системы $T$ постоянной, изобразите на графиках зависимости $P(x_B) , P(y_B)$ и $y_B(x_B)$.

A5. 1

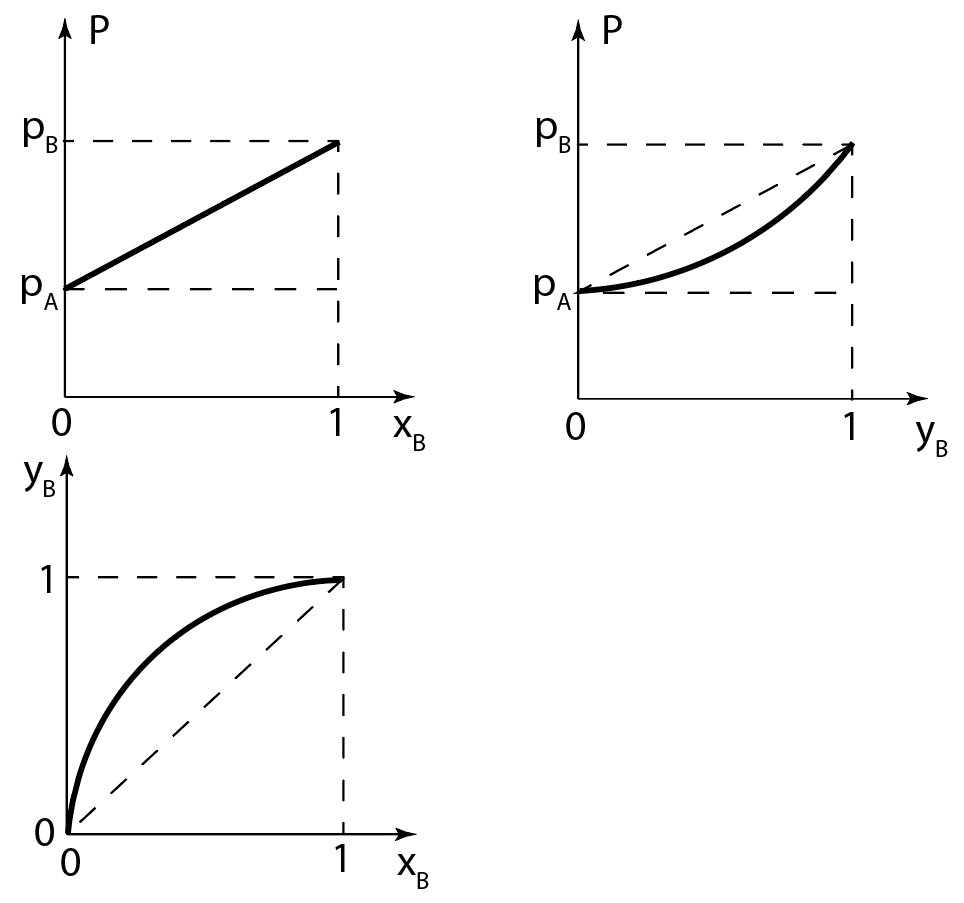
3 × 0.50

A6 ^0.60 Какая $x_B$ будет достигнута после первой конденсации ($N=1$)?

A6. 1 $$ x_B \approx 0.02
$$

0.60

A7 ^1.40 Какая $x_B$ будет достигнута после того как процедура повторится $N=10$ раз, $N= 10^6$?

A7. 1 $$ \frac{{1-x_B(N)}}{{x_B(N)}} = {(\frac{p_A}{p_B})^N} \frac{{1 - x_B(0)}}{{x_B(0)}} $$	0.60
A7. 2 $$ x_B \approx 0.91 $$	0.40
A7. 3 $$ x_B \approx 1.00 $$	0.40

A8 ^2.00 Найдите, во сколько раз к этому моменту уменьшилось общее количество жидкости?

A8. 1 $$ d(x_B V n_L) = -dv \frac{{p_B x_B}}{{RT} } \\ d(x_A V n_L) = -dv \frac{{p_A x_A}}{{RT} } $$ Формулы должны учитывать, что количество уходящего вещества пропорционально парциальному давлению его пара, и не содержать физических ошибок	0.50
A8. 2 $$ \frac{dV }{ V} = \frac{dx_B }{ x_B} + \frac{{2 dx_B} }{ {1-x_B}} $$ Балл ставится, если формула приведена к интегрируемому виду (в нужных переменных)	1.00
A8. 3 $$ V \approx 0.38 V_0 $$	0.50

Двухкомпонентные смеси

Разбалловка