A1  ^1.00 Дано $p_A$, $p_B$, $x_A$ , $x_B$. Найти молярные доли компонент смеси в газообразной фракции ($y_A$ и $y_B$).

По закону Рауля:
$$
P_A = p_A x_A \\
P_B = p_B x_B
$$

По закону Дальтона:
$$
\frac{y_A}{y_B } = \frac{P_A}{P_B}
$$

Следовательно,
$$
\frac{y_A}{y_B } = \frac{ p_A x_A }{ p_B x_B}
$$

A2  ^0.50 Пусть для жидкости известны молярная теплота парообразования $\lambda$ и температура кипения жидкости $t$ при атмосферном давлении $P_0$. Найдите зависимость давления насыщенного пара чистой жидкости от температуры $P(T)$.

Уравнение Клапейрона-Клаузиуса (в случае идеального газа):
$$
\frac{dP }{ dT} = \frac{\lambda }{ {T \Delta v}} = \frac{\lambda P }{ RT^2}
$$

После интегрирования, получим:
$$
P(T) = P_0 e^{\frac{\lambda }{ R} (\frac{1 }{ t}-\frac{1 }{ T})}
$$

A3  ^1.00 Выразите $p_A/p_B$ при температуре $T$ через температуры кипения чистых жидкостей $t_A$ и $t_B$ (при атмосферном давлении), их молярные теплоты парообразования $\lambda_A$ и $\lambda_B$.

$$
p_A(T) = P_0 e^{\frac{\lambda_A }{ R} (\frac{1 }{ t_A}-\frac{1 }{ T})} \\
p_B(T) = P_0 e^{\frac{\lambda_B }{ R} (\frac{1 }{ t_B}-\frac{1 }{ T})}
$$

$$
\frac{p_A }{ p_B} (T) = e^{\frac{\lambda_A }{ R} (\frac{1 }{ t_A}-\frac{1 }{ T}) - \frac{\lambda_B }{ R} (\frac{1 }{ t_B}-\frac{1 }{ T})}
$$

A4  ^2.00 Считая $\lambda_A=\lambda_B=\lambda$, найдите температуру кипения двухкомпонентной смеси: $T(\lambda,t_A,t_B,x_B)$.

При температуре кипения смеси
$$
P = p_A x_A + p_B x_B = P_0
$$

$$
P_0 = P_0 e^{\frac{\lambda_A }{ R} (\frac{1 }{ t_A}-\frac{1 }{ T})} x_A + P_0 e^{\frac{\lambda_B }{ R} (\frac{1 }{ t_B}-\frac{1 }{ T})} x_B \\
1= e^{\frac{\lambda_A }{ R} (\frac{1 }{ t_A}-\frac{1 }{ T})} (1-x_B) + e^{\frac{\lambda_B }{ R} (\frac{1 }{ t_B}-\frac{1 }{ T})} x_B
$$

$$
T = \frac{\lambda }{ R} \ln^{-1} ({x_B e^\frac{\lambda }{ {Rt_B}}+(1-x_B)e^\frac{\lambda }{ {Rt_A}}})
$$

A5  ^1.50 Считая температуру двухкомпонентной системы $T$ постоянной, изобразите на графиках зависимости $P(x_B) , P(y_B)$ и $y_B(x_B)$.

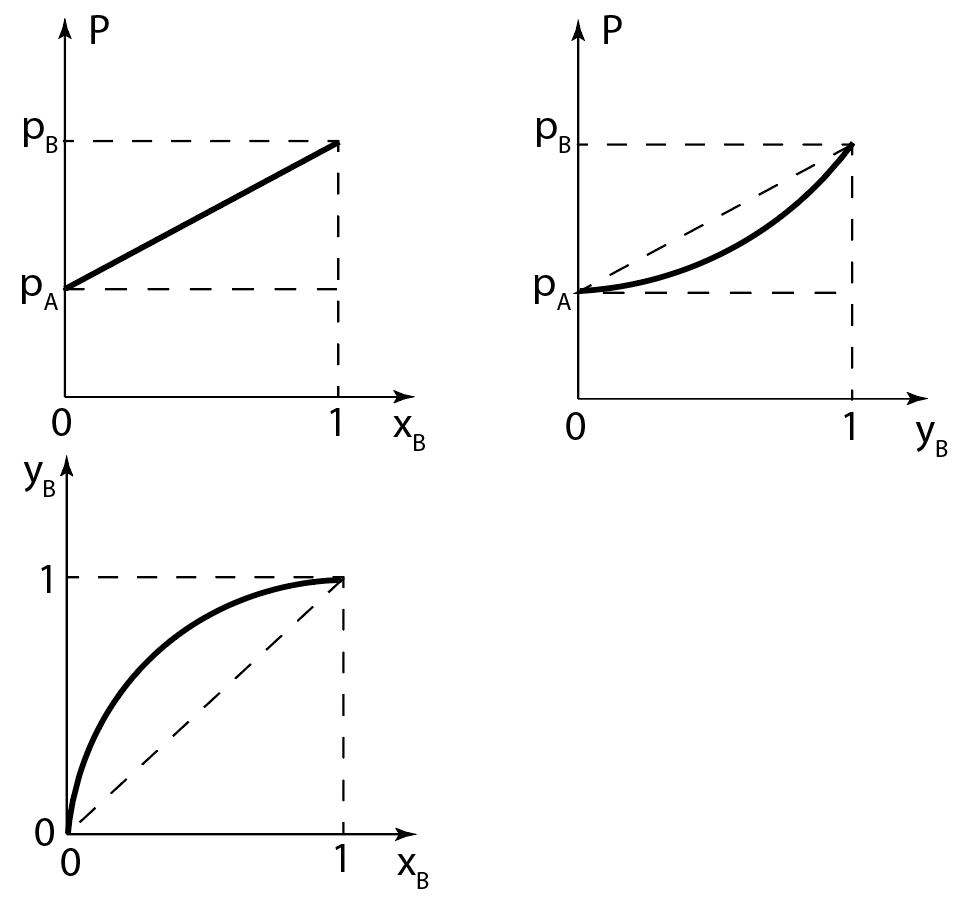
По закону Рауля $P(x_B)$ линейно.
В граничных точках $ x_B=0 , y_B=0 , P = p_A$ или $ x_B=1 , y_B=1 , P = p_B$ .
При $ p_B > p_A $ : $\\$ $ y_B > x_B $.

A6  ^0.60 Какая $x_B$ будет достигнута после первой конденсации ($N=1$)?

$$
x_B (N+1) = y_B(N) \\
\frac{{1-y_B(N)} }{ y_B(N)} =\frac{p_A }{ p_B} \frac{{1-x_B(N)} }{ x_B(N)}
$$

$$
x_B(1) \approx 0.02
$$

A7  ^1.40 Какая $x_B$ будет достигнута после того как процедура повторится $N=10$ раз, $N= 10^6$?

$$
\frac{{1-x_B(N)} }{r x_B(N)} = {(\frac{p_A}{p_B})}^N \frac{{1-x_B(0)}}{x_B(0)}
$$

$$
x_B(10) \approx 0.91 \\
x_B(10^6) \approx 1.00
$$

A8  ^2.00 Найдите, во сколько раз к этому моменту уменьшилось общее количество жидкости?

Рассмотрим уменьшение количества веществ A и B при удалении объема пара $\Delta v$:

$$
dA = - \Delta v \frac{P_A}{{RT}} = - \Delta v \frac{{p_A x_A} }{ {RT}} \\

dB = - \Delta v \frac{P_B }{{RT}} = - \Delta v \frac{{p_B x_B} }{ {RT}} \\

A = x_A n_L V \\
B = x_B n_L V
$$

$n_L$ - молярная плотность жидкости.

Избавляемся от $\Delta v$:
$$
\frac{dA }{ dB} = \frac{{p_A x_A} }{ {p_B x_B}}
$$

Подставляем
$$
dA = dx_A n_L V + x_A n_L dV \\
dB = dx_B n_L V + x_B n_L dV
$$.

После упрощения:

$$
\frac{dV }{ V} = \frac{dx_B }{ x_B} + \frac{{2 dx_B} }{ {1-x_B}}
$$

Интегрируем:

$$
\ln(V/V_0) = \ln(\frac{x_B }{ x_B(0)}) -2 \ln(\frac{{1-x_B}}{ {1-x_B(0)}})
$$

$$
V \approx 0.38 V_0
$$