
Ускорение танка, движущегося с постоянной скоростью $v$, равно $a = \dfrac{v^2}{R}$ и в любой точке траектории направлено вдоль наклонной плоскости к центру окружности.
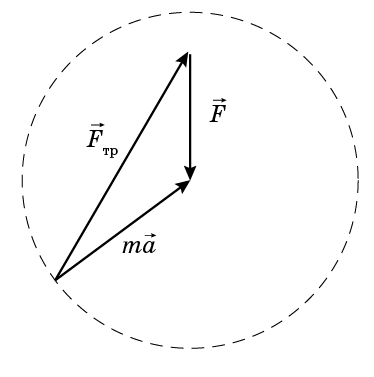
В плоскости, в которой происходит движение, лежат: вектор силы трения покоя (гусеницы не проскальзывают) $F_{тр}$, вектор $ma$ и $F = mg\sin\alpha$ – составляющая вектора силы тяжести вдоль плоскости. В перпендикулярном к плоскости направлении на танк действует сила нормальной реакции $N = mg\cos\alpha$.
Сила трения покоя может принимать любое значение из интервала
$$ 0 \lt F_{тр} \lt \mu mg\cos\alpha.$$
Чтобы время движения танка было минимальным, он должен двигаться с максимально возможной скоростью. Но при больших скоростях силы трения может не хватать для движения с нужным ускорением.
Выразим силу трения из второго закона Ньютона:
$$ \vec{F}_{тр} = m\vec{a} - \vec{F}. $$
Из полученной формулы следует, что модуль разности векторов $m\vec{a}$ и $\vec{F}$ максимален, когда эти векторы направлены противоположно, т.е. в нижней точке траектории. Следовательно, танк сможет пройти всю траекторию с постоянной скоростью $v$, если выполнится условие:
$$ m\dfrac{v^2}{R} \leqslant \mu mg\cos\alpha - mg\sin\alpha, $$
которое и определяет максимальную скорость:
$$ v_{max} = \sqrt{gR(\mu\cos\alpha - \sin\alpha)},$$
и минимальное время движения танка по окружности:
Разумеется, все это справедливо при $\mu \gt tg~\alpha$, в противном случае без проскальзывания танк не смог бы даже стоять на месте.
Найдем максимальный угол между вектором силы трения и ускорения танка. Поскольку вектор $m\vec{a}$ имеет фиксированную величину, но разное направление в разных точках траектории, а вектор $\vec{F}$ – фиксированную величину и направление, то геометрически формула
$$ \vec{F}_{тр} = m\vec{a} - \vec{F} $$
означает, что концы векторов сил трения лежат на окружности с радиусом, равным модулю вектора $m\vec{a}$, а их начала находятся в точке, которая сдвинута на величину $\vec{F}$ по отношению к центру этой окружности (см. рисунок; показано вычитание только одной пары векторов).
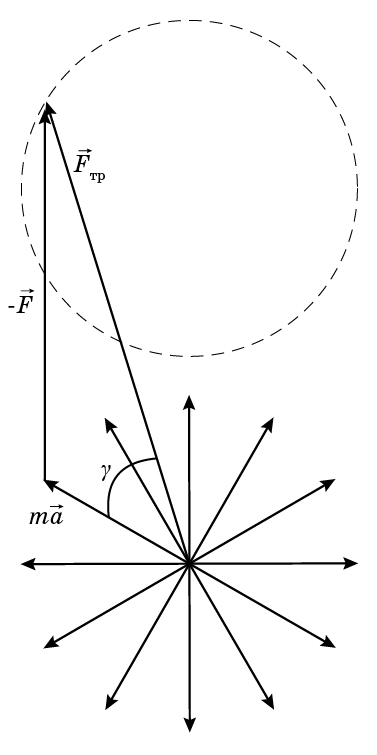
Как следует из рисунка, может реализовываться два варианта.
1) Если модуль силы $\vec{F}$ больше модуля вектора $m\vec{a}$ или
$$ mg\sin\alpha \gt mg(\mu \cos\alpha - \sin\alpha) \Rightarrow \mu \lt 2tg~\alpha \text{(малое трение)},$$
сдвиг окружности, на которой лежат концы вектора силы трения, больше ее радиуса (именно этот случай показан на рисунке), и угол $\gamma$ между вектором силы трения и вектором $m\vec{a}$ (отмечен дугой на рисунке) изменяется от $\gamma = 0^\circ$ (векторы $m\vec{a}$ и силы $\vec{F}$ сонаправлены) до $\gamma = 180^\circ$ (векторы $m\vec{a}$ и силы $\vec{F}$ направлены противоположно).
Если же модуль силы $\vec{F}$ меньше модуля вектора $m\vec{a}$, или
$$mg\sin\alpha \lt mg(\mu \cos\alpha - \sin\alpha) \Rightarrow \mu \gt 2tg~\alpha \text{(большое трение)}, $$
то и в случае сонаправленных векторов $m\vec{a}$ и $\vec{F}$, и в случае противоположно направленных, угол между векторами $m\vec{a}$ и $\vec{F}$ равен нулю, и, следовательно, существует максимальный угол между этими векторами (вычитание векторов $m\vec{a}$ и $\vec{F}$ выполнено на рисунке).
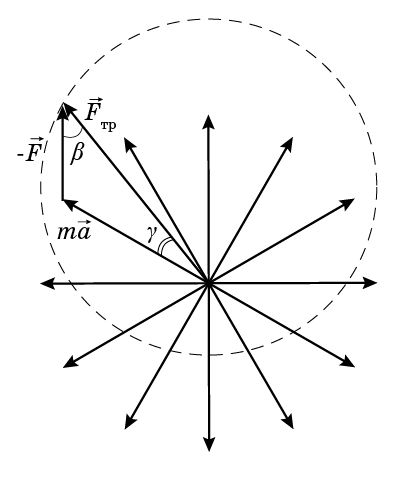
Для нахождения этого угла можно применить теорему синусов к треугольнику сил:
$$ \dfrac{F}{\sin\gamma} = \dfrac{ma}{\sin\beta}, $$
где $\beta$ – угол между вектором силы трения и вектором $-\vec{F}$ (см. рисунок). Поскольку модули векторов $m\vec{a}$ и $\vec{F}$ неизменны во всех точках траектории, то угол $\gamma$ максимален, когда максимален синус угла $\beta$, т.е. $\beta = 90^\circ$. В этом случае синус максимального угла между векторами силы трения и ускорения равен: