Будем решать задачу формально, выразим температуру из модельной функции и запишем сумму $S$, которую нужно минимизировать.
$$T=\frac{\left(p+a_{0}\right) V}{R}$$
$$S=\sum_{n}\left(T_{i}-\frac{p V_i}{R}-\frac{a_{0} V_{i}}{R}\right)^{2}$$
Дифференцируем:
$$\frac{\partial S}{\partial a_{0}}=\sum_{n} 2\left(T_{i}-\frac{\left(p+a_{0}\right) V_{i}}{R}\right)\left(-\frac{V_{i}}{R}\right)=0$$
Преобразуем (сократив на "-2"):
$$\frac{1}{R} \sum_{n} T_{i} V_{i}-\frac{p+a_{0}}{R^{2}} \sum_{n} V_{i}^{2}=0$$
И далее
$$p+a_{0}=\frac{R \sum_{n} T_{i} V_{i}}{\sum_{n} V_{i}^{2}}$$
Окончательно получаем
$$a_{0}=\frac{R \sum_{n} T_{i} V_{i}}{\sum_n V_{i}^{2}}-p=R \frac{\overline{T V}}{\overline{V^{2}}}-p$$

$\textit{Примечание:}$ Ответ можно было бы написать почти сразу, если осознать, что модельная формула — это линейная зависимость с одним параметром: угловым коэффициентом.

$\sum_{n} T_{i} V_{i}=6.5903~К\cdot м^3, \overline{T V}=0.31382~К\cdot м^3$

$\sum_n V_{i}^{2}=1.8935\cdot 10^{-5}~м^6, \overline{V^{2}}=9.0167\cdot10^{-7}~м^6$

Здесь и далее сохраняем побольше значащих цифр для уменьшения погрешности округления итогового ответа.

$a_0=892~кПа$

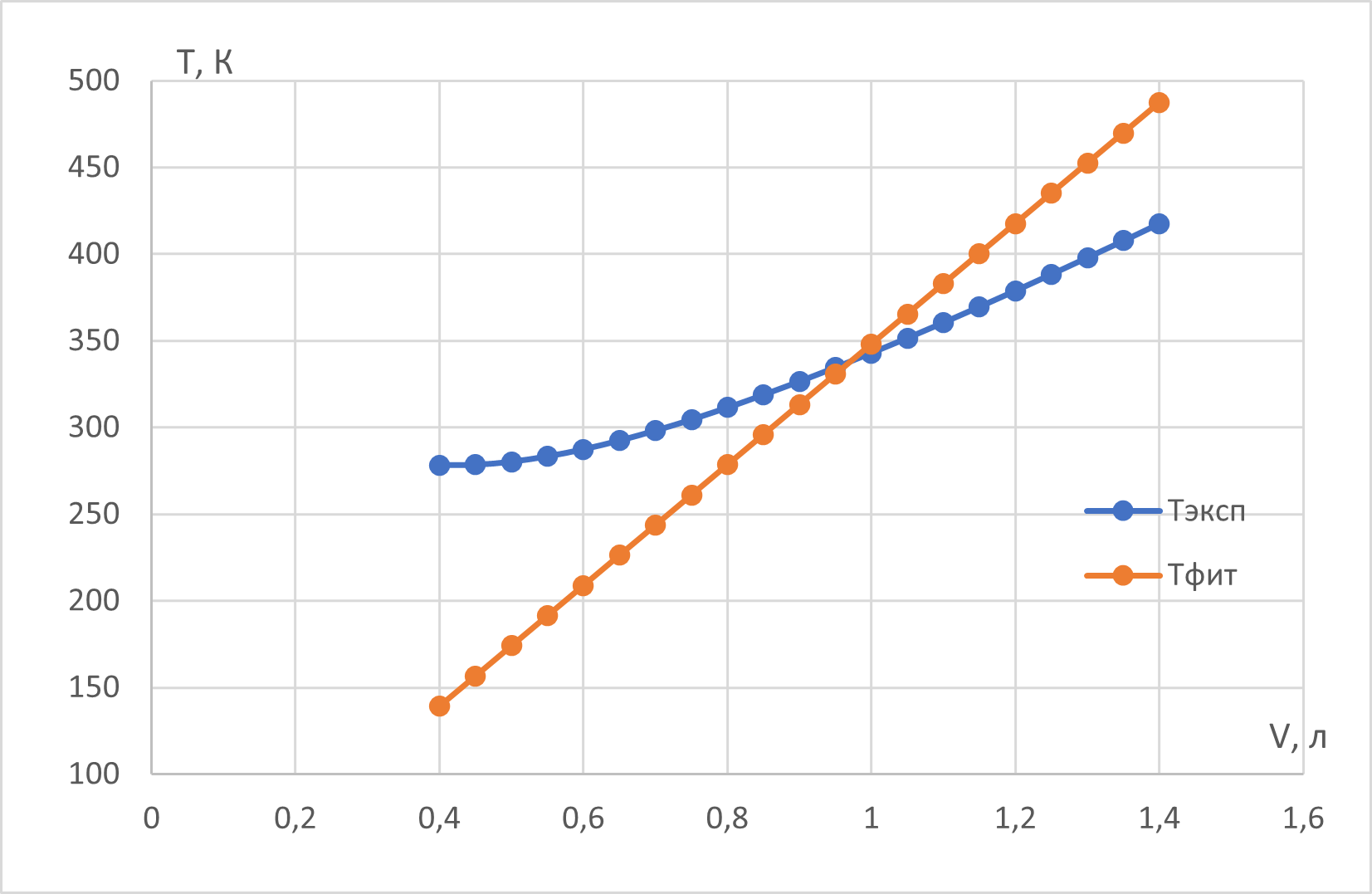
Действуем опять же формально:
$$T=\frac{p V}{R}+\frac{a_{1}}{R}$$
$$S=\sum_{n}\left(T_{i}-\frac{p V_{i}}{R}-\frac{a_{1}}{R}\right)^{2}$$
$$\frac{\partial S}{\partial a_{1}}=\sum_{n} 2\left(T_{i}-\frac{p V_{i}}{R}-\frac{a_{1}}{R}\right)\left(-\frac{1}{R}\right)=0$$
$$\sum_{n} T_{i}-\frac{p}{R} \sum_{n} V_{i}-\frac{a_{1}}{R} \sum_{n} 1=0$$
Откуда получаем окончательный ответ:
$$a_{1}=\frac{R \sum_{n} T_{i}-p \sum_{n} V_{i}}{n}=R \overline{T}-p \overline{V}$$

$\sum_{n} T_{i}=7009.2~К, \overline{T}=333.771~К$

$\sum_{n} V_{i}=0.0189~м^3, \overline{V}=0.0009~м^3$

$a_1=974~Па\cdot м^3$

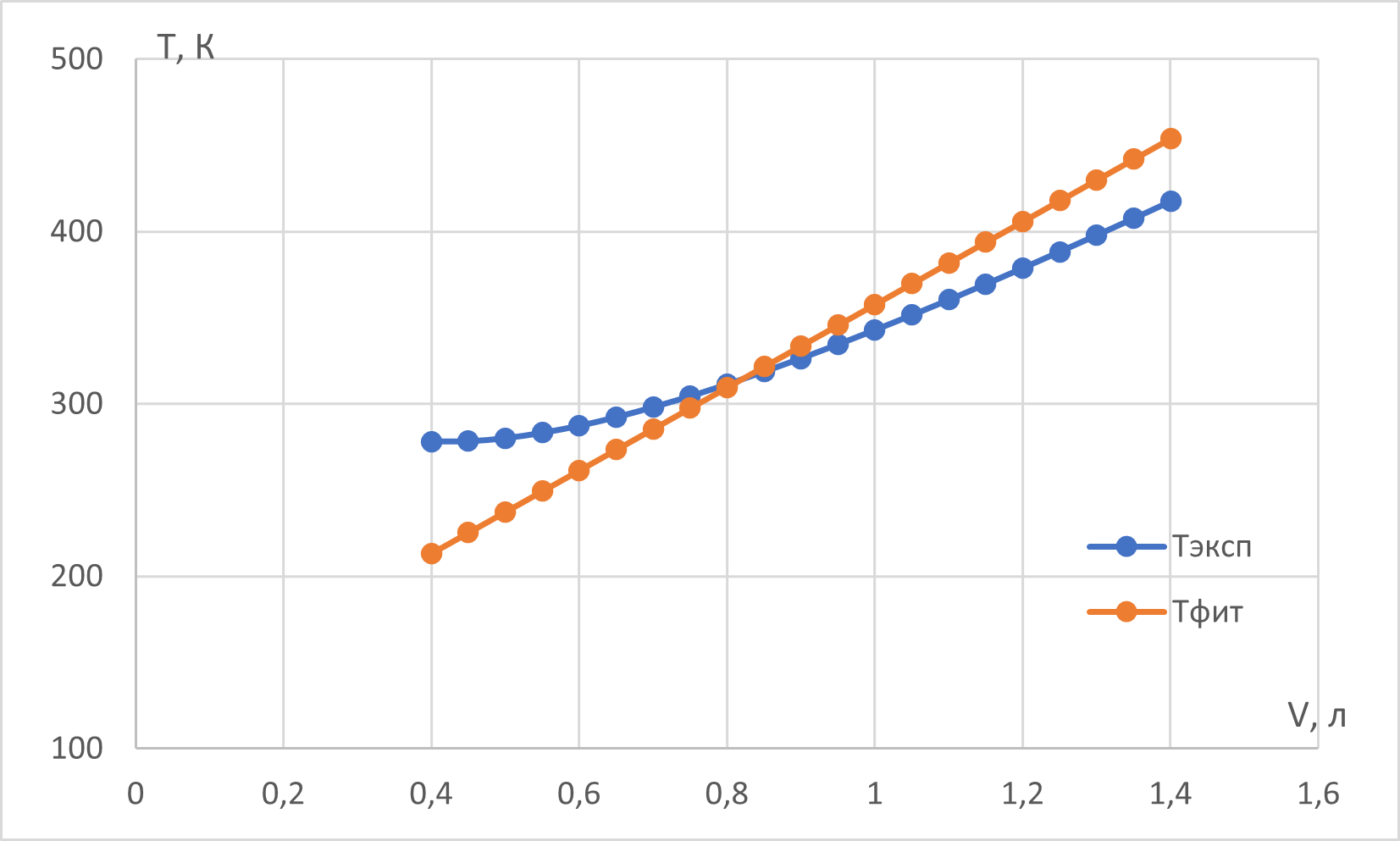
Действуем опять же формально:
$$T=\frac{p V}{R}+\frac{a_{2}}{V R}$$
$$S=\sum_{n}\left(T_{i}-\frac{p V_{i}}{R}-\frac{a_{2}}{V_{i} R}\right)^{2}$$
$$\frac{\partial S}{\partial a_{2}}=\sum_{n} 2\left(T_{i}-\frac{p V_{i}}{R}-\frac{a_{2}}{V_{i} R}\right)\left(-\frac{1}{V_{i} R}\right)=0$$
$$-\frac{1}{R} \sum_{n} \frac{T_{i}}{V_{i}}+\frac{p}{R^{2}} \sum_{n} 1+\frac{a_{2}}{R^{2}} \sum_{n} \frac{1}{V_{i}^{2}}=0$$
Откуда окончательно получаем:
$$a_{2}=\frac{R \sum_{n} \frac{T_{i}}{V_{i}}-p n}{\sum_{n} \frac{1}{V_{i}^{2}}}=\frac{R\overline{\left(\frac{T}{V}\right)}-p}{\overline{\left(\frac{1}{V^{2}}\right)}}$$

$\textit{Примечание:}$ Интуитивно можно было бы пойти путем линеаризации $p V^{2}+a_{2}=R T V$, и по аналогии с пунктом B1 написать, что $a_{2}=R \overline{T V}-p \overline{V^{2}}$. Это ошибочный путь и неверное решение. При расчете таким способом оценка для $a_2$ будет "смещенной". В решении пункта C3 мы рассчитаем значения обоими способами и убедимся в том, что применение линеаризации приводит к более высокому значению суммы квадратов отклонений.

$\sum_{n} \frac{T_{i}}{V_{i}}=8489686~К/м^3, \overline{\left(\frac{T}{V}\right)}=404271~К/м^3$

$\sum_{n} \frac{1}{V_{i}^{2}}= 39221160~м^{-6}, \overline{\left(\frac{1}{V^{2}}\right)}=1867674~м^{-6}$

$a_2=0.728~Па\cdotм^6$
Для расчета $a_2^*$ для линеаризованной зависимости у нас уже посчитаны все величины (пункт А2). Поэтому $a_2^*=0.805$. Если рассчитать $S(a_2^*)=8813~К^2$, то оно окажется больше, чем $S(a_2)=5478~К^2$.

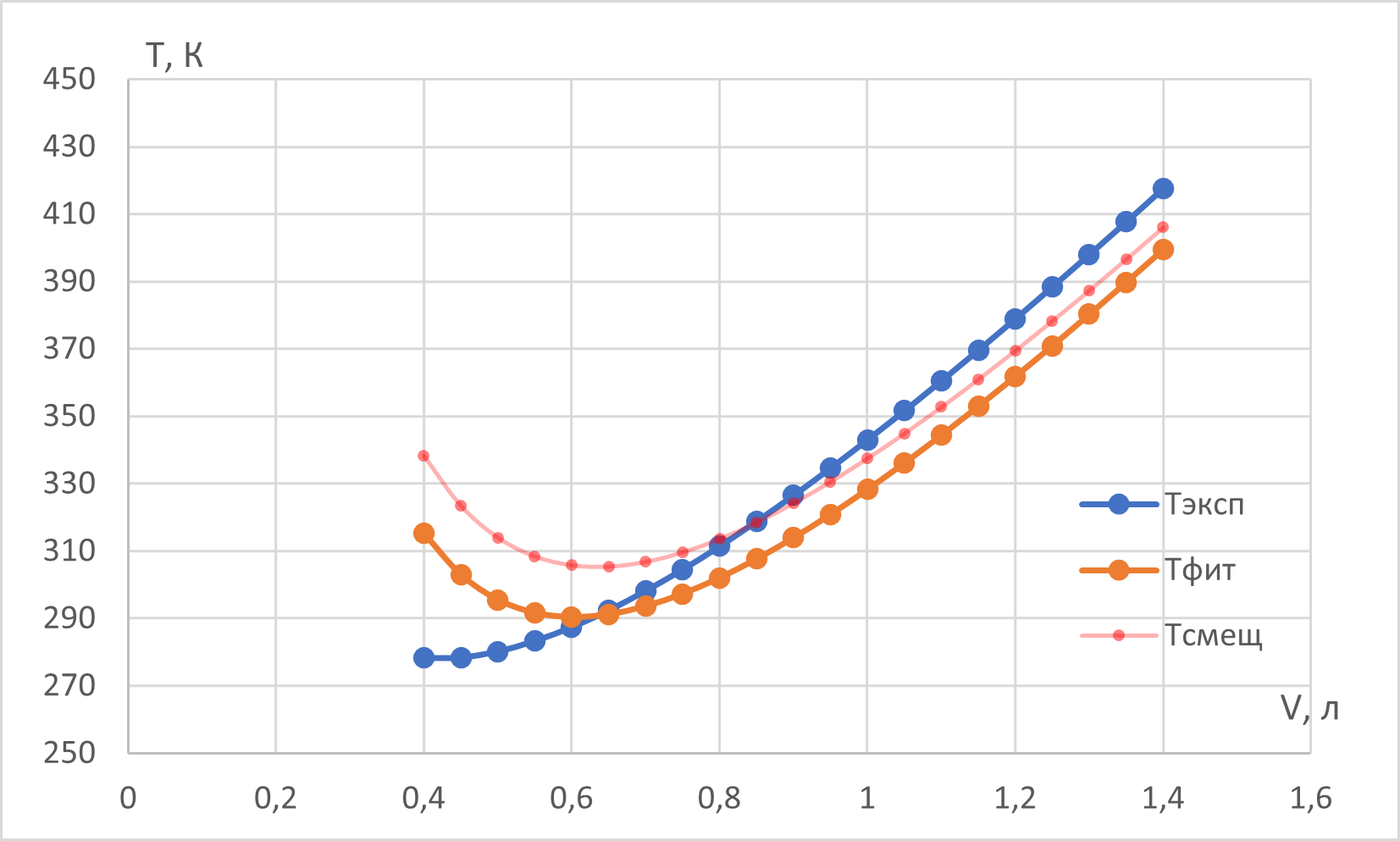
Действуем опять же формально:
$$T=\frac{p V}{R}+\frac{C}{R V}+\frac{d}{R V^{2}}$$
$$S=\sum_{n}\left(T_{i}-\frac{p V_{i}}{R}-\frac{c}{R V_{i}}-\frac{d}{R V_{i}^{2}}\right)^{2}$$
Дифференцируя, получаем систему уравнений:
$$\frac{\partial S}{\partial c}=\sum_{n} 2\left(T_{i}-\frac{p V_{i}}{R}-\frac{c}{R V_{i}}-\frac{d}{R V_{i}^{2}}\right)\left(-\frac{1}{R V_{i}}\right)=0$$
$$\frac{\partial S}{\partial d}=\sum_{n} 2\left(T_{i}-\frac{p V_{i}}{R}-\frac{C}{R V_{i}}-\frac{d}{R V_{i}^{2}}\right)\left(-\frac{1}{R V_{i}^{2}}\right)=0$$
Преобразуем систему:
$$R \sum_{n} \frac{T_{i}}{V_{i}}-p \sum_{n} 1-c \sum_{n} \frac{1}{V_{i}^{2}}-d \sum_{n} \frac{1}{V_{i}^{3}}=0$$
$$R \sum_{n} \frac{T_{i}}{V_{i}^{2}}-p \sum_{n} \frac{1}{V_{i}}-c \sum_{n} \frac{1}{V_{i}^{3}}-d \sum_{n} \frac{1}{V_{i}^{4}}=0$$
Перейдем к средним значениям и приведем систему к удобному виду:
$$c \overline{V^{-2}}+d \overline{V^{-3}}=R \overline{T / V}-p$$
$$c \overline{V^{-3}}+d \overline{V^{-4}}=R \overline{T / V^{2}}-p \overline{V^{-1}}$$
Откуда, решая совместно уравнения, получим ответы:
$$c=\frac{R\left(\overline{T / V^{2}}\,\overline{V^{-3}}-\overline{T / V}\,\overline{V^{-4}}\right)-p\left(\overline{V^{-1}}\,\overline{V^{-3}}-\overline{V^{-4}}\right)}{\left(\overline{V^{-3}}\right)^{2}-\overline{V^{-2}}\,\overline{V^{-4}}}$$
$$d=\frac{R\left(\overline{T / V^{2}}\,\overline{V^{-2}}-\overline{T / V}\,\overline{V^{-3}}\right)-p\left(\overline{V^{-1}}\,\overline{V^{-2}}-\overline{V^{-3}}\right)}{\overline{V^{-2}}\,\overline{V^{-4}}-\left(\overline{V^{-3}}\right)^{2}}$$

$\textit{Примечание:}$ Аналогично пункту C1, можно было бы привести модельную функцию к линейной зависимости: $c V+d=R T V^{2}-p V^{3}$, и определять коэффициенты $c$ и $d$ по формулам, приведенным во введении к задаче. Это ошибочный путь и неверное решение. При расчете таким способом оценки для $c$ и $d$ будут "смещенными".

Две величины $\overline{T / V}$ и $\overline{V^{-2}}$ у нас посчитаны в пункте C2.
$\overline{V^{-1}}=1270.76~м^{-3}$

$\overline{V^{-3}}=3.13694\cdot 10^9~м^{-9}$

$\overline{V^{-4}}=5.85765\cdot 10^{12}~м^{-12}$

$\overline{T / V^2}=0.568387\cdot 10^9~К/м^6$

$c=1.02~Па\cdotм^6$

$d=-1.73\cdot10^{-4}~Па\cdotм^9$

Смещенные значения:
$c^*=1.08~Па\cdotм^6, d^*=-2.17\cdot10^{-4}~Па\cdotм^9$

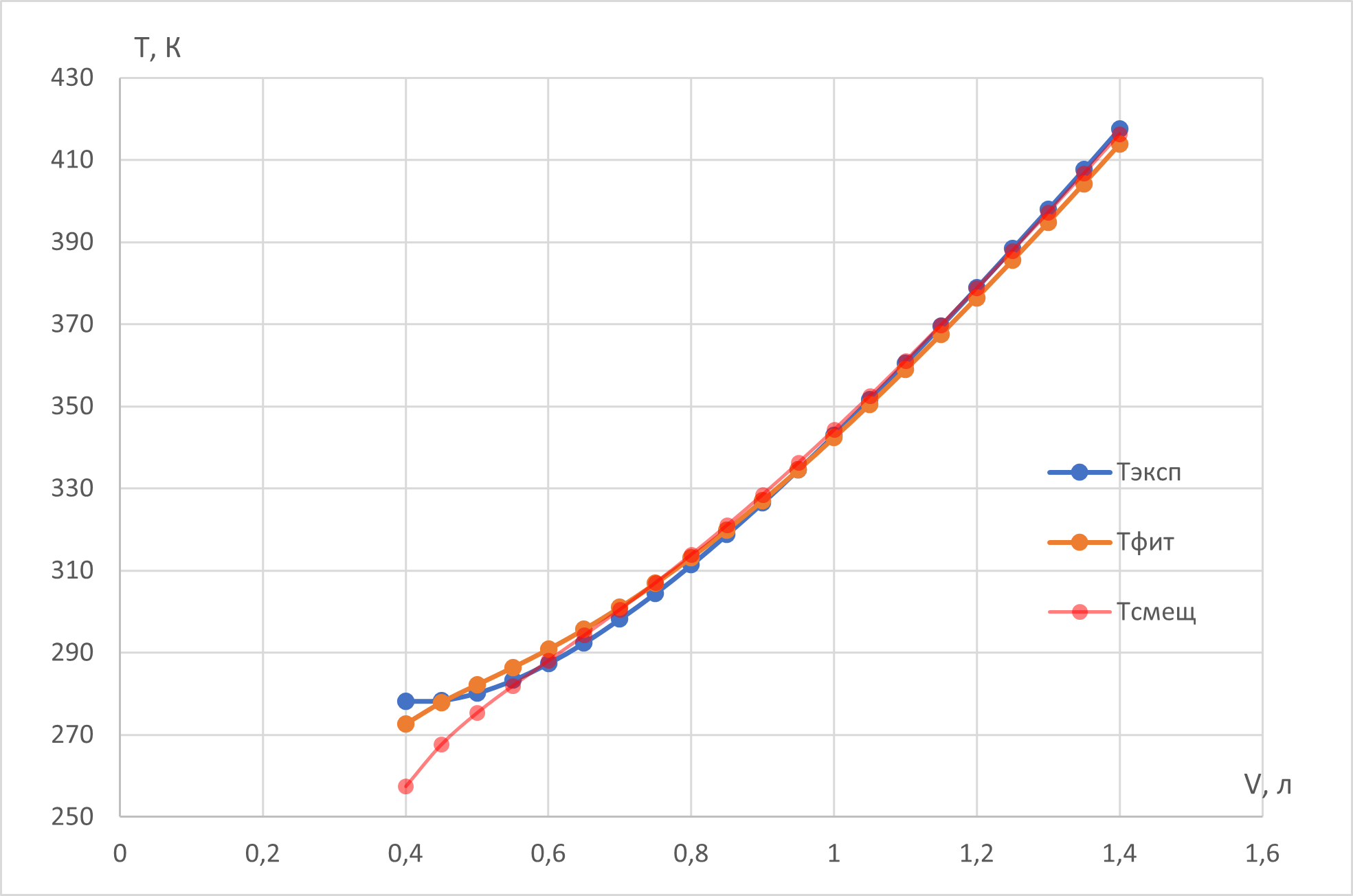
В этой части задачи нужно аналогично формально выполнить минимизацию суммы по параметрам $a$ и $b$. Итоговая система уравнений на параметры будет выглядеть следующим образом:
\begin{cases}
\alpha_1 a + \alpha_2 b + \alpha_3 ab + \alpha_4 a^2 + \alpha_5 a^2b = c_1\\
\beta_1 a + \beta_2 b + \beta_3 ab + \beta_4 b^2 + \beta_5 ab^2 = c_2
\end{cases}
Коэффициенты $\alpha_i$ и $\beta_i$ связаны целиком со средними величинами, посчитанными в пункте D2. Т.е. дополнительно ничего считать не требовалось бы.
Каждое из уравнений линейно по одной из переменной и квадратично по второй. Поэтому систему можно свести к уравнению пятой степени на одну из переменных. Уравнение пятой степени точно имеет как минимум одно действительное решение.