i  ^1.00 Если уронить одну стеклянную пластину на другую, то может быть так, что она не разобьется, а мягко остановится. На рисунке изображен этот случай: первая пластина («1» на рисунке) лежит на столе, вторая пластина («2») падает и, упираясь в небольшой выступ («3»), не скользит. Падающая пластина в начальный момент находилась в положении $A$, а в данный момент находится в положении $B$~— на небольшом расстоянии $h=h_0$ от покоящейся пластины. Угловая скорость падения пластины в данный момент равна $\omega_0$. Чему равна скорость воздуха между пластинами возле их левых ребер?

ii  ^2.50 У стеклянной пластины известны следующие параметры: ширина $L\gg h_0$, толщина $t\ll L$, плотность $\rho_g$. Длина стеклянной пластины (размер в глубину рисунка) много больше $L$. Как будет зависеть от $h$ угловая скорость пластины при ее дальнейшем движении? Плотность воздуха равна $\rho_a$. Силой тяжести, вязкостью и сжимаемостью воздуха можно пренебречь. Также считайте, что поток воздуха везде ламинарный.

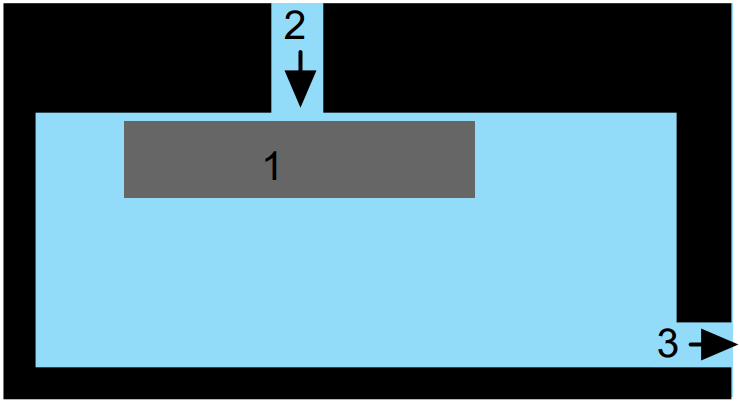
iii  ^3.00 Цилиндрический каменный диск («1» на рисунке) радиуса $R$, высоты $h$ и плотности $\rho_s$ удерживается у крышки резервуара с водой (плотность воды $\rho_w$). Из-за неровностей поверхности крышки между диском и крышкой остается небольшой зазор шириной $t\ll R$. В крышке сделано круглое отверстие («2») радиуса $r\ll R$, диск и отверстие расположили соосно (см. рис). Радиус отверстия много больше ширины зазора, $r \gg t$. В резервуар через отверстие («2») заливают воду, вытекает вода через отверстие («3»), которое находится далеко. Каким должен быть массовый расход $\mu$~(кг/с) втекающей жидкости, чтобы диск не падал? Ускорение свободного падения $g$.

iv  ^0.50 Паровые турбины широко используются в электрогенерации. Рассмотрим упрощенную модель: вода кипит при температуре $t_t=180~^\circ\mathrm C$ и давлении $p_t=10^6~Па$ (в реальности давления могут быть намного больше), а затем получившийся пар вылетает через цилиндрический канал сечением $A=1~см^2$. Давление в окружающем пространстве $p_0=10^5~Па$. Найдите измерение энтропии $\Delta S$ одного моля пара и одного моля жидкости в вылетающей струе. Молярная масса воды $M=18~г/моль$, удельная теплота парообразования при $100~^\circ\mathrm C$: $L=2.3~МДж/кг$.

v  ^3.00 Найдите массовый расход $\mu$ получившейся струи. Найдите также долю $r$ воды, находящейся в струе в жидкой фазе. Считайте, что при движении к каналу и в канале, расширение паров воды обратимо (т.е. теплопроводностью можно пренебречь, и жидкая и газообразная фаза всегда находятся в равновесии). Показатель адиабаты водяного пара $\gamma = 4/3$.