
| A1. 2 $X_{sample} \in [3400; 4000]~\text{мкм}$ | 0.15 |
|
| A1. 3 $X_{sample} \in [3100; 4300]~\text{мкм}$ | 0.10 |
|
| A1. 4 $Y_{sample} \in [-3400; -2400]~\text{мкм}$ | 0.15 |
|
| A1. 5 $Y_{sample} \in [-3900; -1900]~\text{мкм}$ | 0.10 |
|
|
A2. 1
Изображена интерференционная картина

|
0.10 |
|
| A2. 2 Для первого порядка: $$S_{-1} \in [0.30; 0.46]~\text{см}$$ $$S_{+1} \in [0.26; 0.42]~\text{см}$$ | 0.15 |
|
| A2. 3 Для второго порядка: $S_{\pm 1} \in [0.90; 1.06]~\text{см}$ | 0.15 |
|
| A2. 4 $\Delta S \in [0.61; 0.69]~\text{см}$ | 0.10 |
|
| B1. 1 $d=\frac{m \lambda}{\sin \left(\mathrm{arctg}\left(\frac{S}{L}\right)\right)}$ (засчитывать независимо от наличия коэффициента 1.22 и независимо от приближения малых углов) | 0.50 |
|
| B2. 1 Заполнены строки $(x, y)$ и $S$ для трех видимых лазеров | 3 × 0.25 |
|
|
B2. 2
Узкие ворота:
$\mathrm{arctg}\left(\frac{\overline{S_{488}}}{L}\right) \in [0.0899; 0.1099]$ $\mathrm{arctg}\left(\frac{\overline{S_{514}}}{L}\right) \in [0.0951; 0.1163]$ $\mathrm{arctg}\left(\frac{\overline{S_{633}}}{L}\right) \in [0.1165; 0.1423]$ $\mathrm{arctg}\left(\frac{\overline{S_{694}}}{L}\right) \in [0.1300; 0.1588]$ |
3 × 0.15 |
|
|
B2. 3
Широкие ворота:
$\mathrm{arctg}\left(\frac{\overline{S_{488}}}{L}\right) \in [0.0799; 0.1199]$ $\mathrm{arctg}\left(\frac{\overline{S_{514}}}{L}\right) \in [0.0846; 0.1268]$ $\mathrm{arctg}\left(\frac{\overline{S_{633}}}{L}\right) \in [0.1035; 0.1553]$ $\mathrm{arctg}\left(\frac{\overline{S_{694}}}{L}\right) \in [0.1155; 0.1733]$ |
3 × 0.10 |
|
B3. 1
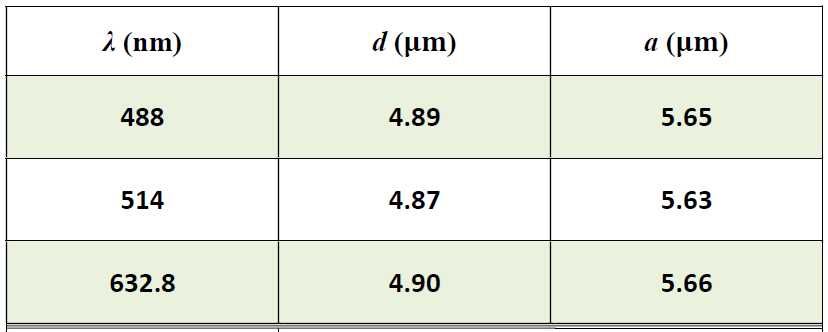
|
None |
|
| B3. 2 Верный расчет $d$ | 3 × 0.10 |
|
| B3. 3 Верный расчет $a$ | 3 × 0.20 |
|
| B3. 4 $\overline{a} \in [5.607; 5.647]~\mu m$ | 0.10 |
|
C1. 1
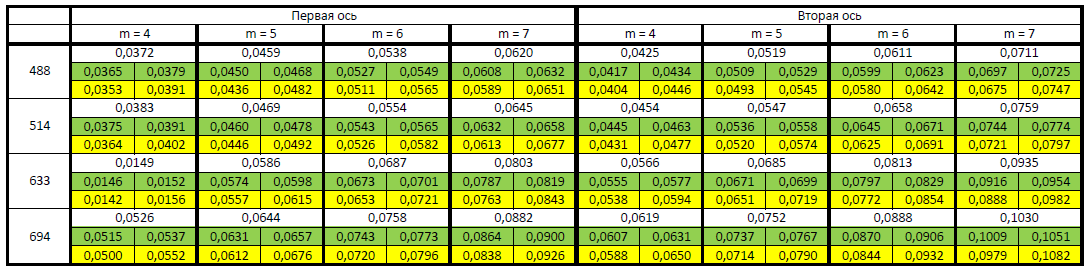
|
None |
|
| C1. 2 Первая ось: $\mathrm{arctg}\left(\frac{S}{L}\right)$ попадает в узкие ворота (см. зеленые строки) для четырех порядков для выбранного лазера | 4 × 0.05 |
|
| C1. 3 Первая ось: $\mathrm{arctg}\left(\frac{S}{L}\right)$ попадает в широкие ворота (см. желтые строки) для четырех порядков для выбранного лазера | 4 × 0.05 |
|
| C1. 4 Вторая ось: $\mathrm{arctg}\left(\frac{S}{L}\right)$ попадает в узкие ворота (см. зеленые строки) для четырех порядков для выбранного лазера | 4 × 0.05 |
|
| C1. 5 Вторая ось: $\mathrm{arctg}\left(\frac{S}{L}\right)$ попадает в широкие ворота (см. желтые строки) для четырех порядков для выбранного лазера | 4 × 0.05 |
|
C2. 1
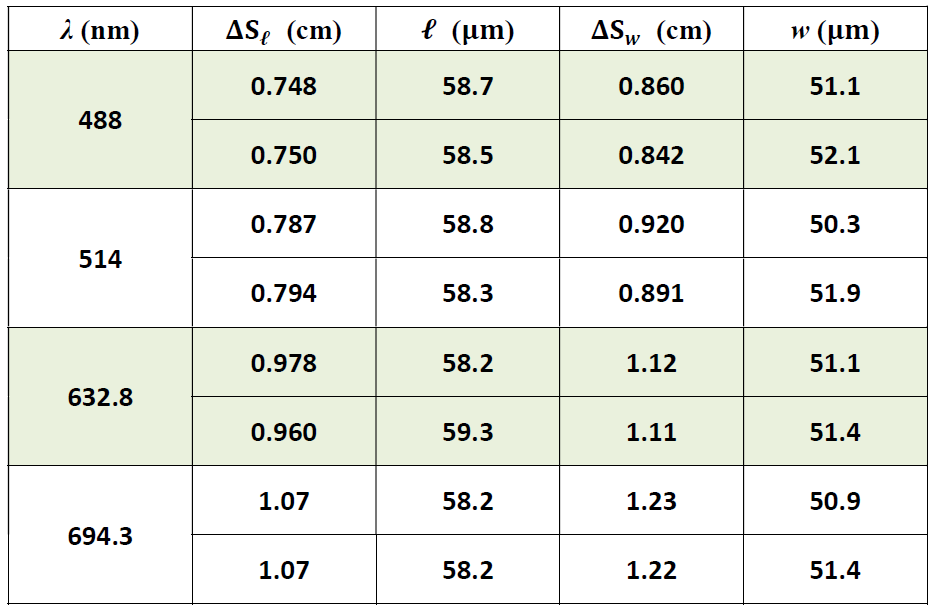
|
None |
|
| C2. 2 Верный расчет $\Delta S_l$ | 0.10 |
|
| C2. 3 В расчете $\Delta S_l$ использовано усреднение | 0.05 |
|
| C2. 4 Верный расчет $\Delta S_w$ | 0.10 |
|
| C2. 5 В расчете $\Delta S_w$ использовано усреднение | 0.05 |
|
| C2. 6 Верный расчет $l$ | 0.20 |
|
| C2. 7 Верный расчет $w$ | 0.20 |
|
| C3. 1 Рисунок, проведена прямая | 0.40 |
|
| C3. 2 M1 $\phi$ попадает в узкие ворота: $\phi \in [25.5; 28.5]^\circ$ | 0.30 |
|
| C3. 3 M1 $\phi$ попадает в широкие ворота: $\phi \in [24; 30]^\circ$ | 0.30 |
|
| C3. 4 M2 Выбран угол $(90^\circ - \phi)$ и он попадает в узкие ворота: $(90^\circ - \phi) \in [61.5; 64.5]^\circ$ | 0.10 |
|
| C3. 5 M2 Выбран угол $(90^\circ - \phi)$ и он попадает в широкие ворота: $(90^\circ - \phi) \in [60; 66]^\circ$ | 0.10 |
|
| D1. 1 Зарисована решетка 4х4 (или хотя бы 2х2) и отмечены координаты максимумов | 1.20 |
|
| D1. 2 На рисунке отмечены отрезки $\Delta S_x$ и $\Delta S_y$ | 0.20 |
|
| D1. 3 Начат расчет величин $\Delta S_x$ и $\Delta S_y$ | 0.10 |
|
| D1. 4 Вычислены $\Delta S_x$ и $\Delta S_y$ | 0.40 |
|
D2. 1
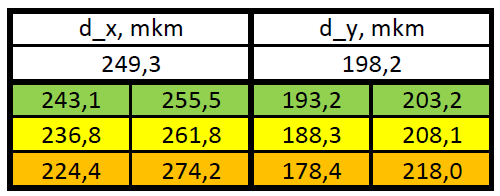
|
None |
|
| D2. 2 $d_x$ и $d_y$ попадают в узкие ворота (см. зеленые строки) | 2 × 0.10 |
|
| D2. 3 $d_x$ и $d_y$ попадают в средние ворота (см. желтые строки) | 2 × 0.10 |
|
| D2. 4 $d_x$ и $d_y$ попадают в широкие ворота (см. оранжевые строки) | 2 × 0.10 |
|
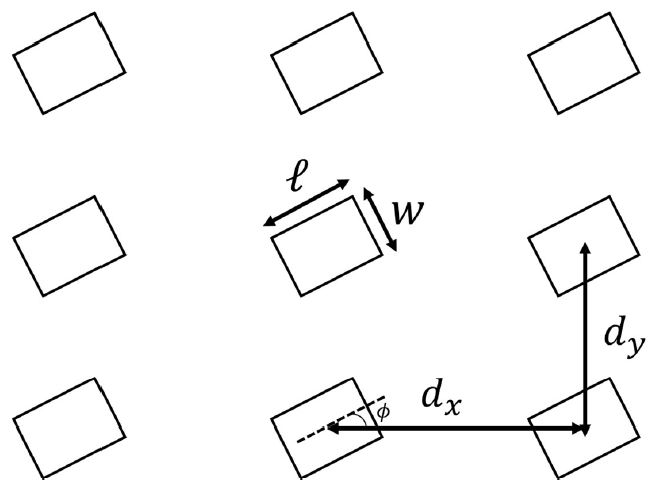
E1. 1
|
None |
|
| E1. 2 $l$ верно отмечено на рисунке | 0.20 |
|
| E1. 3 $w$ верно отмечено на рисунке | 0.20 |
|
| E1. 4 $d_x$ верно отмечено на рисунке | 0.20 |
|
| E1. 5 $d_y$ верно отмечено на рисунке | 0.20 |
|
| E1. 6 $\phi$ верно отмечено на рисунке | 0.20 |
|