
Решение в СО дороги:
Для того чтобы выполнялось условие минимальности времени, Настя:
а) должна двигаться прямолинейно, т.к. в противном случае, у нее появилась бы возможность за то же время оказаться на дороге ближе к остановке, чем при криволинейном движении
б) не должна ждать автобуса на дороге,
следовательно, девочка и автобус достигают точки встречи одновременно.
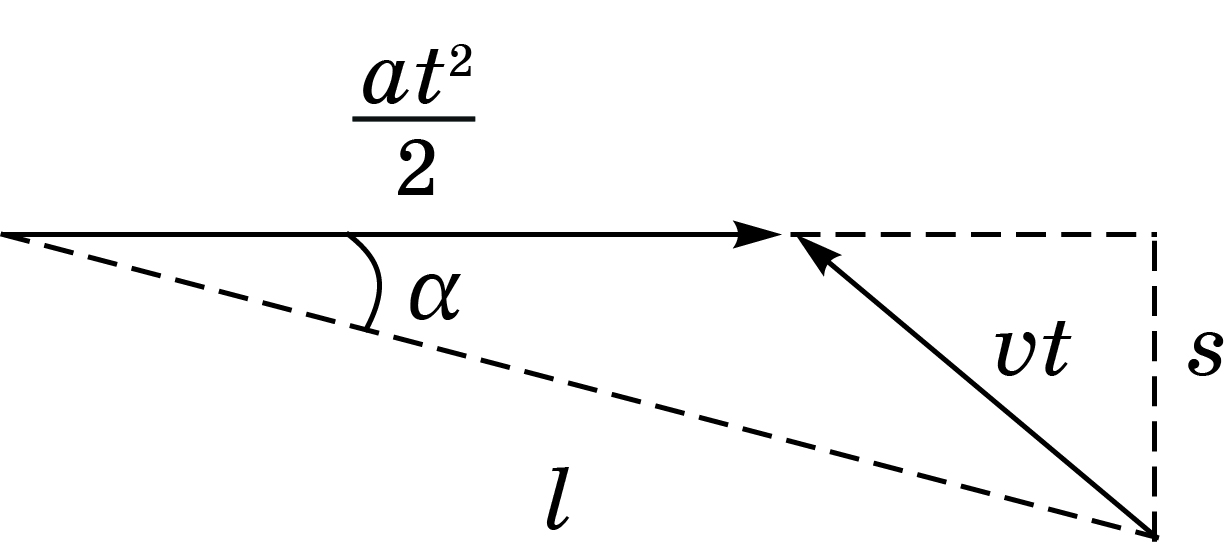
Рассмотрим прямоугольный треугольник с гипотенузой $l$: $\cos \alpha = \dfrac{\sqrt{l^2-s^2}}{l}$ (см.~рисунок). Запишем теорему косинусов:
\[ v^2t^2 = l^2 - lat^2\cos \alpha + \dfrac{a^2t^4}{4}\]
Подставив косинус в уравнение получим:
\[ v^2t^2 = l^2 - at^2\sqrt{l^2-s^2}+a^2t^4/4\]
Решение в СО автобуса:
В системе отсчета автобуса точка из которой начала движение девочка за время $t$ смещается параллельно дороге на расстояние $at^2/2$. За это время Настя может удалиться от этой точки на расстояние $vt$. Покажем эти перемещения на рисунке. Геометрическое место точек, в которых может оказаться девочка, имеет вид окружности. Минимальное время $t = \tau$ соответствует касанию окружности автобуса.
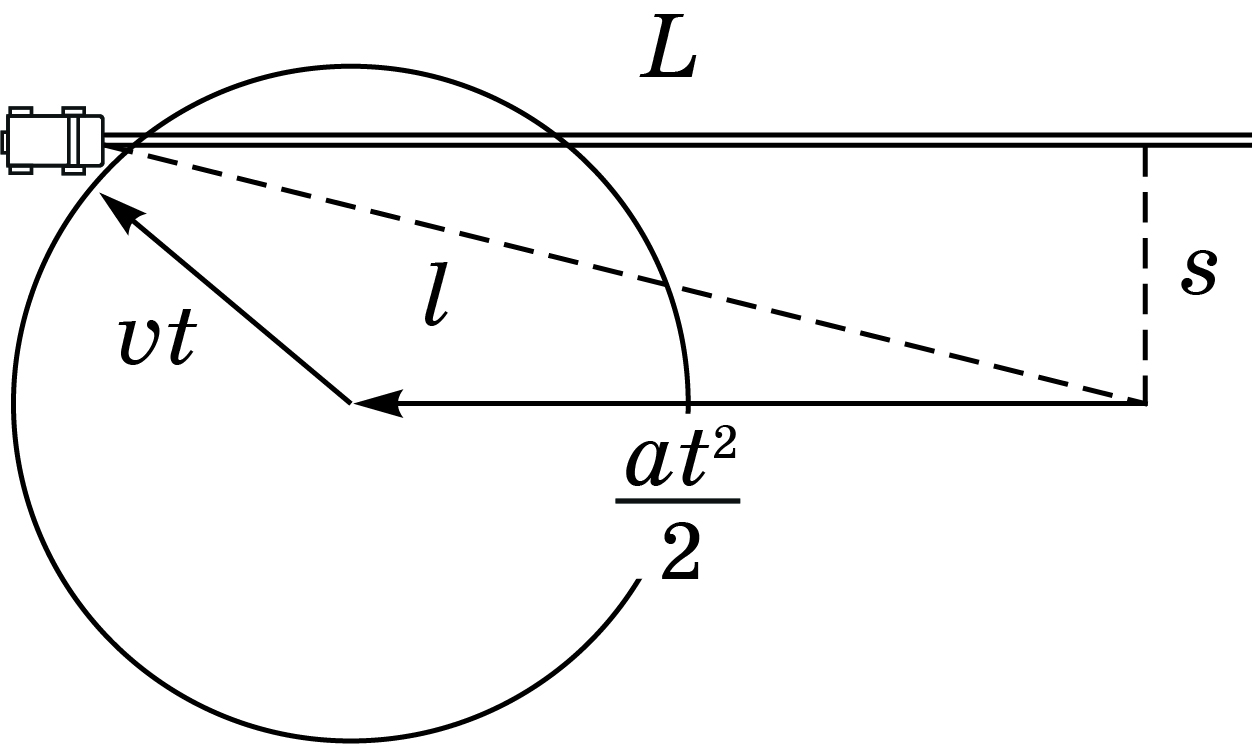
Обозначим начальное расстояние вдоль дороги между автобусом и Настей за $L$. Дважды запишем теорему Пифагора: $ L^2 = l^2 - s^2 $ и $(v\tau)^2 = (L - a\tau^2/2)^2+s^2$.
«Баллистическое» решение
Можно воспользоваться методом аналогий. Равноускоренное движение девочки в системе отсчета автобуса эквивалентно движению тела, брошенного со скоростью $v$ в поле однородной гравитации с ускорением свободного падения $a$. См. рисунок.
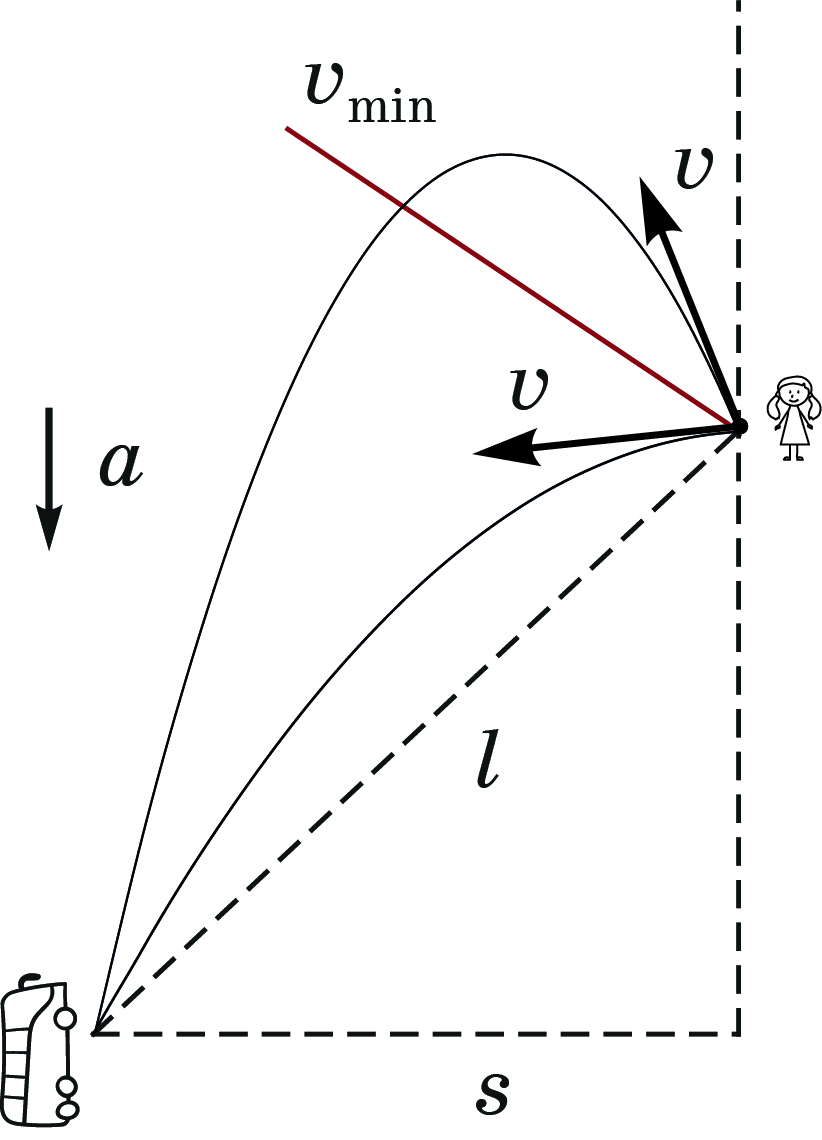
Тогда задача сводится к поиску времен движения тела с заданными начальной скоростью и ускорением в точку, находящуюся на расстоянии $s$ по горизонтали и $\sqrt{l^2-s^2}$ по вертикали.
Минимальное время достигается при движении по «настильной» траектории.
При таком подходе интуитивно понятным становится ОДЗ — не при любой начальной скорости тело сможет долететь до заданной точки.
Решая биквадратное уравнение относительно времени, получим:
\[ \tau = \sqrt{\dfrac{4(aL+v^2)\pm \sqrt{4^2(aL+v^2)^2-16a^2l^2}}{2a^2}}\]
Видно, что подкоренное выражение всегда положительное, т.к. $4(aL+v^2) > \sqrt{4^2(aL+v^2)^2-16a^2l^2}$.
Выбираем меньший из двух корней из соображений минимальности времени. Чтобы решение существовало, выражение под внутренним корнем должно быть положительным: $v^4+2v^2 La-a^2s^2>0$, иначе Настя не успеет даже добежать до дороги, по которой пронесется автобус, быстро набравший большую скорость.