$\textbf{Метод №1}$
Обозначим за $m_1$ массу большего груза, а за $m_2$ — массу меньшего. В силу нерастяжимости нити модули скоростей и ускорений, с которыми движутся грузы, равны. Будем считать, что нить не проскальзывает по блоку, поэтому
\begin{equation}
v = \omega r.
\tag{1}
\end{equation}
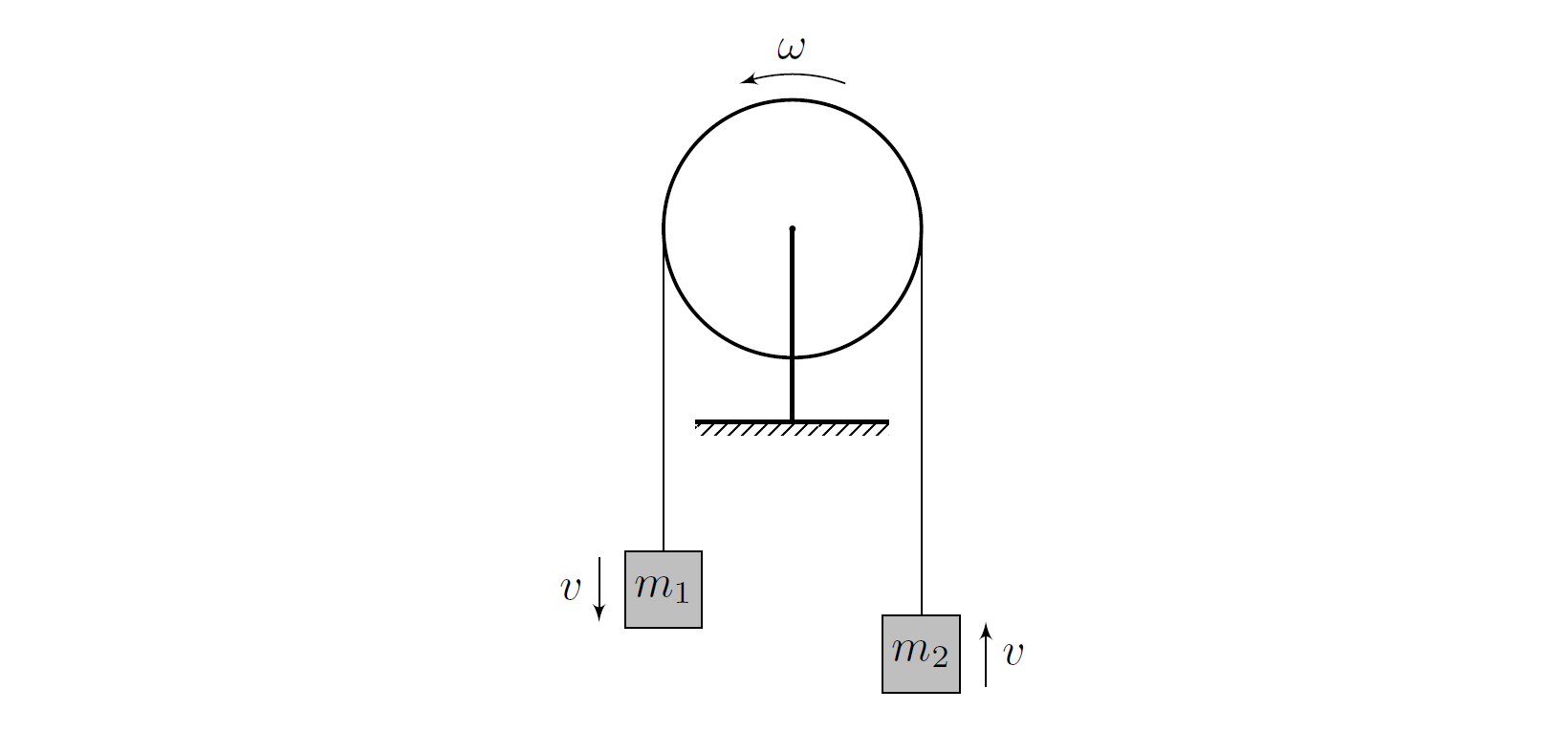
Рассмотрим систему из блока и грузов. В ней сохраняется механическая энергия, так как трением в оси блока можно пренебречь. Выберем малый промежуток времени $dt$ и, учитывая уравнение $(1)$, запишем ЗСЭ:
\[ \frac{m_1 v^2}{2} + \frac{m_2 v^2}{2} + \frac{m_\text{эфф} v^2}{2} =\\ \frac{m_1 (v + a\,dt)^2}{2} + \frac{m_2 (v + a\,dt)^2}{2} + \frac{m_\text{эфф} (v + a\,dt)^2}{2} + (m_2 - m_1) g v \, dt,\]
где $a$ — это ускорение грузов. Пренебрегая вторым порядком малости, упростив выражение, получим:
\begin{equation}
(m_1 + m_2 + m_\text{эфф}) a = (m_1 - m_2) g.
\tag{2}
\end{equation}
Проведем оценку того, при какой разнице масс $m_1$ и $m_2$ блок покоится. Например, когда $m_1=m$, $m_2=2 m_\text{с}$(с одной стороны маленькая гайка, а с другой две скрепки) — блок покоится, а когда $m_1=m+m_\text{с}$, $m_2=m$ (с одной стороны маленькая гайка, а с другой только скрепка) — блок движется. Можно сделать вывод, что блок покоится при $|m_1-m_2|<0{,}4~\text{г}$.
Теперь проведем следующий эксперимент: при разных $m_1$ и $m_2$ будем измерять время, за которое изначально покоящийся груз $m_1$ проходит расстояние $L$ от края стола до пола.
\[ L = (72{,}9 \pm 0{,}2)~\text{см}. \]
Массы $m_1$ и $m_2$ можно изменять подвешивая гайки на скрепки, а значения найти по формулам:
\[ m_1 = N_{1\text{б}} M + N_{1\text{м}} m + m_\text{с} \]\[ m_2 = N_{2\text{б}} M + m_\text{с}, \]
где $N_{1\text{б}}$ — количество больших гаек слева, $N_{1\text{м}}$ — количество маленьких гаек слева, $N_{2\text{б}}$ — количество больших гаек справа.
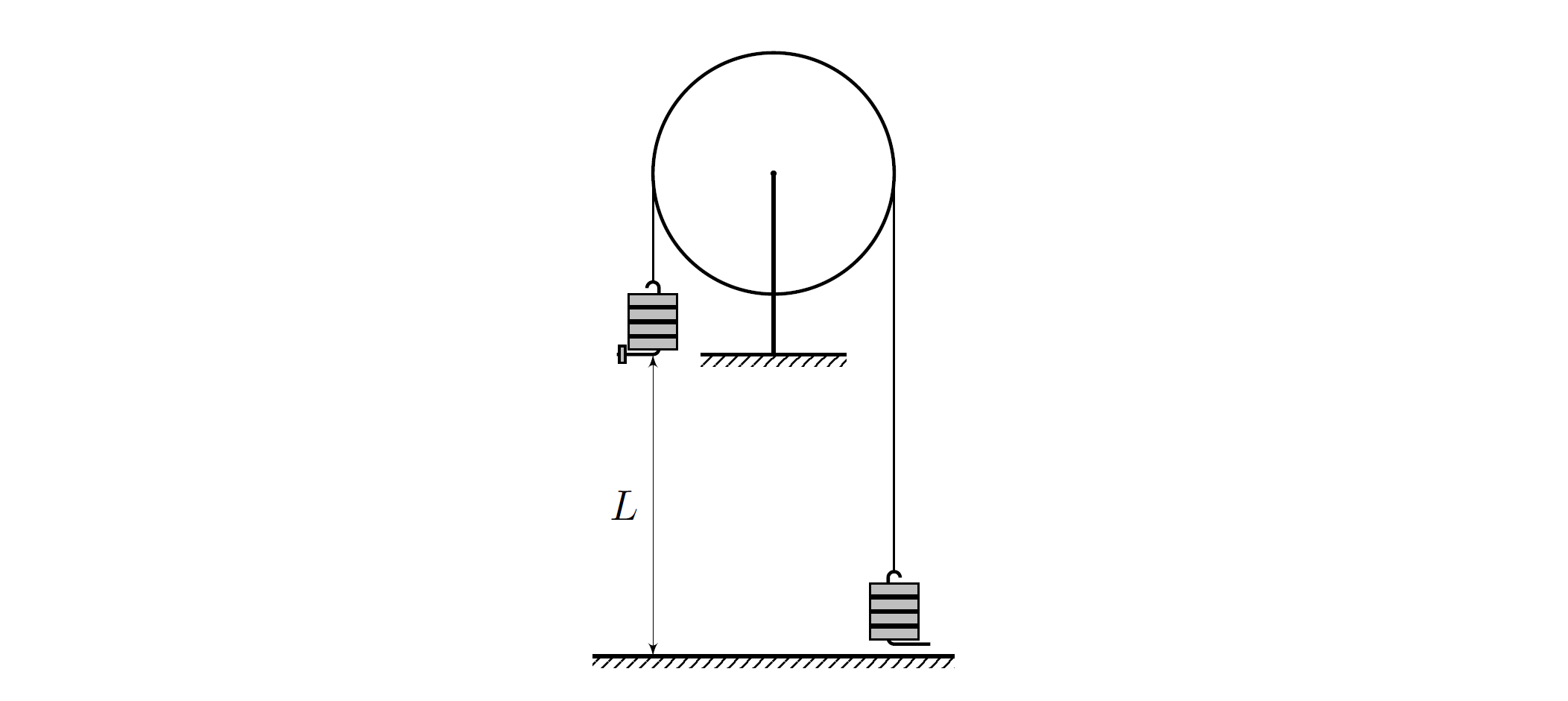
Возьмем $N_{1\text{б}}=1$, $N_{1\text{м}}=1$, $N_{2\text{б}}=1$ и три раза измерим время, за которое изначально покоящийся груз $m_1$ проходит расстояние $L$.
В силу того, что приборная погрешность измерения времени гораздо меньше случайной, в дальнейшем будем проводить по 3 измерения, а ускорение $a$ считать по формуле:
\[ a = 2\frac{L}{\langle t\rangle ^2},\]
где $\langle t \rangle$ — это среднее время, которое вычисляется следующим образом: $\langle t \rangle = \dfrac{1}{3} \left( t_1 + t_2 + t_3 \right)$.
Согласно выражению $(2)$ можно выбрать координаты $Y_1 = m_1 + m_2$, $X_1 = \dfrac{g}{a} (m_1 - m_2)$, в которых график должен оказаться линейным: $Y_1 = X_1 - m_\text{эфф}$. Формула для пересчета:
\[ X_1=\frac{g\langle t \rangle ^2}{2L} (m_1 - m_2). \]
При построении графика точки №8 и №12 мы не будем использовать, так как они имеют слишком большие погрешности в сравнении с другими точками. При этом важно отметить, что в рамках крестов ошибок эти точки лежат на нашей прямой.
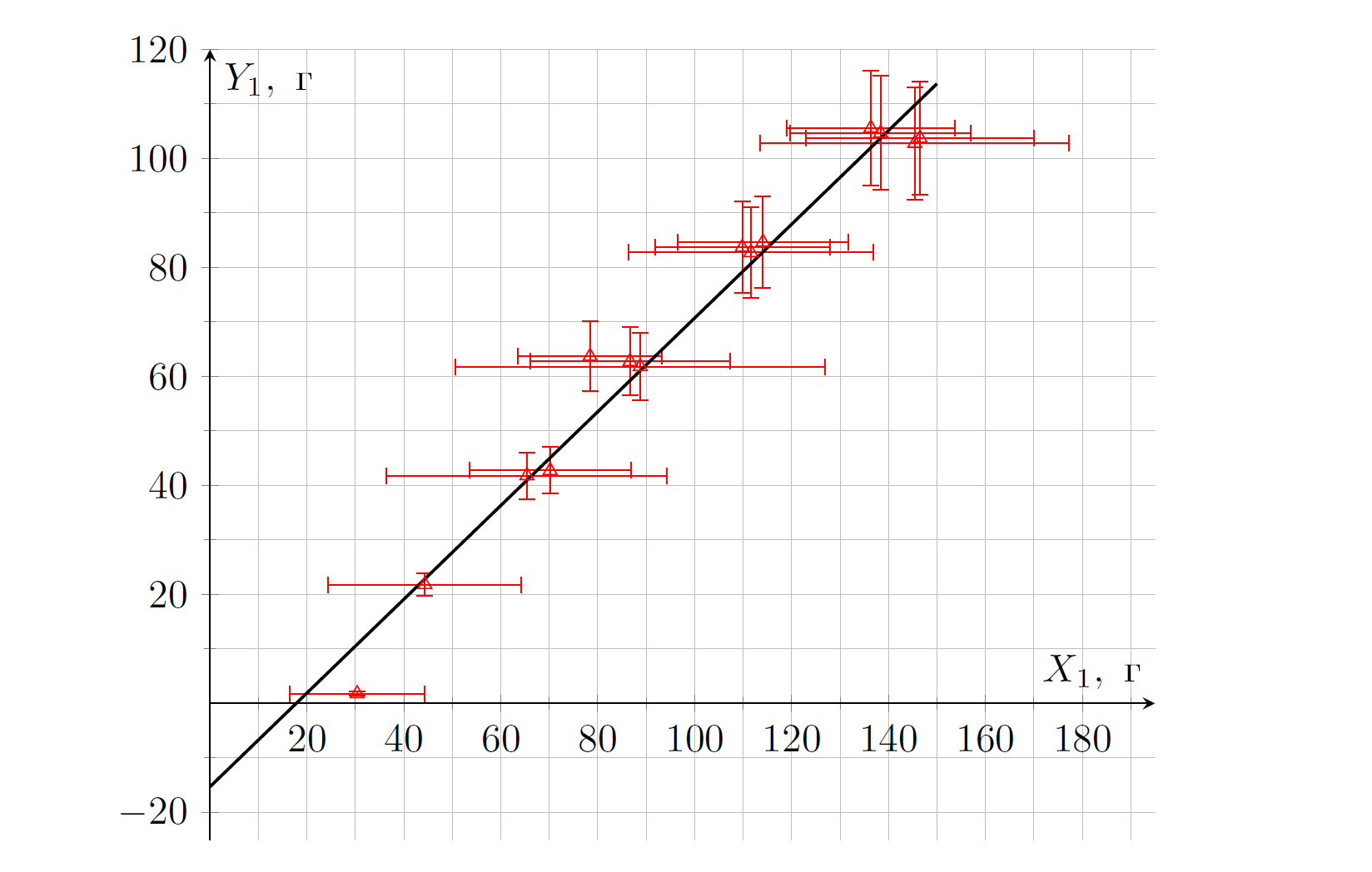
Найдем из графика $m_\text{эфф}= (15 \pm 5)~\text{г}$. Стоит отметить, что коэффициент наклона немного отличен от единицы, что можно объяснить трением в подшипнике.
$\textbf{Метод №2}$
Для определения $m_\text{эфф}$ можно использовать колебания. Чтобы превратить блок в физический маятник, мы можем с помощью клейкой массы приклеить большую гайку к краю блока. Расстояние от центра блока до гайки обозначим за $l$.
Запишем ЗСЭ, пренебрегая трением. За $\alpha$ обозначим малый угол отклонения от положения равновесия:
\begin{equation}
\frac{m_\text{эфф} \omega^2 r^2}{2} + \frac{M \omega^2 l^2}{2} + Mgl (1-\cos \alpha) = \text{const},
\tag{3}
\end{equation}
при этом $d \alpha = \omega \, dt$, $\cos \alpha \simeq 1 - \alpha^2/2$. Подставим это в выражение $(3)$:
\[ \frac{1}{2} \left( m_\text{эфф} r^2 + M l^2 \right) \omega^2 + \frac{1}{2} Mgl \, \alpha^2 = \text{const}. \]
Получилось уравнение колебаний с периодом $T$:
\[ T = 2 \pi \sqrt{ \frac{m_\text{эфф} r^2 + Ml^2}{Mgl}}.\]
Проведем измерения: $l=(4{,}5 \pm 0{,}1)~\text{см}$, $r=(4{,}9\pm0{,}1)~\text{см}$. Измерим время $t$ за, которое происходит $n=10$ колебаний. Формула для нахождения $m_\text{эфф}$:
\[ m_\text{эфф} = M \left( \frac{T^2}{4 \pi^2}\frac{gl}{r^2} - \frac{l^2}{r^2} \right).\]
По данной формуле получается следующий результат: $m_\text{эфф}=(25 \pm 6)~\text{г}$. Результат получается немного завышеным из-за трения в подшипнике.
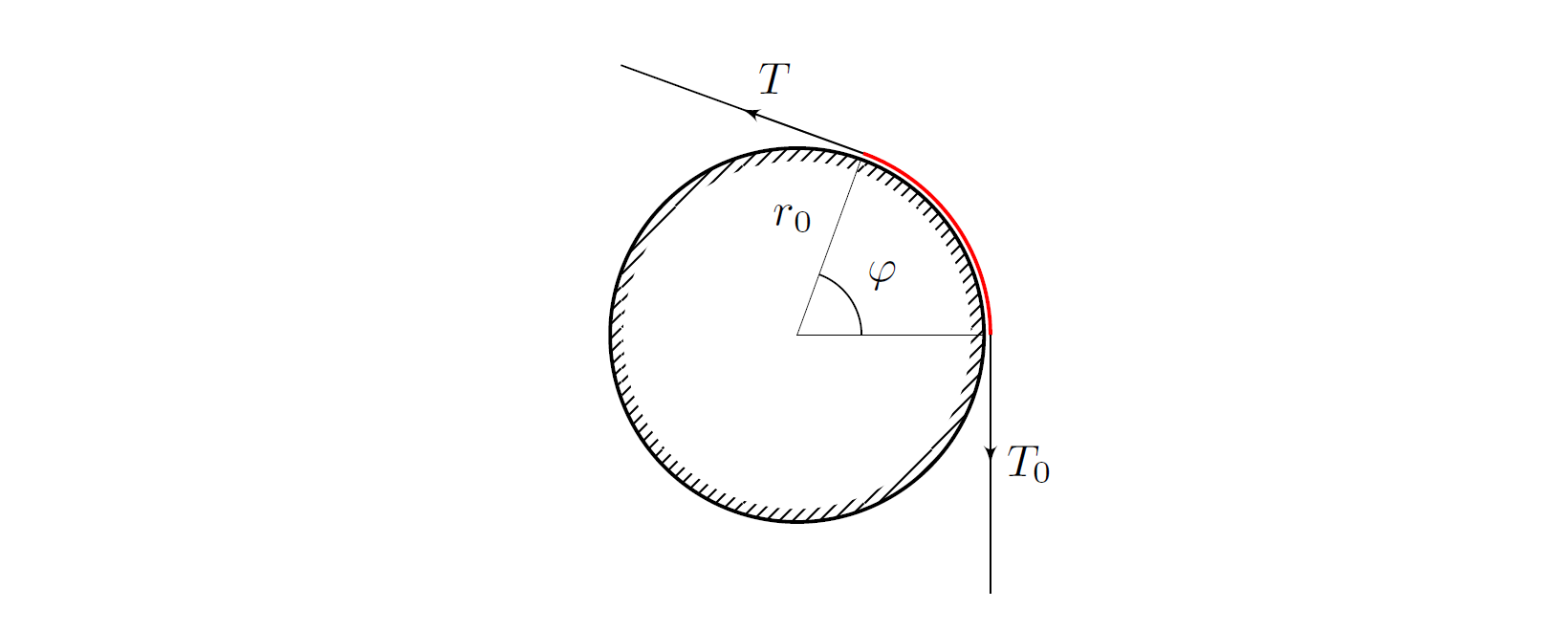
Рассмотрим нить, которая огибает карандаш радиуса $r_0$ по дуге окружности соотвествующей углу $\varphi$. Пусть сила натяжения с одной стороны равна $T_0$, а с другой $T$, причем $T_0
Запишем уравнения движения нити (нить невесома). Для этого рассмотрим малый участок нити — дугу окружности соответствующую малому углу $d \varphi$ и действующие на него силы.
\[ d N = T \, d \varphi, \]\[ \mu \, d N \, r_0 + T r_0 = (T + d T) r_0. \]
$\textbf{Динамический метод}$
За время $d t$ сила трения совершает работу $-(T-T_0) v \, d t$, поэтому из закона сохранения энергии и $(4)$ мы получаем:
Преобразуем выражение $(5)$:
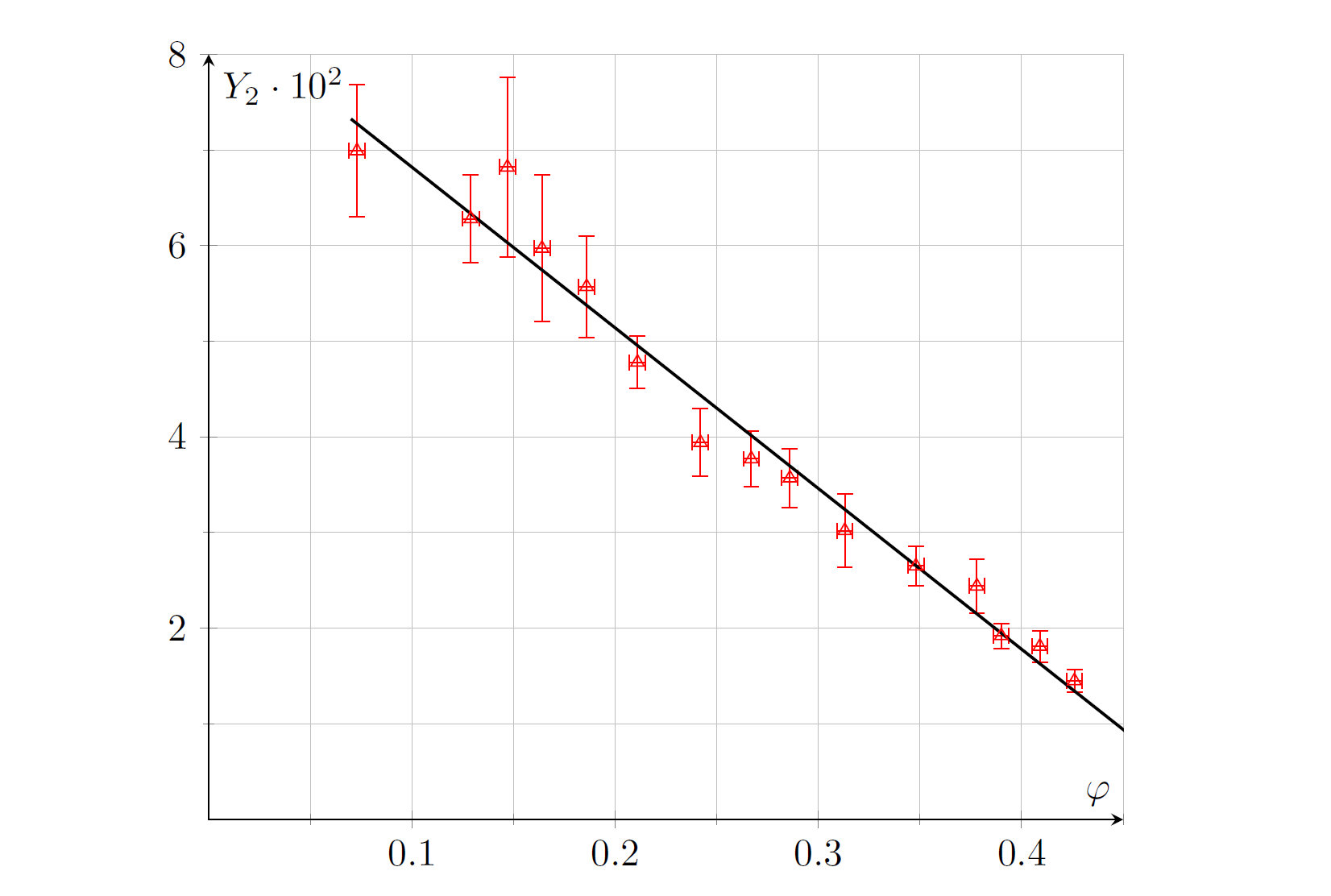
Из графика найдем угловой коэффициент $k_2 = -\mu = -(0{,}17 \pm 0{,}02)$. Значит $\mu = (0{,}17 \pm 0{,}02)$.
$\textbf{Статический метод}$
В итоге, опираясь на $(4)$, можно написать равенство:
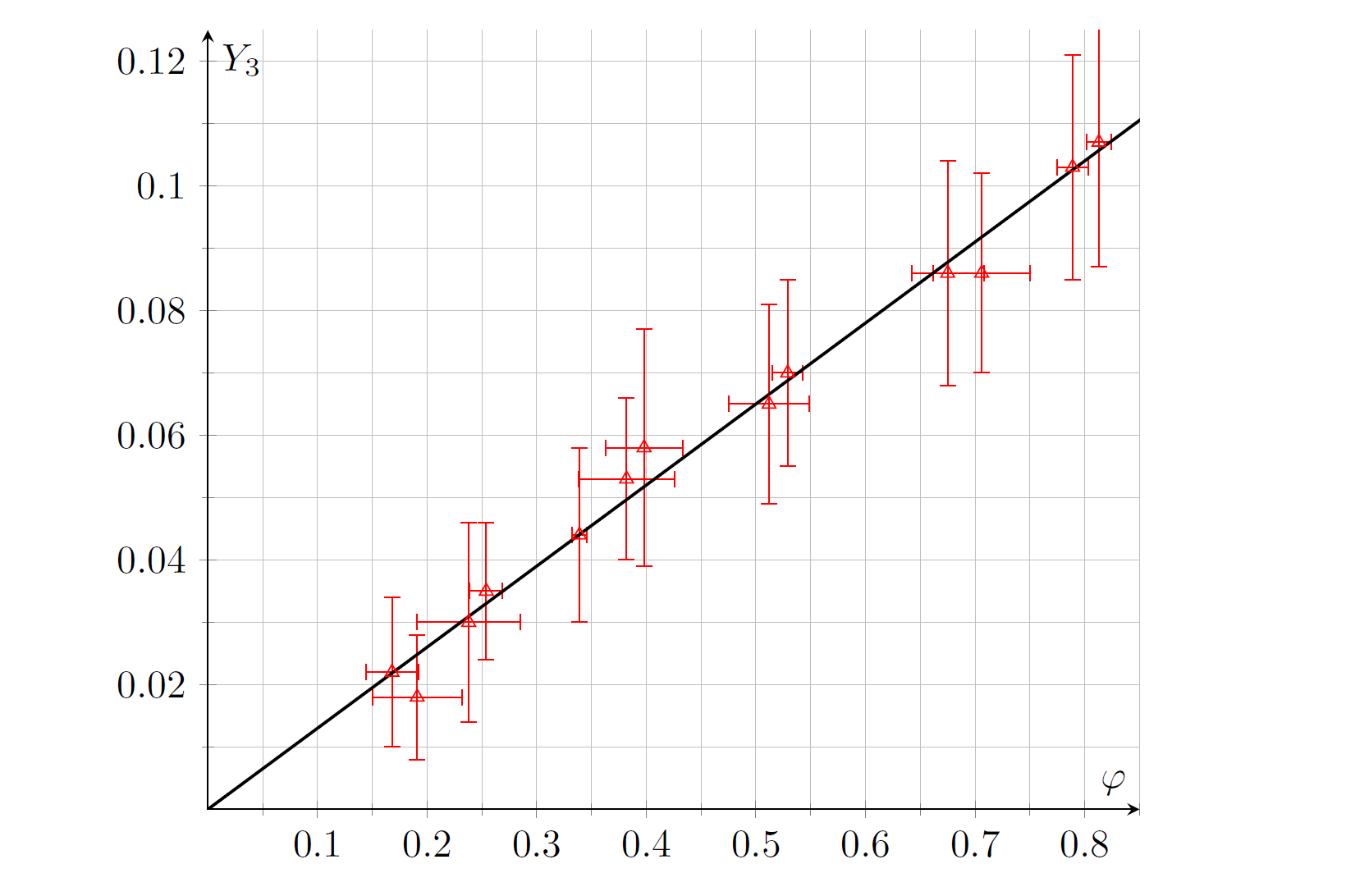
Коэффициент наклона $k_3=(0{,}13 \pm 0{,}04)$, значит $\mu=(0{,}13 \pm 0{,}04)$.
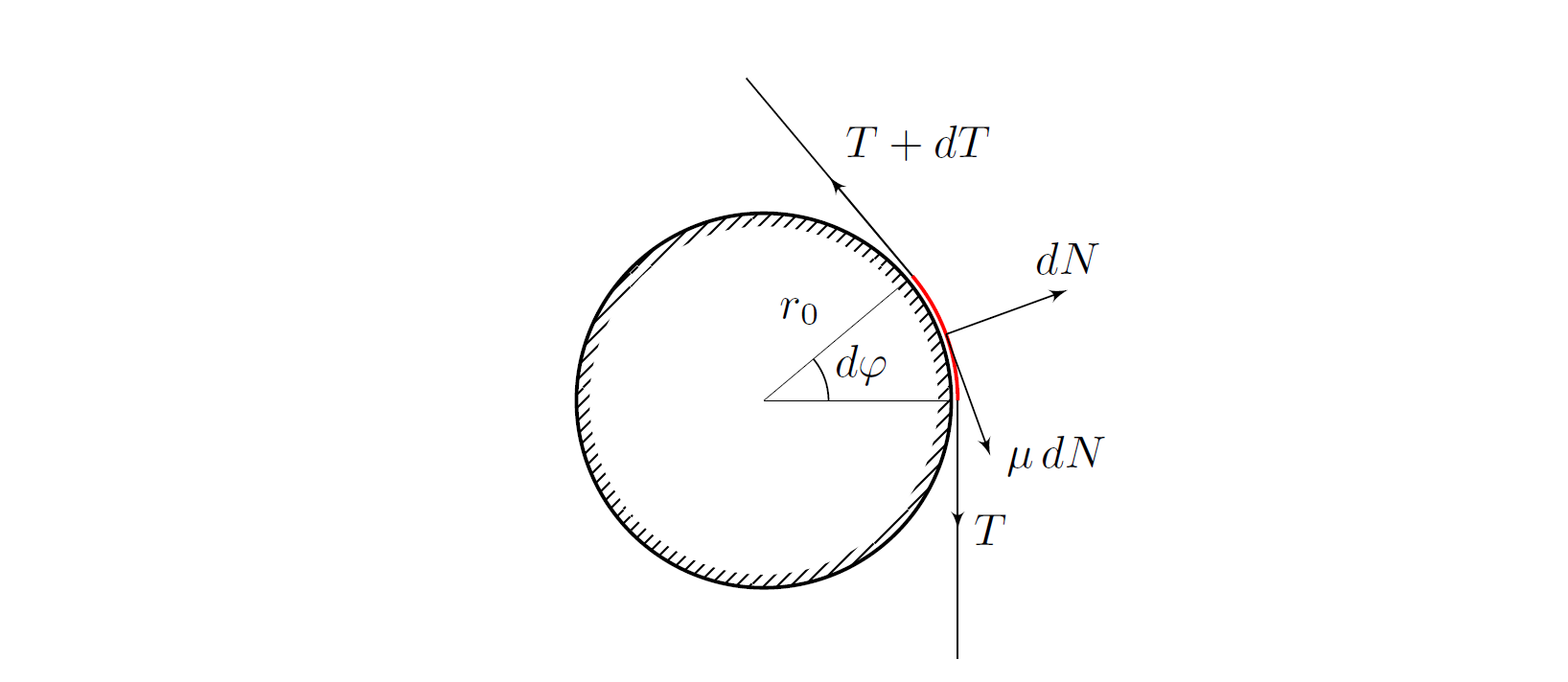
Тогда выполняется:
\[ \mu T \, d \varphi = dT,\]
а учитывая, что $T-T_0 \ll T$:
\begin{equation}
\mu \varphi = \frac{T-T_0}{T}
\tag{4}
\end{equation}
Тот же результат можно получить используя предельный переход от точной формулы Эйлера $T = T_0 e^{\mu \varphi}$ в случае $T-T_0 \ll T$.
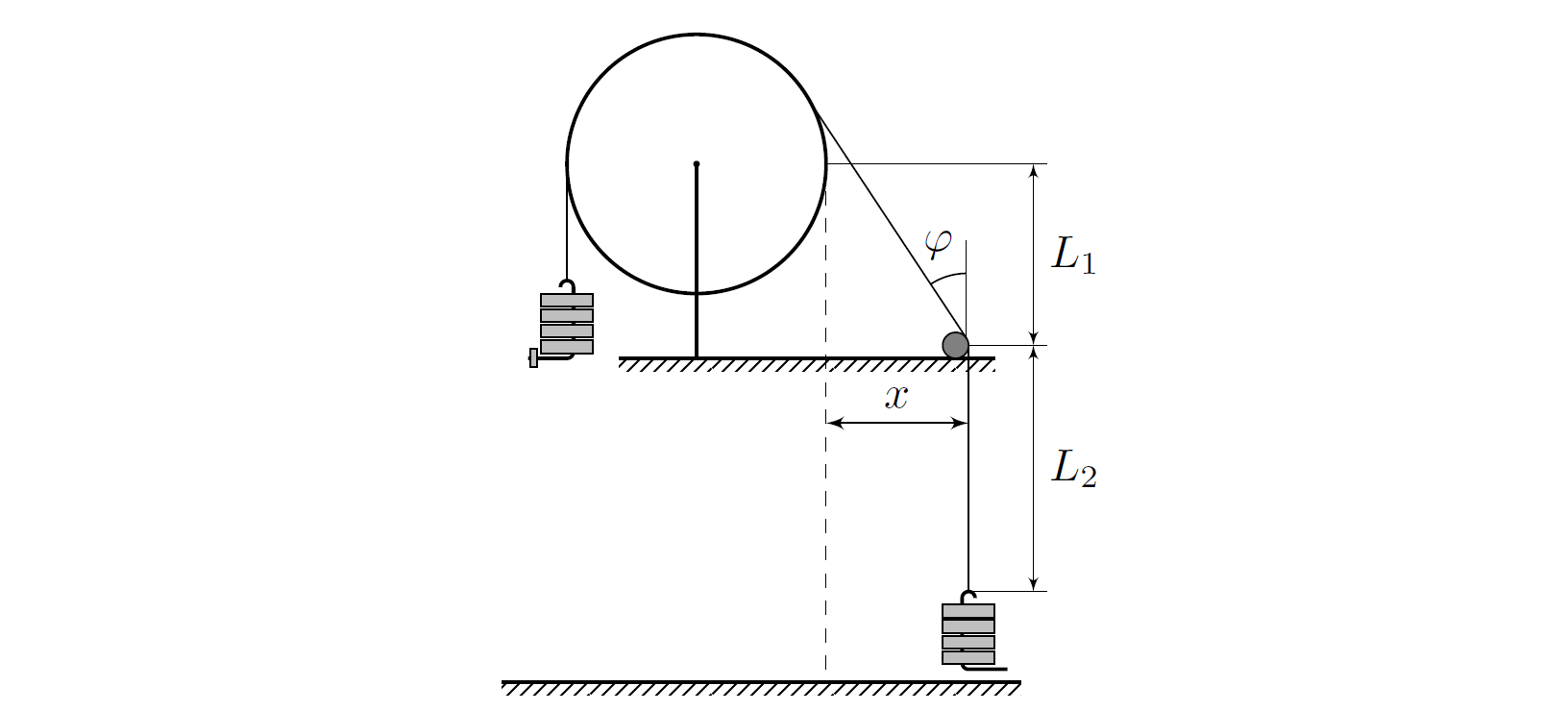
Зафиксируем $m_1 = 5M + 5m$, $m_2 = 5M$. При разных расстояниях $x$ будем измерять время $t$, за которое меньший грузик проходит расстояние $L_2=(66{,}0\pm0{,}2)~\text{см}$ от пола до карандаша.
\begin{equation}
(m_1 + m_2 + m_\text{эфф})a = (m_1 - m_2)g - \frac{m_1 + m_2}{2} \mu \varphi g.
\tag{5}
\end{equation}
Измерим расстояние $L_1=(47{,}5\pm0{,}1)~\text{см}$ от карандаша до боковой поверхности блока и радиус блока $r=(4{,}9 \pm 0{,}1)~\text{см}$. В нашем случае $\text{tg} \varphi \approx x/L_1$.
\[ \left(1 + \frac{m_\text{эфф}}{m_1+m_2} \right) \frac{2a}{g} = 2\frac{m_1-m_2}{m_1+m_2} - \mu \varphi, \]
где $a=2L_2/\langle t \rangle^2$. Построим график в координатах $Y_2=\left(1+\dfrac{m_\text{эфф}}{m_1+m_2} \right) \dfrac{2a}{g}$ от $\varphi$. Ему соответствует линейная зависимость:
\[ Y_2 = 2\frac{m_1-m_2}{m_1+m_2} - \mu \varphi. \]
Возможен другой метод решения, точность которого хуже. Будем двигать карандаш по горизонтали, пока нить не перестанет по нему скользить, и запишем расстояние $x$, соотвествующее этому моменту. В каждом эксперименте будем использовать $m_1 = N_\text{б} M + m_\text{м} m+m_\text{с}$, $m_2 = N_\text{б} M +m_\text{с}$.
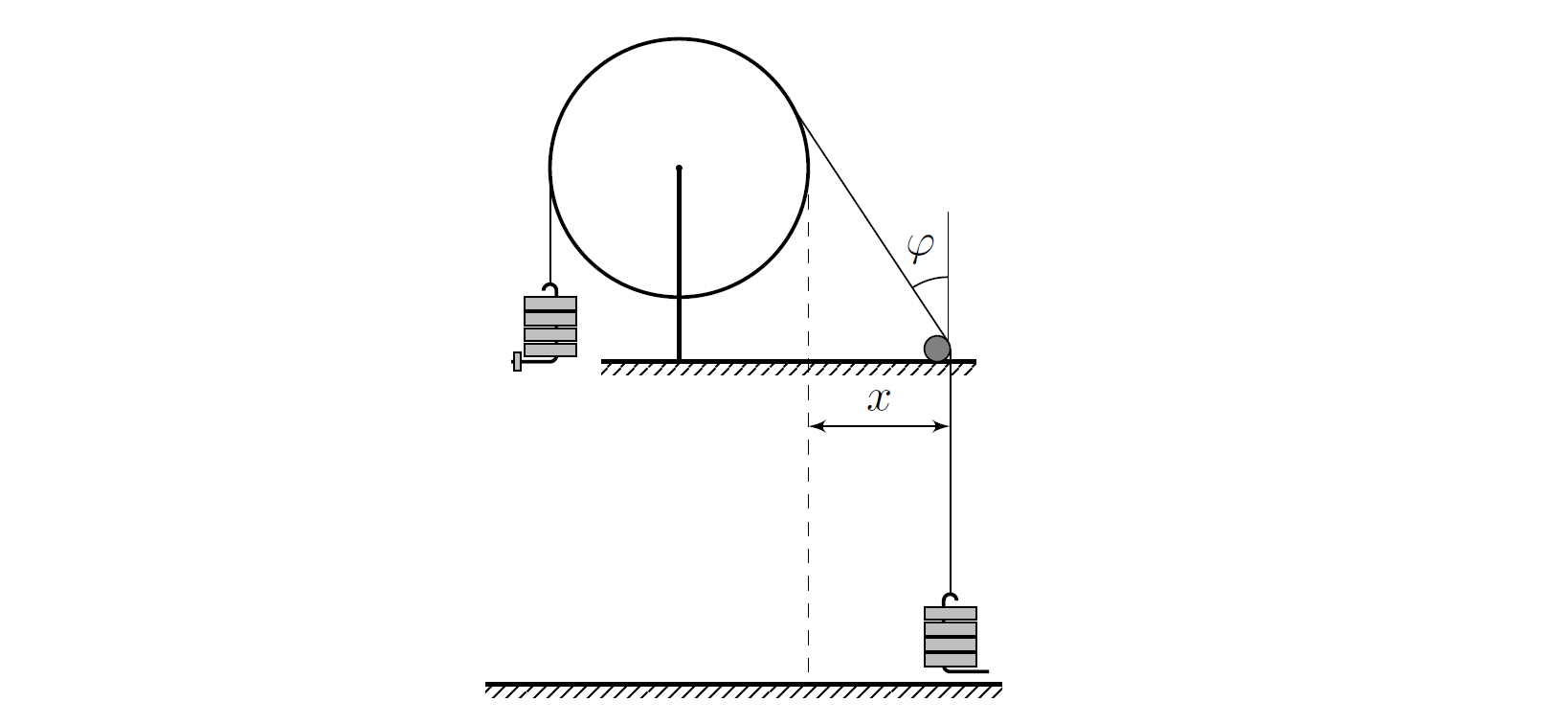
\[ \mu\,\text{arctg} \, x/L_1 = 2\frac{m_1 - m_2}{m_1+m_2}.\]
Построим график $Y_3=2\dfrac{m_1-m_2}{m_1+m_2}$ от $\varphi$. Он должен оказаться линейным, проходить через точку $(0,0)$ и иметь угловой коэффициент $k_3=\mu$. Формулы для пересчета:
\[ \varphi = \text{arctg} \, \langle x \rangle / L_1, \quad \langle x \rangle = \frac{1}{3} (x_1 + x_2 + x_3).\]