Покажем, что годограф вектора скорости является окружностью, причём отношение расстояния от начала отсчёта до центра окружности является эксцентриситетом орбиты.
Рассмотрим частицу массой $m$ в центральном поле с потенциальной энергией $U=-\alpha/r$. Запишем второй закон Ньютона и выражение для момента импульса частицы:
$$m\vec{a}=-\cfrac{\alpha\vec{e}_r}{r^2}\qquad \vec{L}=mr^2\vec{\omega}
$$
откуда:
$$\bigl[\vec{a}\times\vec{L}\bigr]=-\alpha\bigl[\vec{e}_r\times\vec{\omega}\bigr]=\alpha\bigl[\vec{\omega}\times\vec{e}_r\bigr]=\alpha\dot{\vec{e}}_r
$$
Интегрируя по времени, получим:
$$\cfrac{\bigl[\vec{v}\times\vec{L}\bigr]}{\alpha}-\vec{e}_r=\vec{e}
$$
где $\vec{e}$ - постоянный вектор, называемый вектором эксцентриситета.
Рассмотрим скалярное произведение с радиус-вектором $\vec{r}$ обеих частей уравнения:
$$\bigl(\vec{e}\cdot\vec{r}\bigr)=er\cos\varphi=-r+\cfrac{\bigl(\vec{r}\cdot\bigl[\vec{v}\times\vec{L}\bigr]\bigr)}{\alpha}=-r+\cfrac{\bigl(\vec{L}\cdot\bigl[\vec{r}\times\vec{v}\bigr]\bigr)}{\alpha}
$$
В последнем переходе мы воспользовались свойством чётной перестановки в смешанном произведении. Учитывая, что $\bigl[\vec{r}\times\vec{v}\bigr]=\vec{L}/m$, получим:
$$er\cos\varphi=-r+\cfrac{L^2}{\alpha m}\Rightarrow r(\varphi)=\cfrac{L^2}{\alpha m(1+e\cos\varphi)}
$$
Таким образом, модуль вектора $\vec{e}$ действительно является эксцентриситетом орбиты.
Рассмотрим векторное произведение $\bigl[\vec{L}\times\vec{e}\bigr]$:
$$\bigl[\vec{L}\times\vec{e}\bigr]=\cfrac{\bigl[\vec{L}\times\bigl[\vec{v}\times\vec{L}\bigr]\bigr]}{\alpha}-\bigl[\vec{L}\times\vec{e}_e\bigr]=\cfrac{\vec{v}L^2}{\alpha}-\bigl[\vec{L}\times\vec{e}_e\bigr]
$$
Здесь при раскрытии двойного векторного произведения мы воспользовались тем, что $\vec{v}\perp\vec{L}$. Далее, вводя орты цилиндрической системы координат, получим:
$$\vec{v}=\cfrac{\alpha}{L}\left(\bigl[\vec{e}_z\times\vec{e}_r\bigr]+\bigl[\vec{e}_z\times\vec{e}\bigr]\right)=\cfrac{\alpha\vec{e}_\varphi}{L}+\cfrac{\alpha\bigl[\vec{e}_z\times\vec{e}\bigr]}{L}
$$
Поскольку $\bigl[\vec{e}_z\times\vec{e}\bigr]$ - постоянный вектор, модуль которого равен $e$, годограф вектора скорости при Кеплеровом движении действительно является окружностью, расстояние от начала отсчёта до центра которой в $e$ раз больше, чем её радиус.

Далее имеет смысл рассматривать только эллиптические орбиты.
Зафиксируем радиус окружности $R=\alpha/L$, положение её центра в точке $O$ и положение конца вектора скорости $\vec{v}_1$ (он в $\alpha>1$ раз больше по модулю) в точке $A$. Тогда, поскольку соотношения между $\vec{v}_1$, $\vec{v}_2$ и $\vec{v}_\text{отн}$ (т.е отношения модулей и углы между векторами) сохраняются и поскольку конец вектора $\vec{v_2}$ описывает окружность радиуса $R$ с центром в точке $O$- начало отсчёта векторов скорости также описывает некоторую окружность радиусом $R_1$ с центром $O_1$, которая может быть получена из окружности радиусом $R$ гомотетией относительно точки $A$ и последующим поворотом. Выражение для коэффициента гомотетии $k$ и угла поворота $\varphi$ следующие:
$$k=\cfrac{\alpha}{\sqrt{\alpha^2+1}}\qquad \varphi=\arccos\cfrac{\alpha}{\sqrt{\alpha^2+1}}
$$

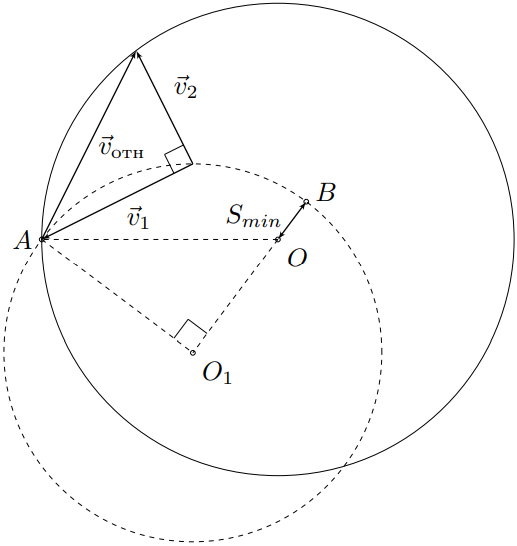
Минимальное расстояние от точки на окружность с центром в точке $O_1$ до точки $O$ минимально для такой точки $B$, что она лежит на прямой, проходящей через $O$ и $O_1$. Тогда имеем:
$$\cfrac{S_{min}}{R}=\cfrac{R_1-O_1O}{R}=\cfrac{\alpha}{\sqrt{\alpha^2+1}}-\cfrac{1}{\sqrt{\alpha^2+1}}=\cfrac{\alpha-1}{\sqrt{\alpha^2+1}}
$$
Поскольку по условию $\alpha=2$, находим:

Примечание: Обратите внимание, что изложенный способ решения легко позволяет обобщить результат для произвольного угла между скоростями $\vec{v}_1$ и $\vec{v}_2$, поскольку треугольник $\triangle O_1OA$ всегда будет подобен треугольнику, образованного скоростями $\vec{v}_1$, $\vec{v}_2$ и $\vec{v}_\text{отн}$.