
В этой задаче рассматривается один из эффектов общей теории относительности (далее ОТО) – теории, описывающей релятивистскую гравитацию. Оказывается, гравитация действует не только на обычные тела, но и на свет. Луч света отклоняется, проходя вблизи массивного тела.
Этот эффект послужил одним из первых подтверждений ОТО в 1919 г.
A1
1.00
Рассмотрим звезду массы $M$. Пусть мимо нее пролетает тело малой массы, имевшее первоначально большую (но нерелятивистскую) скоростью $v$, причем $v^2\gg{GM/R}$, где $R$ – наименьшее расстояние между центрами тел в процессе полета. Найдите угол, на которое оно отклонится от первоначального направления.
A2
0.30
Теперь рассмотрите фотон, летящий со скоростью света $c$. Для него верно соотношение $E=pc$, где $E$, $p$ – энергия и импульс фотона. Считайте, что гравитационная сила, действующая на фотон, определяется законом всемирного тяготения, где вместо массы используется величина $E/c^2$. Найдите угол отклонения $\delta$ фотона.
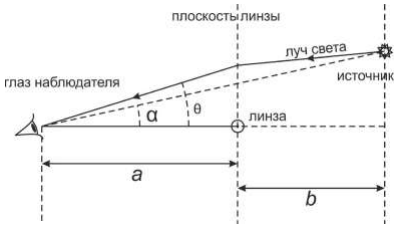
Наблюдатель видит свет от далекой звезды (назовем ее источником), который по пути проходит мимо другой звезды, назовем ее «линзой». Считайте известными расстояния $a$ и $b$.
B1
1.00
Предполагая вначале, что Земля, источник света и центр линзы находятся на одной прямой ($\alpha=0$), найдите угол $\theta_0$, под которым свет приходит к наблюдателю. Что видит наблюдатель в этом случае?
Угол $\theta_0$ называется углом Хвольсона-Эйнштейна по имени людей, разработавших теорию линзирования.
B2
0.50
Найдите численное значение $\theta_0$ (в угловых секундах), считая массы звезд источника и линзы равными массе Солнца $2\cdot{10^{30}~\text{кг}}$, радиусы равными радиусу Солнца $R=7\cdot{10^8}~\text{м}$, расстояния $a=b=10~\text{кпк}$. Один парсек равен $1~\text{пк}=3\cdot{10^{16}}~\text{м}$, скорость света $c=3\cdot{10^8}~\text{м}/\text{с}$, гравитационная постоянная $G=6{.}67\cdot{10^{-11}}~(\text{Н}\cdot{м}^2)/\text{кг}^2$.
По аналогии с отклонением лучей света обычной линзой данное явление принято называть «гравитационным линзированием». Однако это просто распространенный жаргон. Ничего общего с обычной тонкой линзой гравитационное линзирование не имеет. Аналогии с геометрической оптикой неприменимы!
В дальнейшем рассматривается общий случай $\alpha\neq{0}$. Плоскость, перпендикулярную плоскости рисунка и проходящую через звезду-линзу перпендикулярно прямой наблюдатель-линза, назовем плоскостью линзы. Всегда считайте, что изображения находятся в плоскости линзы.
B7
0.50
Пусть источник имеет малые, но ненулевые размеры. Зная $\Gamma_\perp$ и $\Gamma_\parallel$, найдите полное увеличение гравитационной линзы $\Gamma$. По определению это отношение площади изображения (лежащего в плоскости линзы) к площади проекции источника на плоскость, перпендикулярную лучу зрения.
B8
1.50
Как известно, собирающая линза фокусирует лучи, увеличивая поток энергии. Таким же свойством обладает гравитационная линза. Пусть в отсутствие линзы телескоп наблюдателя принимает от источника поток энергии $N_0~\left[\text{Вт}\right]$. Найдите, во сколько раз $\mu$ увеличивает линза принимаемый поток энергии. Световой поток от звезды – линзы считайте пренебрежимо малым. Считайте, что наблюдатель видит все возможные изображения ($\alpha\neq{0}$) и суммирует потоки энергии от них.
Обычно линзирование наблюдают, когда источником света и линзой служат не звезды, а галактики или скопления галактик, чьи массы огромны. Получающийся угол $\theta_0$ может в таких случаях составляет порядка $1$ угловой секунды, что доступно для наблюдения оптическими телескопами. Но для случая линзирования звезда-звезда в нашей галактике (называемого также микролинзированием угол $\theta_0$ так мал, что «разрешить» картину линзирования, т.е.
увидеть отдельно линзу и изображения, оптическими средствами не представляется возможным. Этого можно добиться только с помощью системы из нескольких радиотелескопов, которая является интерферометром с огромной базой и может измерять очень малые углы.
C1
1.00
Однако все же можно наблюдать микролинзирование на оптических телескопах. Для этого нужно измерять поток энергии от звезд, который, как мы выяснили, изменяется при линзировании, когда одна звезда проходит сзади другой. Процесс линзирования звезд в Галактике длится примерно $\tau=40~\text{дней}$. Если за это время мы пронаблюдаем звезду хотя бы
однажды, то, зная ее стандартную светимость, мы поймем, что наблюдаем гравитационное линзирование. Считайте, что в нашей Галактике $N=2\cdot{10^{11}}$ звезд, их массы примерно равны массе Солнца, характерный размер Галактики $L=10~\text{кпк}$. Оцените, сколько звезд $N_0$ нужно наблюдать ежемесячно, чтобы за $t=1~\text{год}$ найти $k=10$ событий гравитационного линзирования.