
Без электрического поля уравнение движения
$$
\ddot{y} = -\omega_0^2 y,
$$
после добавления электрического поля получим
Подставив в уравнение $y = y_0 \cos \omega t$, получим
$$
- \omega^2 y_0 = - \omega_0^2 y_0 - \frac{qE_0}{m},
$$
откуда
Моделируем атом как неподвижный положительный заряд $q$, окруженный сферическим отрицательно заряженным облаком с полным зарядом $-q$, радиус $r$, масса $m$. Пусть облако смещается на малое расстояние $y$. Электростатическая сила, действующая на облако со стороны заряда
$$
\vec{F}_{el} = m\ddot{y} \hat {y} = - \frac{q^2}{4 \pi \varepsilon_0 r^3} y \hat{y} = -m \omega_0^2 y\hat{y}.
$$
Тогда собственная частота колебаний
Запишем размерности величин, входящих в формулу для мощности излучения
\begin{align}
& [s] = кг \cdot м^2 \cdot с^{-3}\\
&[p_0] = Кл \cdot м\\
&[\omega] = c^{-1} \\
& [\varepsilon_0 ] = Кл^2 \cdot кг^{-1} \cdot м^{-3} \cdot с^2\\
&[c]= м \cdot с^{-1}
\end{align}
Пусть формула для мощности имеет вид $s = p_0^\alpha \omega^\beta \varepsilon_0^\gamma c^\delta$. Приравнивая размерности, получим следующие уравнения:
\begin{align}
&\alpha + 2 \gamma = 0;\\
& \gamma = -1;\\
& -\beta + 2 \gamma -\delta = -3;\\
& \alpha - 3 \gamma + \delta = 2.
\end{align}
Из них находим
$$
\alpha = 2;\; \beta = 4;\; \gamma = -1;\; \delta = -3.
$$
Интенсивность — мощность, проходящая через единицу площади. Рассмотрим горизонтальный цилиндр в атмосфере, площадь поперечного сечения $A$, длина $\Delta x$. Пусть падающая интенсивность $I(x)$, а выходящая интенсивность $I(x + \Delta x)$. Интенсивность уменьшается за счет того, что свет рассеивается молекулами воздуха. Если концентрация молекул $n_0$, полная мощность излучения на единицу объема равна $n_0 s$. Поэтому
$$
I(x) A - I(x+ \Delta x) A = n_0 s(A \Delta x).
$$
Отсюда находим
Поскольку мощность излучения $s$ пропорциональна $E_0^2$ а интенсивность света $I$ также пропорциональна $E_0^2$, получаем
$$
- \frac{dI}{dx} = \frac{I}{L},
$$
где $L$ — некоторая постоянная с размерностью длины, которую можно найти из выражений для $I$ и $s$:
$$
L = \frac{6 \pi \varepsilon_0^2 m^2 c^4}{n_0 q^4} \left( \frac{\omega_0}{\omega}\right)^4.
$$
Решение уравнения на интенсивность
$$
I = I_0 e^{- x/L}
$$
Подставим числа в общую формулу и получим
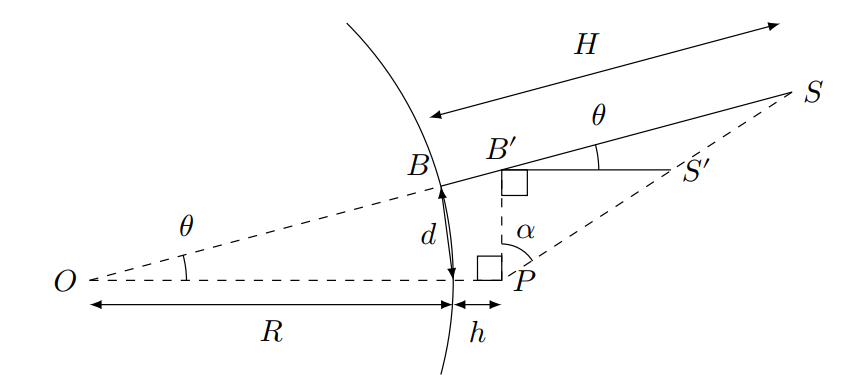
В $\Delta OP B^\prime$
$$
OB^\prime = \frac{OP}{\cos \theta} = \frac{R + h}{\cos \theta}.
$$
Поскольку $\angle OSP = \angle B^\prime S S^\prime$ и $\angle SOP = \angle S B^\prime S^\prime$, треугольники $\Delta OSP$ и $\Delta B^\prime S S^\prime$ подобны, откуда
$$
\frac{B^\prime S^\prime}{OP} = \frac{B^\prime S}{O S} = \frac{OS - OB^\prime}{OS} = 1 - \frac{OB^\prime }{OS}.
$$
Заметим, что $B^\prime S^\prime = H^\prime$, $OP = R + h$, $OS = R + H$. Используя выражение для $OB^\prime$, получим
$$
\frac{H^\prime}{R + h} = 1 - \frac{R + h}{(R + H) \cos \theta}
$$
$$
H^\prime = R + h - \frac{(R + h)^2}{R + H} \frac{1}{\cos \theta}.
$$
С учетом малости угла $\theta = d/R$ можно использовать $\cos \theta \approx 1 - \theta^2/2$, поэтому
В уравнении $I = I_0 e^{-x/L}$ $I_0$ означает интенсивность источника, которую наблюдатель бы видел в данной точке, если бы не было затухания. Если мощность источника равна $P_0$, тогда $I_0 = P_0/(4 \pi d^2)$ для источника на расстоянии $d$.
$$
I = \frac{P_0}{4 \pi d^2} e^{-d /L}
$$
Относительная яркость Эвереста (для наблюдателя в Дарджилинге):
Из размерности и информации в условии находим
$$
L_p = \frac{1}{8 n \pi r^2}.
$$
Концентрацию можно связать с плотностью аэрозоля и массой одной частицы аэрозоля. Массу в свою очередь можно выразить через плотность и радиус
$$
n = \frac{\rho_p}{m}, \quad m = \frac{4 \pi}{3} r^3 \rho.
$$
Отсюда находим
Новое выражение для интенсивности (с учетом двух вкладов в затухание)
$$
I = \frac{P_0}{4 \pi d^2} \exp \left[ -\frac{d}{L} - \frac{d}{L_p}\right].
$$
Для горы Канченджанга
$$
\frac{I_K}{I_{ref}} = \exp \left[ - \frac{d_K}{L_p} \right] = 0.22
$$
Это больше 5%, поэтому гора будет видима.
Для Эвереста
$$
\frac{I_E}{I_{ref}} = 0.093 \exp \left[ - \frac{d_E}{L_p} \right] = 0.003,
$$
поэтому Эверест не видно.