
Рассмотрим общий случай, в котором движутся как детектор (скорость $v_d$), так и источник (скорость $v_s$). Также линия, соединяющая источник с детектором, образует угол $\alpha$ с осью $x$ (как на рисунке 1 в условии).
Заметим, что $\alpha$ зависит от времени. Пусть $\hat{n}$ обозначает единичный вектор, направленный от источника к детектору. Для случая, когда источник приближается к детектору, регистрируемая частота равна
\begin{align}
f(t^\prime)& = f_0 \frac{c - \vec{v}_d \hat{n}}{c - \vec{v}_s \hat{n}} =
f_0 \frac{c - v_d \cos (\gamma - \alpha(t))}{c - (\vec{v}_s + R\omega\hat{\theta}) \hat{n}} =
f_0 \frac{c - v_d \cos (\gamma - \alpha(t))}{c - [v_s \cos(\beta - \alpha(t)) + R \omega \cos(\omega t + \phi + \pi/2 - \alpha(t))]} \\
&= f_0 \frac{c - v_d \cos (\gamma - \alpha(t))}{c - [v_s \cos(\beta - \alpha(t)) - R \omega \sin(\omega t + \phi - \alpha(t))]}
\end{align}
Аналогично для случая, когда источник удаляется от детектора
$$
f(t^\prime) = f_0 \frac{c - v_d \cos (\gamma - \alpha(t))}{c +[v_s \cos(\beta - \alpha(t)) - R \omega \sin(\omega t + \phi - \alpha(t))]}
$$
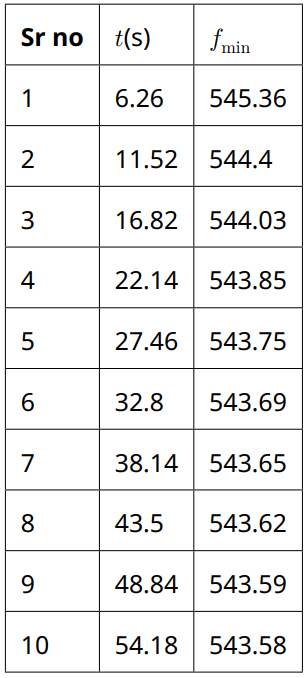
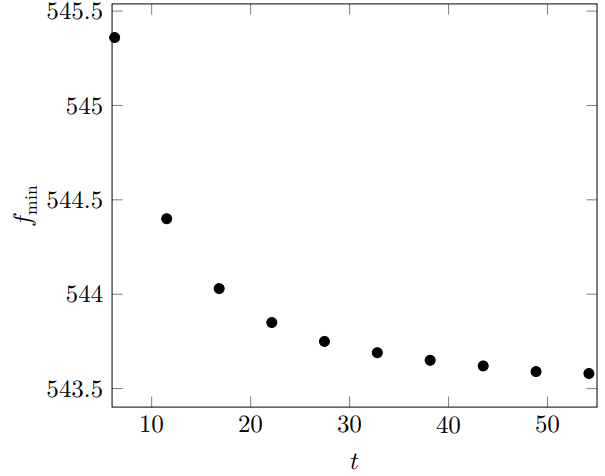
Минимальная частота в пределе $t \to \infty$
Найдем начальное положение источника. Для этого сначала поместим детектор в точку на оси $x$ с координатой $x_1$ (параметры положения детектора $x_1, \, 0^\circ$), а затем — на оси $y$ с координатой $y_1$ (параметры $y_1, \, 90^\circ$ ). Из графика, запишем момент времени, в который первый сигнал достиг детектора. Обозначим соответственные времена $\Delta t_x$ и $\Delta t_y$ соответственно. Тогда
\begin{align}
(x- x_1)^2 + y^2 = (c \Delta t _x)^2, \\
x^2 + (y - y_1)^2 = (c \Delta t _y)^2.
\end{align}
Решение этой системы даст координаты источника. Например можно использовать значения $x_1 = 500~м$, $\Delta t_x = 1.5344~с$ и $y_1 = 500~м$, $\Delta t_y = 1.2727~c$. У каждого из двух уравнений выше есть два решения. Правильное решение можно выбрать, используя детектор в некотором третьем положении. Окончательно, получим
Пусть детектор находится в таком положении, где источник сначала приближается к нему с большого расстояния (например слева), а затем проходит мимо него и удаляется на большое расстояние (направо). В предельных случаях (далеко слева и далеко справа $\alpha \approx \beta$) можно измерить две пары частот — значения в максимуме и в минимуме (зависимость практически строго постоянна). Скорость детектора равна нулю $v_d = 0$.
Далеко слева
\begin{align}
f_{max} = f_0 \frac{c}{c - (v_s + \omega R)},\\
f_{min} = f_0 \frac{c}{c - (v_s - \omega R)}.
\end{align}
Далеко справа
\begin{align}
f_{max} = f_0 \frac{c}{c + (v_s - \omega R)},\\
f_{min} = f_0 \frac{c}{c + (v_s + \omega R)}.
\end{align}
Из первой пары частот (слева) находим
$$
\frac{f_{max} + f_{min}}{f_{max} - f_{min}} = \frac{c - v_s}{\omega R}.
$$
Из второй пары (справа)
$$
\frac{f_{max} + f_{min}}{f_{max} + f_{min}} = \frac{c + v_s}{\omega R}.
$$
Отметим также, что из-за изменения расстояния между источником и детектором интервал времени между соседними максимумами регистрируемой частоты отличается от периода движения детектора по окружности $2\pi/\omega$. В области, где детектор удаляется
$$
\Delta t = \frac{2 \pi}{\omega} \left( 1 + \frac{v_s}{c}\right).
$$
(Время увеличивается, поскольку более позднему импульсу нужно пройти большее расстояние, эффект полностью аналогичен эффекту Доплера.)
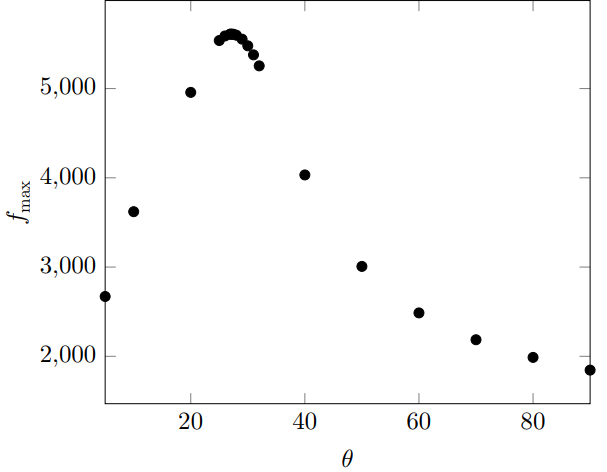
Полученные три уравнения можно использовать, чтобы определить $v_s$, $\omega$ и $R$. Для этого нужно расположить неподвижный детектор в таком положении, чтобы источник сначала приближался с него с большого расстояния, а затем удалялся. Предельные значения частот можно найти из тех участков графика, где значения максимумов практически не меняются со временем. Кроме того, мы ожидаем резкого изменения в графике в том случае, когда детектор расположен почти на пути источника, $\beta \approx \alpha$. Зафиксировав расстояние до детектора 8000 м, будем менять угол $\theta$.
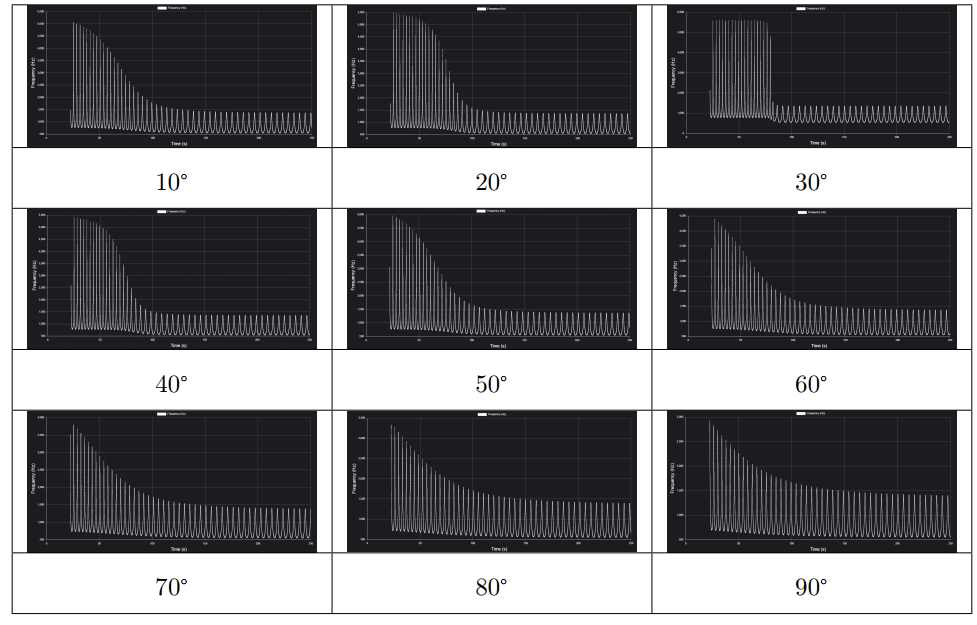
Видим, что при значении угла $\theta = 30^\circ$ на графике наблюдается наиболее выраженный переход к предельным режимам слева и справа. В этих случаях значения частоты в максимумах практически не зависят от времени. При этом значения на левой части графика больше, чем на правой. Это означает, что на правой стороне источник удаляется от детектора. Для более точных измерений можно построить интересующий нас участок графика с уменьшенным расстоянием между точками на графике.
На левой части графика $f_{min} = 788.24$ Гц, $f_{max} = 5569.59$ Гц, поэтому
$$
\frac{f_{max} + f_{min}}{f_{max} + f_{min}} = 1.33 = \frac{c - v_s}{\omega R}.
$$
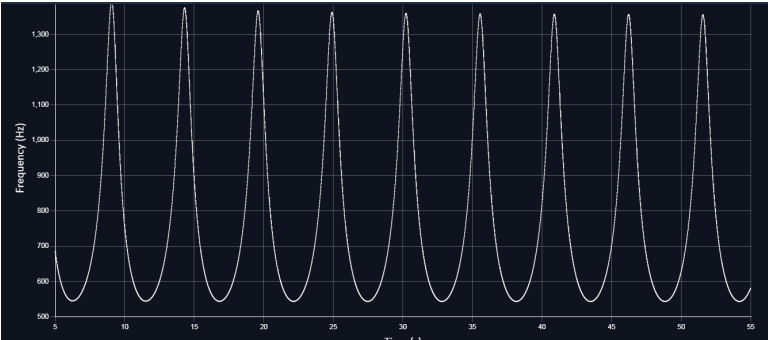
На правом участке $f_{min} = 543.06$ Гц, $f_{max} = 1353.45$ Гц. Поэтому
$$
\frac{f_{max} + f_{min}}{f_{max} + f_{min}} = 2.34 = \frac{c + v_s}{\omega R}.
$$
Отсюда находим $v_s = 91.1$ м/c, $\omega R = 179.66$ м/c. Расстояние между двумя максимумами при удаляющемся источнике $\Delta t = 5.36$ с. Отсюда получим $\omega = 1.49 \text{ с}^{-1}$. Поэтому $R = 120.57$ м. Для определения $f_0$ используем $f_{max}$ для удаляющегося источника. Тогда получим $f_0 = 990.26$ Гц.
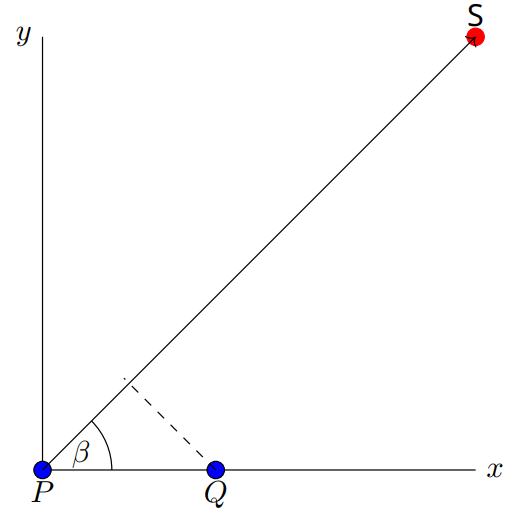
Пусть детектор находится на большом расстоянии от источника. Сигнал достигает детектора в точке $P$ за время $t_0 = 1009.61$ с, а до детектора в точке $Q$ за время $t_1 = 1007.85$ с. Расстояние между детекторами $PQ = 660$ м.
Разность этих времен можно найти как
$$
t_0 - t_1 = \frac{PQ \cos \beta}{c}.
$$
Отсюда
$$
\cos \beta = \frac{c (t_0 - t_1)}{PQ}.
$$
Отсюда получаем $\beta = 28.36^\circ$.
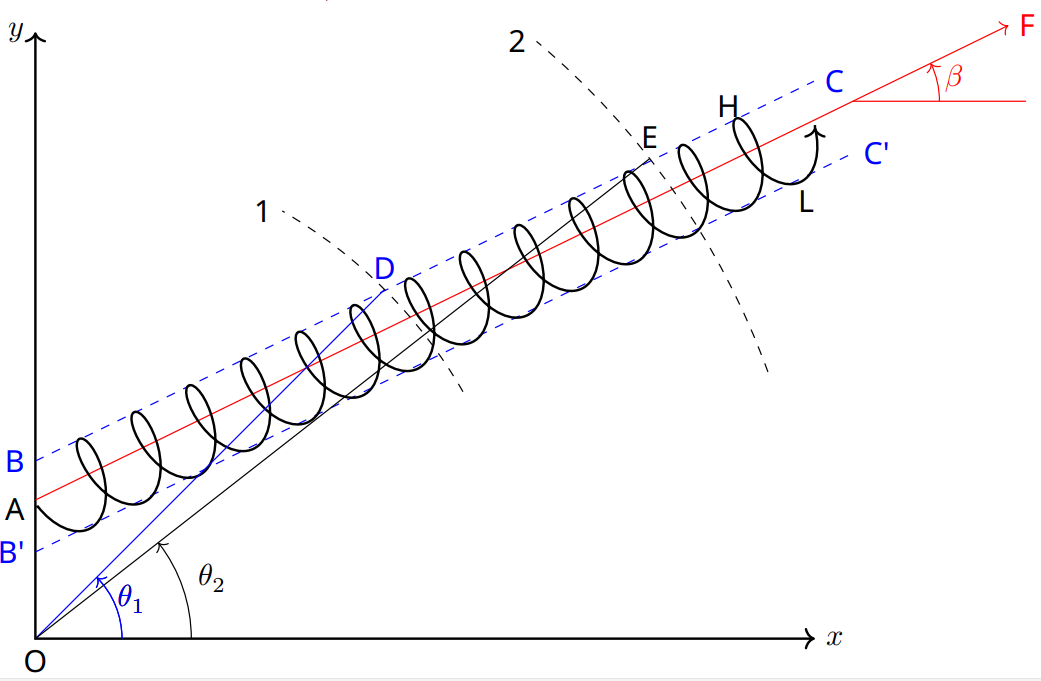
Значение зарегистрированной частоты зависит од двух факторов: от положения источника на циклоиде в момент испускания, и от положения детектора.
Точки $H$ и $L$ на одном периоде траектории обозначают места, где скорость источника максимальна и минимальна соответственно. Это следует из того, что скорость центра $\vec{v}_s$ тут параллельна или антипараллельна скорости движения по окружности.
Пусть источник совершает n-й поворот по циклоиде, а детектор расположен в некоторой точке дуги окружности 1, центр которой находится в начале координат. В зависимости от положения на дуге детектор будет регистрировать различные значения максимальной частоты $f_{max}$. Начнем от положения детектора вблизи оси $x$ ($\theta = 0^\circ$). Будем изменять угол, частота $f_{max}$ будет возрастать до того момента, когда детектор попадет в точку $D$ (этому отвечает некоторое значение угла $\theta_1$). На самом деле, для любого положения детектора на прямой $B C$, которая параллельна $AF$, он будет регистрировать максимально возможное значение максимума частоты $f_{max}$. Аналогично, в любой точке прямой $B^\prime C^\prime$, параллельной $AF$ будет детектироваться минимальное значение $f_{min}$ частоты в минимуме.
В симуляции мы будем менять положение детектора, а его скорость оставим равной нулю. Повторим это упражнение для детектора, который движется по другой дуге 2. Так мы найдем угол $\theta_2$, при котором максимум частоты принимает наибольшее значение.
Найдя два значения $\theta_1$ и $\theta_2$, мы можем использовать координаты точек $D$ и $E$, чтобы найти угол, который отрезок $DE$ образует с горизонтальной осью $x$. Это и есть искомый угол $\beta$. Если координаты точек $(x_1, \, y_1)$ и $(x_2, \, y_2)$ соответственно, угол
$$
\beta = \arctan \frac{y_2 -y_1}{x_2-x_1}.
$$
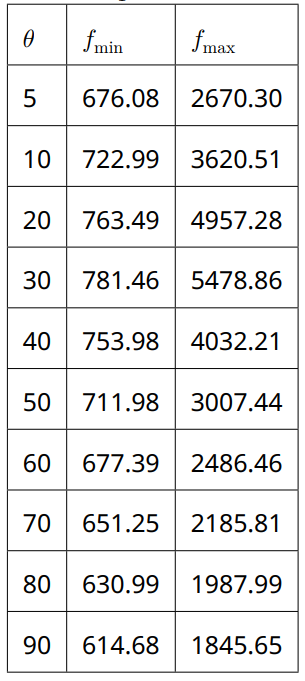
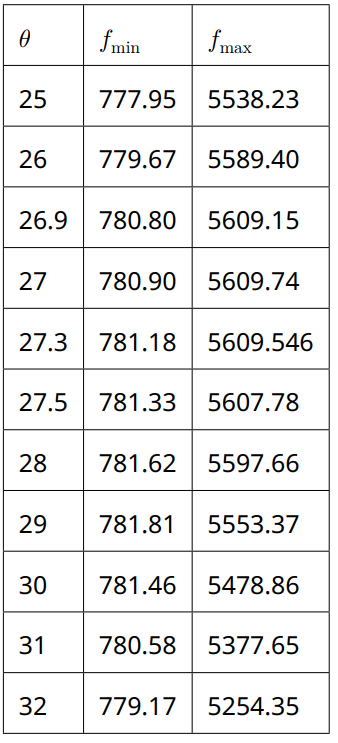
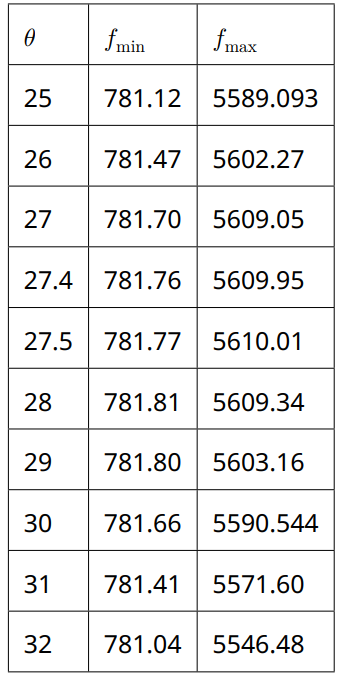
Из анализа первой таблицы следует, что максимум находится в диапазоне $\theta_1 \in (25^\circ, \, 35^\circ)$. Точное значение угла можно найти из графика, $f_{max}$ от $\theta$, получаем $\theta_1 = 27^\circ$.
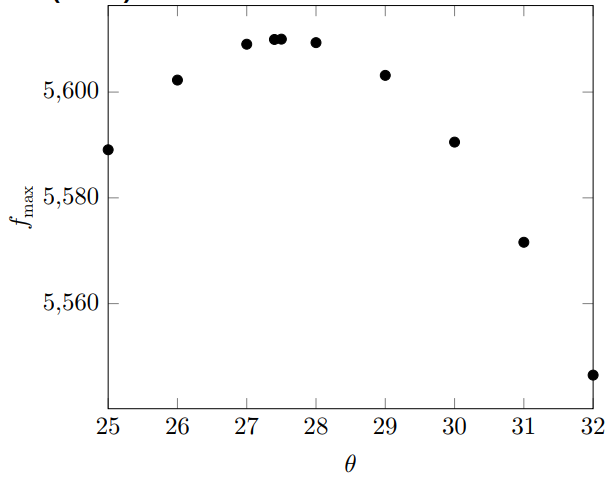
Из графика получаем, что для второй дуги максимум находится при $\theta_2 = 27.5^\circ$. Используя найденные значения углов, определим координаты детекторов, а отсюда и угол $\beta = 28.5^\circ$.
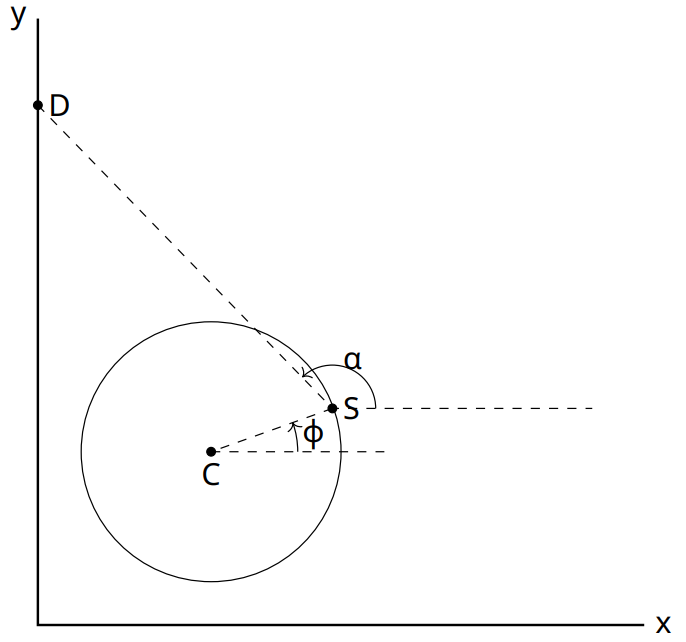
В этой части расположим детектор в некоторой точке на оси $y$. Найдем значение частоты для первого из сигналов, который получит детектор. Мы уже знаем значение $R$ и начальные координаты источника. Регистрируемая частота $f = 795.69$ Гц, если детектор расположен в точке $y = 500 $ м. Учитывая координаты источника (420 м, 500 м), значение угла $\alpha =180^\circ$. Используя эти значения угла и частоты, найдем:
$$
795.69 = \frac{990.26 \times 330}{330 - 91.1 \cos (28.5 - 180) + 179.66 \sin(\phi - \alpha)}.
$$
Отсюда найдем угол $\phi \approx 0^\circ$.
Тогда получаем координаты центра