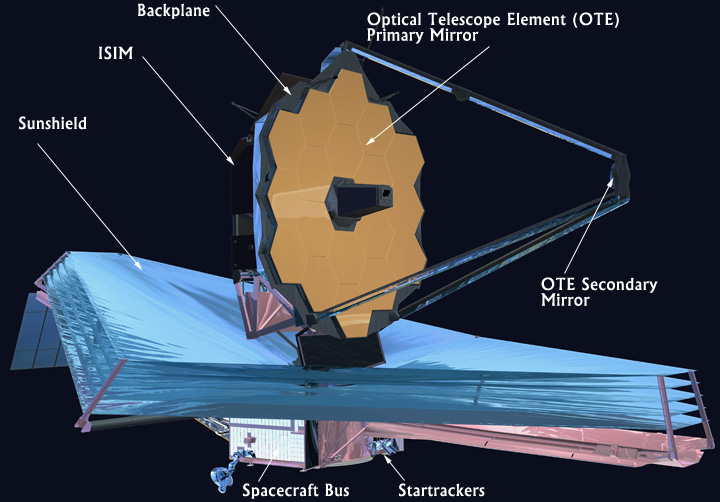
Данная задача посвящена физике космического телескопа "Джеймc Уэбб". Свет от звезды отражается от первичного зеркала с площадью $A_{\text{mirror}} = 25\,\mathrm{м^2}$, а затем отражается от вторичного зеркала. Фокусное расстояние системы $f = 130\,\mathrm{м}$. Свет фокусируется в ISIM, который содержит CCD камеру (charged-coupled device, прибор с зарядовой связью).

Часть A. Изображения звезд (1.8 балла)

Ближайший красный гигант расположен на расстоянии 89 световых лет и имеет температуру $T_{\mathrm{star}} = 3600\,\mathrm{K}$ и диаметр $d_o = 1.7\times 10^{11}\,\mathrm{м}$

A1  ^0.40 Вычислите диаметр сфокусированного изображения звезды на матрице CCD камеры.

A2  ^0.40 Оцените диаметр дифракционного максимума на матрице CCD камеры. Считайте, что длина волны $\lambda = 800\,\mathrm{нм}$ (наиболее интенсивная длина волны красного гиганта).

A3  ^1.00 Если CCD не охлаждается и может терять теплоту только из-за излучения с поверхности матрицы, какая будет установившаяся температура в области изображения красного гиганта? Считайте, что поверхность CCD матрицы является черным телом. Укажите формулу и вычислите.

Часть B. Счет фотонов (1.8 балла)

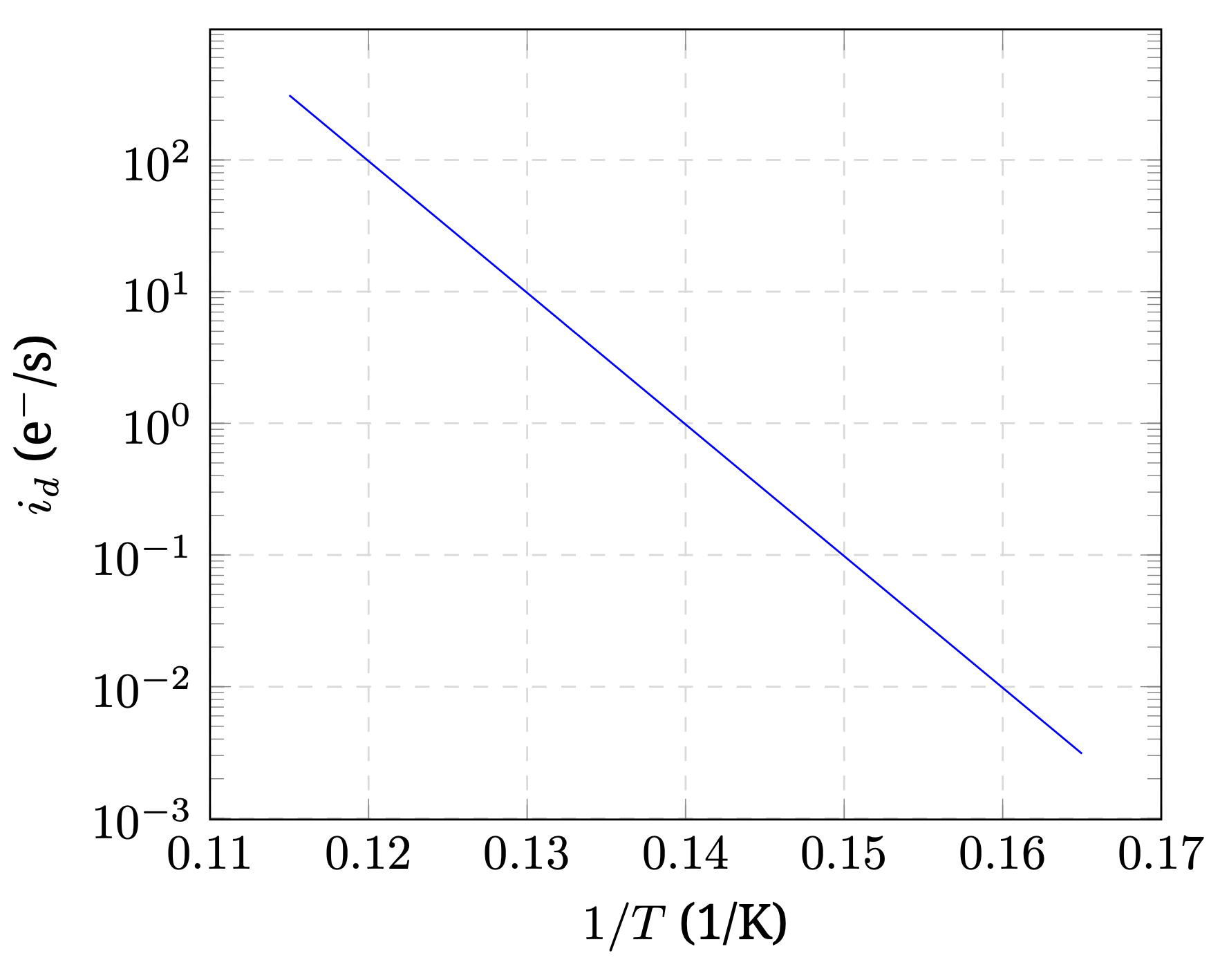
Поглощение фотона CCD камерой приводит к испусканию электрона внутри прибора. Это происходит, если у фотона имеется достаточная энергия для освобождения электрона через энергетический барьер $\Delta E_g$. Считайте, что каждый фотон с достаточной энергией приводит к появлению электрона. Существует просачивание электронов через энергетический зазор, связанная с температурой CCD камеры; этот процесс называется темновой ток (dark current) $i_d$, который измеряется в количестве электронов в секунду. Он зависит от температуры по формуле:

$$i_d = i_0 e^{-|\Delta E_{g}|/6 k_B T}.$$

где $i_0$ — некоторая константа.

B1  ^0.40 Используя график темнового тока, оцените по порядку температуру удалённого источника фотонов теплового излучения, которые смогут возбудить электроны в пикселях камеры.

Электроны накапливаются в конденсаторе, и по истечении времени экспозиции $\tau$ электроны считаются. В данном процессе есть три основных источника погрешностей: постоянная погрешность, которая называется шум считывания (read out noise); погрешность Пуассона, связанная с темновым током; погрешность Пуассона, связанная с детектированным потоком фотонов. Погрешность Пуассона для некоторого явления равна квадратному корню из числа событий этого явления.

Измеренное количество отсчетов фотонов равно количеству электронов в конденсаторе минус количество электронов, связанных с темновым током.

B2  ^0.40 Получите выражение для погрешности общего количества отсчетов $\sigma_t$, если известны шум считывания (read out noise) $\sigma_r$, темновой ток $i_d$, количество прилетов фотонов в секунду $p$, время экспозиции $\tau$.

Для следующих вопросов считайте, что время экспозиции $\tau=10^4~с$. Величина шума считывания (read out noise) $\sigma_r=14$.

B3  ^0.50 Считайте, что рабочая температура $T_{\mathrm{p}} = 7.5\,\mathrm{K}$. Вычислите минимальное количество прилета фотонов в секунду $p$ для случая, когда количество отсчетов фотонов в десять раз больше погрешности.

B4  ^0.50 Считайте, что все фотоны такие, что их только-только достаточно для возбуждения электронов через энергетический барьер. Чему в этом случае равна интенсивность источника фотонов из пункта B3 на первичном зеркале. Выразите ответ в $\mathrm{Вт/м^2}$.

Часть C. Зонт (4.4 балла)

Инфракрасная CCD камера должна использоваться при низких температурах. Для защиты от солнечного излучения используется "зонт", состоящий из 5 тонких пластин (на рисунке — черные), разделенных пустыми зазорами. Солнечное излучение (на рисунке — серое) падает слева на первую пластину.

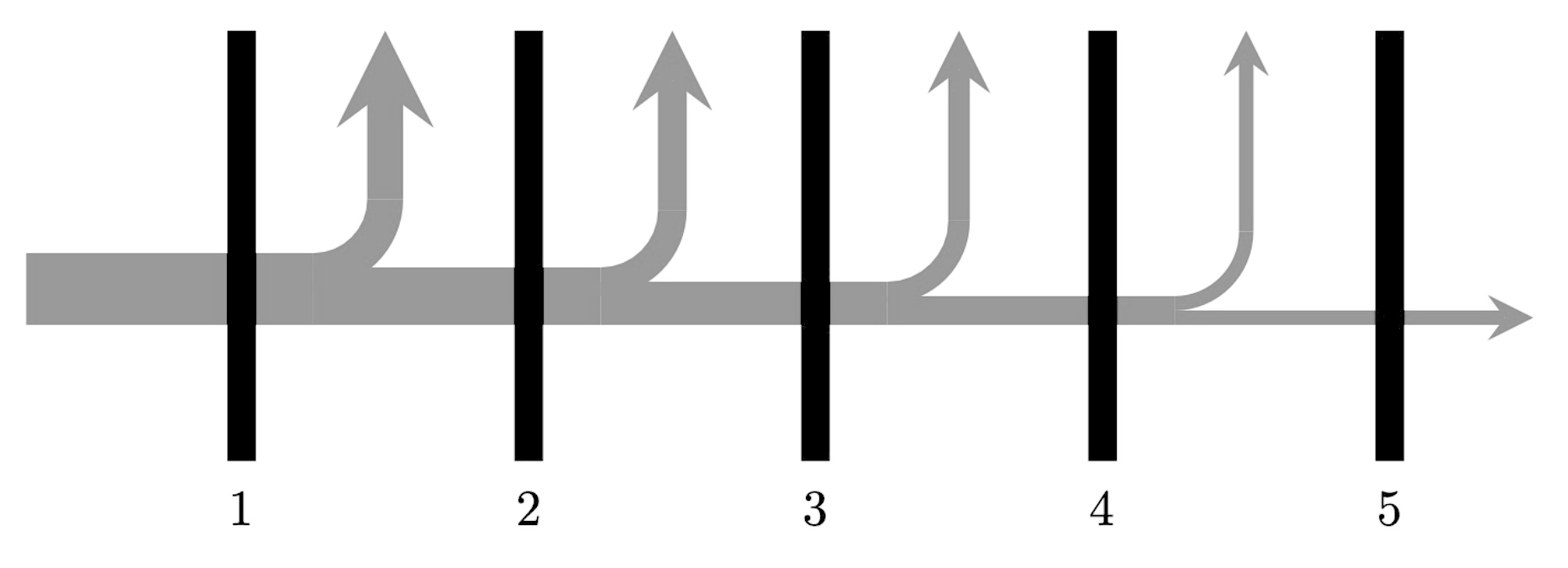
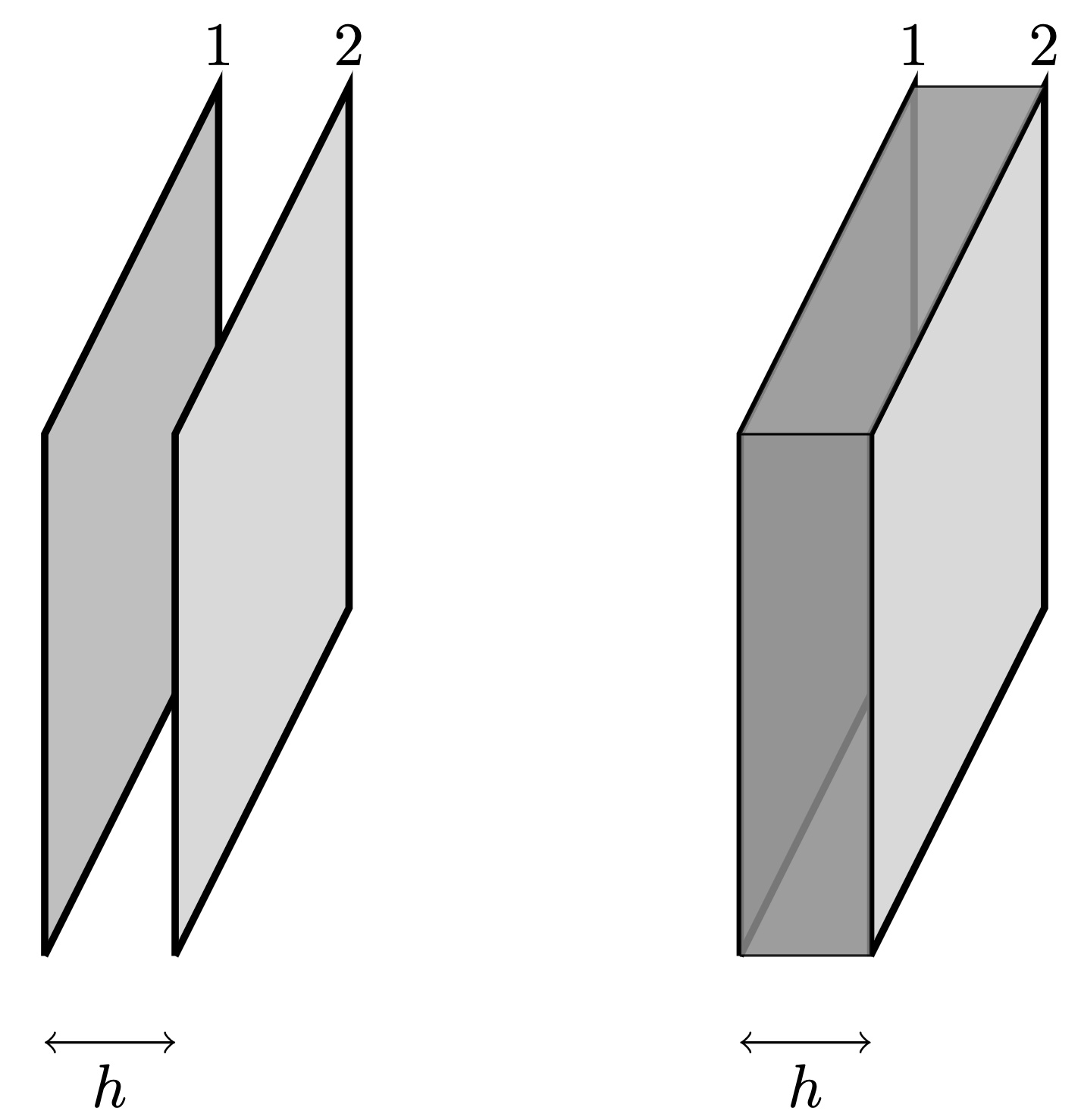
Для простоты будем считать, что:

• Каждая пластина «зонта» – квадрат площади $A_{sheet}=200~м^2$.
• Толщина промежутка между соседними пластинами всюду равна $h=25~см$.
• Пластины излучают рассеянный свет (диффузно). Поглощательная способность пластин («степень черноты») $\epsilon\ll 1$.
• Пластины тонкие, равномерно нагретые, температура каждой пластины одинакова на обеих ее поверхностях.
• Введем коэффициент $\alpha$ следующим образом. Пусть с правой поверхности пластины 1 (см. рисунок выше) была испущена энергия $Q_1$, а $\alpha Q_1$ — та доля этой энергии, которая оказалась поглощена пластиной 2, причем $\alpha\le 1$.
• Пусть $\alpha Q_{12}$ — полный поток энергии от пластины 1 к пластине 2. Тогда определим коэффициент $\beta < 1$ так, что потери энергии через закрашенную на правом рисунке область равны $\beta Q_{12}$ — эта энергия безвозвратно рассеивается в окружающий космос.
• Температура окружающего вакуума нулевая.

C1  ^2.40 Выразите равновесные температуры 1-й и 5-й пластин через $I_0$ (интенсивность падающего солнечного излучения) и константы $\alpha$ и $\beta$, а также любые необходимые физические постоянные. Для упрощения выражений можете любые комбинации величин $\alpha$ и $\beta$ обозначать как новые константы.

C2  ^1.60 Используя геометрические параметры пластин и считая их поглощательную способность равной $\epsilon = 0.05$, получите численные оценки для $\alpha$ и $\beta$.

C3  ^0.40 Рассчитайте численно температуры 1-й и 5-й пластин. Интенсивность солнечного излучения $I_0 = 1360\,\mathrm{Вт/м^2}$.

Часть D. Охлаждение камеры (4 балла)

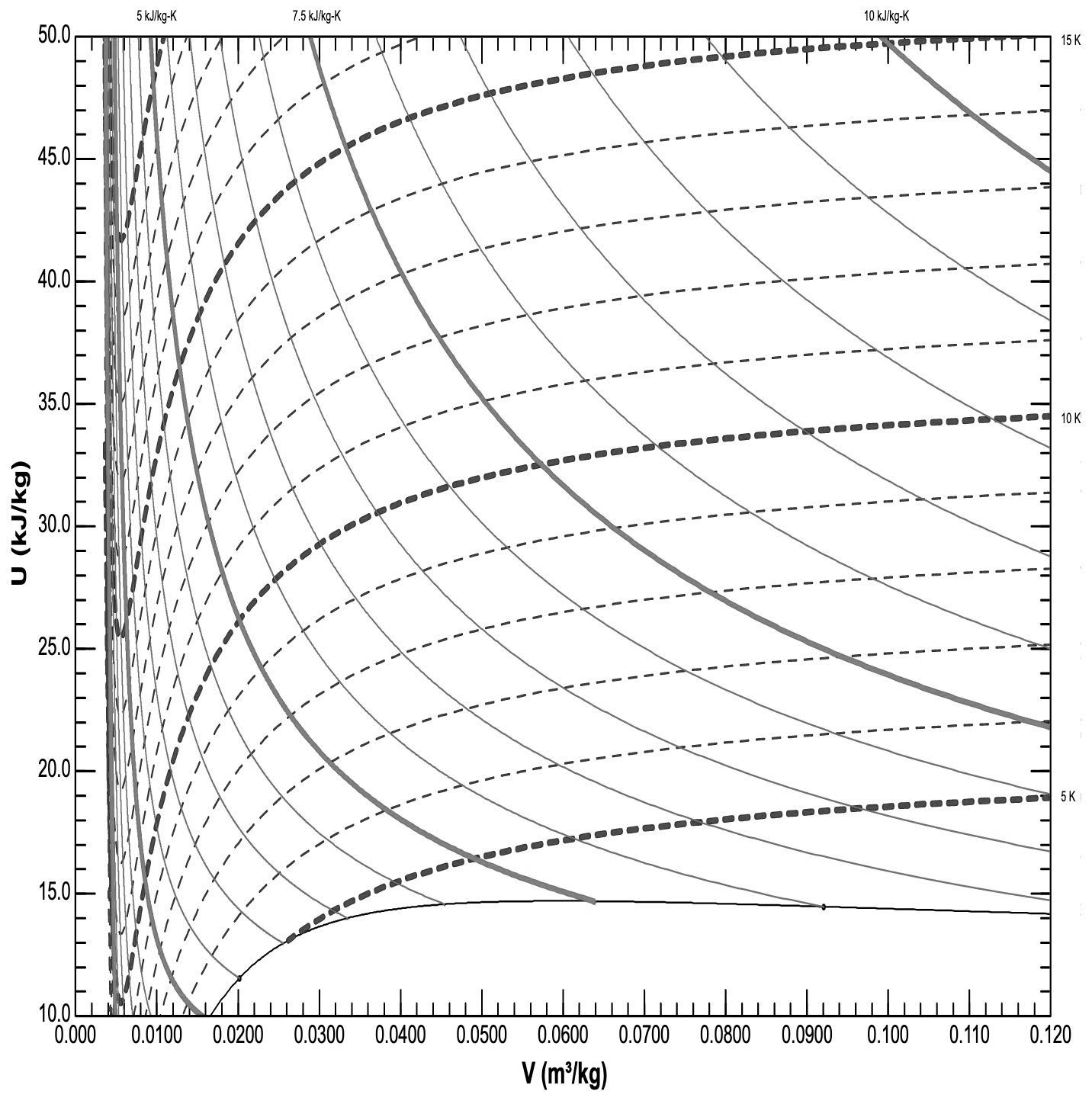
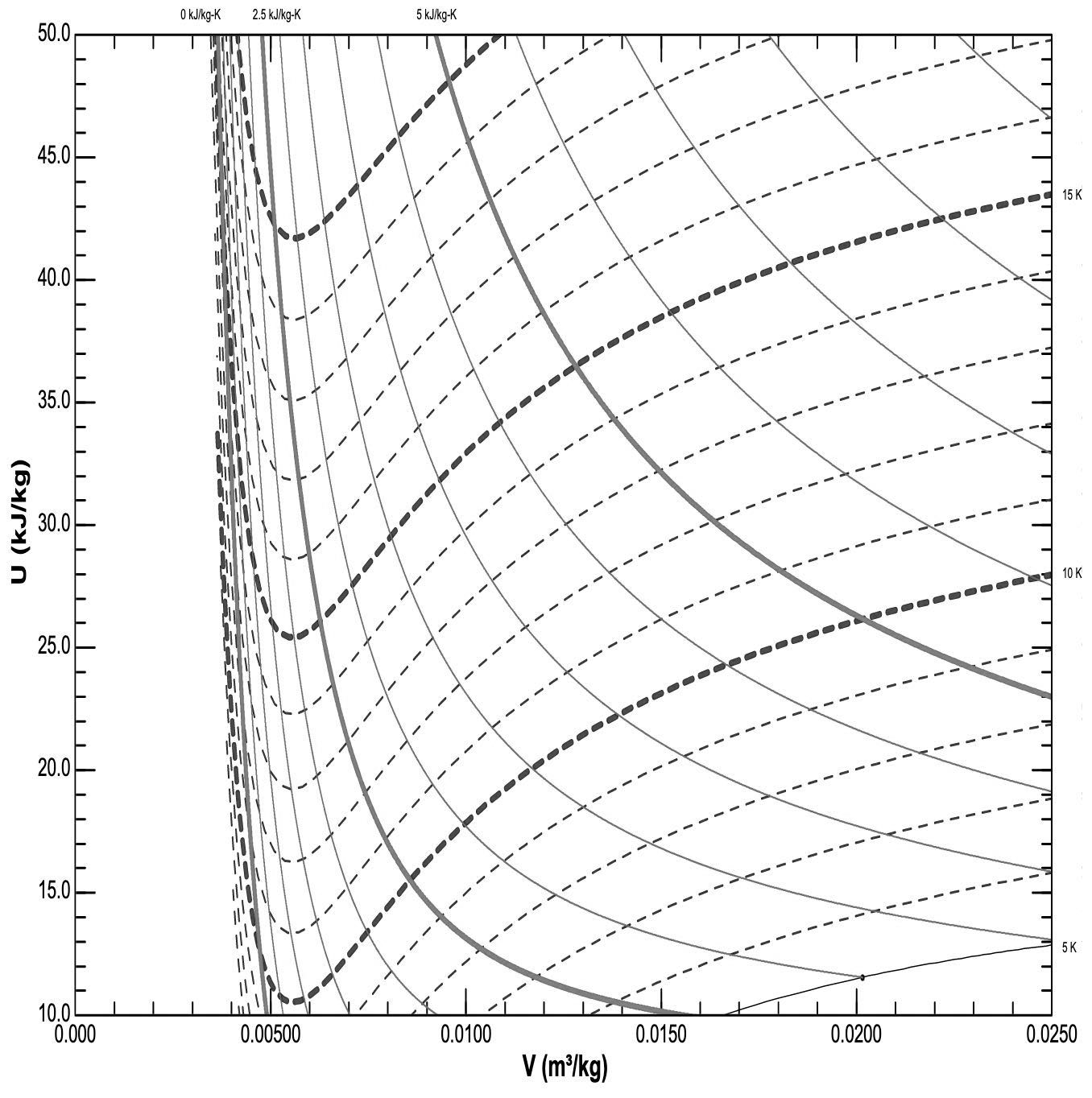
На последнем этапе работы охлаждающей системы гелий из области 1 подается на пористую перегородку, после прохождения которой он оказывается в области 2 и течет к CCD камере для ее охлаждения. Давления и температуры $P_1$, $T_1$ и $P_2$, $T_2$ поддерживаются постоянными.

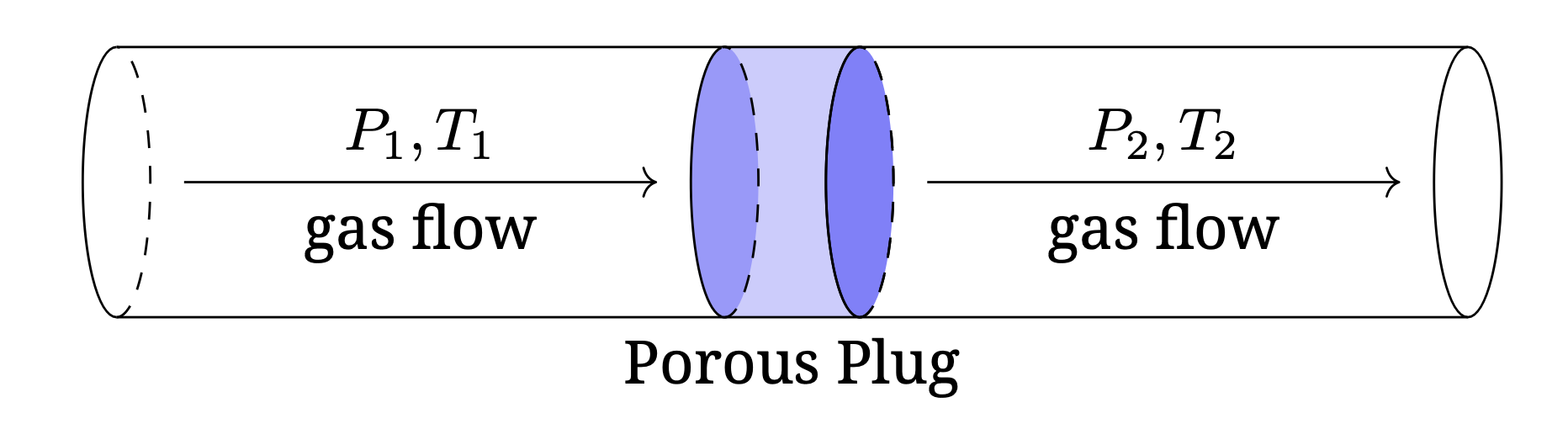
При прохождении пористой перегородки значительную роль играет преодоление сил вязкого трения газа о стенки пор. При этом тепло к газу не подводится и не отводится. Скорость течения газа в области 2 лишь незначительно выше скорости течения газа в области 1.

Гелий в этой задаче нельзя считать идеальным газом, однако он все равно остается газообразным в течение всего процесса.

D1  ^1.00 Пусть 1 моль газа проходит через пористую перегородку.

В листе ответов заполните таблицу, сравнив величины, используя знаки >, <, =, или ? (если без дополнительной информации нельзя сравнить величины).

D2  ^0.60 Через $U$ (внутреннюю энергию), $P$ (давление) и $V$ (объем) выразите величину, которая сохраняется при прохождении 1 моля газа через пористую перегородку. Приведите подтверждающие выкладки.

В листах ответов на графиках зависимости внутренней энергии (на единицу массы) от объема (на единицу массы) построены изотермы и линии постоянной энтропии.

D3  ^1.40 Принимая $V_2 = 0.100\,\mathrm{м^3/кг}$ и $T_2 = 7.5\,\mathrm{K}$ и используя график, рассчитайте численное значение сохраняющейся величины, полученной в пункте D.2. Приведите все необходимые построения на графике.

D4  ^0.80 Найдите максимально возможную $T_1$. Приведите все необходимые построения на графике.

D5  ^0.20 Рассчитайте значение $P_1$, соответствующее полученному вами в пункте D.4 максимальному значению $T_1$.