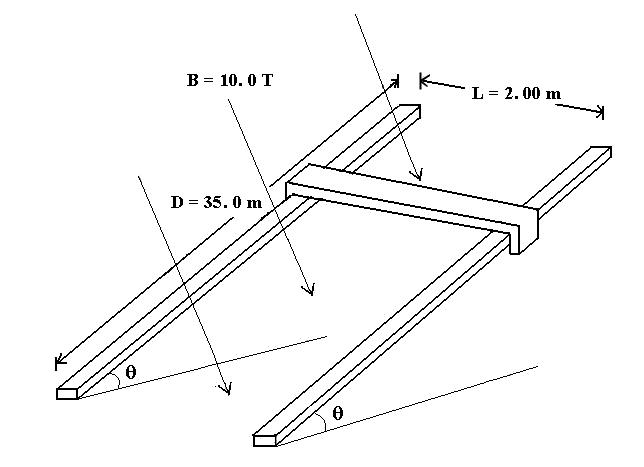
Экспериментатор Глюк находится в точке $P$, в то время как Кузьма Петровна — в точке $Q$. Эти точки разделены проливом шириной 1000 м. После изучения теории рельсотрона экспериментатор Глюк не мог удержаться, чтобы не построить подобное приспособление, чтобы перебросить себя через пролив в точку $Q$. Он сконструировал наклонную плоскость с регулируемым углом наклона $\theta$, на которую положил два параллельных металлических рельса (длина каждого рельса равна $D = 35.0~м$) на расстоянии $L = 2.00~м$ друг от друга. Он подключил источник постоянного тока с напряжением $2424~В$ к концам рельсов. Проводящий стержень может свободно перемещаться по металлическим рельсам так, чтобы экспериментатор Глюк мог безопасно держаться за него во время движения.

Экспериментатор Глюк сконструировал систему, создающую магнитное поле $B = 10.0~Тл$, которое может быть направлено перпендикулярно плоскости рельсов. Масса экспериментатора 70 кг. Масса проводящего стержня 10 кг и его сопротивление $R = 1.0~\Omega$.

Как только он закончил постройку конструкции и проверил, что она правильно работает, ему позвонила Кузьма Петровна и сказала ему прибыть в $Q$ в течение 11 секунд после звонка.

Экспериментатор Глюк сразу же приступил к действиям и запустил себя через пролив в $Q$.

Покажите, используя приведенные ниже пункты, может ли он успеть вовремя и, если да, под каким углом $\theta$ необходимо установить склон?

A1  ^3.00 Выведите выражение для ускорения экспериментатора Глюка вдоль рельсов.

A2  ^1.50 Получите выражение для времени, проведенного на рельсах, $t_s(\theta)$.

A3  ^1.50 Получите выражение для времени, проведенного в полете, $t_f(\theta)$.

A4  ^1.50 Постройте график зависимости полного времени $T = t_s + t_f$ от угла наклона $\theta$.

A5  ^2.50 Учитывая характеристики конструкции, определите диапазон углов наклона, которые ему следует установить.

Примите следующие допущения:
1) Время между концом звонка и всеми приготовлениями (такими как установка нужного угла наклона плоскости) пренебрежимо мало. То есть можно считать, что запуск произошел в момент времени $t = 0$, когда стержень (и экспериментатор Глюк, держащийся за него) начал движение.
2) Экспериментатор Глюк может начать движение с любой точки вдоль металлических рельсов.
3) Более высокий край плоскости и $Q$ находятся на одной высоте, и расстояние между ними равно $w = 1000~м$.
4) Не рассматривайте вопросы безопаcности, например, приземление, электрический шок и т.д.
5) Сопротивление металлических рельсов, внутреннее сопротивление источника тока, трение между проводящим стержнем и рельсами и сопротивление воздуха пренебрежимо малы.
6) Используйте ускорение свободного падения равное $g=10~м/с^2$.

Математические примечания:
1) $\int e^{-a x} dx = -\frac{e^{-ax}}{a} + \text{const}$.
2) Решением уравнения $\frac{dx}{dt} = a + b x$ является
\begin{equation*}
x(t) = \frac{a}{b} \left( e^{b t} - 1 \right) + x(0) e^{b t}.
\end{equation*}