A1  ^0.60 Линейное напряжение между выводами $a$ и $b$ можно представить в виде $\mathcal{E}_{ab} = \mathcal{E'_0} \cos \left(\omega t - \Delta \varphi \right)$, $\mathcal{E'_0} > 0$. Найдите $\mathcal{E'_0}$ и $ \Delta \varphi$. Выразите ответ через $\mathcal{E}_0$.

$$
\mathcal{E}_{ab} = \mathcal{E}_{a} - \mathcal{E}_{b} =\mathcal{E}_{0} \left( \cos \left(\omega t\right) - \cos \left(\omega t - \frac{2\pi}{3}\right)\right).
$$
Применив формулу разности косинусов, получим:
$$
\mathcal{E}_{ab} = 2 \mathcal{E}_{0}\left(\sin\left(\omega t - \frac{\pi}{3}\right) \sin\left(- \frac{\pi}{3}\right)\right) = -\sqrt{3} \mathcal{E}_{0} \sin\left(\omega t - \frac{\pi}{3}\right).
$$
Заменяем синус на требуемый косинус:
$$
\mathcal{E}_{ab} = \sqrt{3} \mathcal{E}_{0}\cos \left(\omega t + \frac{\pi}{6}\right).
$$
$\textit{Примечание.}$
В условии не была указана полярность $\mathcal{E}_{ab}$, поэтому возможен вариант $\mathcal{E}_{ab} = \mathcal{E}_{b} - \mathcal{E}_{a}$. В этом случае знак косинуса в окончательно выражении поменяется, что соответствует сдвигу фазы косинуса на $\pi$:
$$
\mathcal{E}_{ab} = \sqrt{3} \mathcal{E}_{0}\cos \left(\omega t - \frac{ 5\pi}{6}\right).
$$

A2  ^1.00 Пусть каждый из элементов нагрузки ($Z_a$, $Z_b$, $Z_c$) представляет собой последовательно соединенные резистор $R = 9~\text{кОм}$ и конденсатор $C= 2 \cdot 10^{-7}~\text{Ф}$. Найдите амплитуды тока через линейный провод $I_a$ и нулевой провод $I_0$ (формулу и численное значение).

Воспользуемся методом комплексных амплитуд. Будем обозначать комплексные амплитуды чертой над соответствующими величинами. Запишем 2-й закон Кирхгофа для контура с током $I_a$:
$$
\mathcal{E}_{a} = \overline{I_a}(R + r) - \overline{I_a}\frac{i}{\omega C} + \overline{I_0}r\tag{1};
$$
Аналогично для $I_b$, $I_c$:
$$
\mathcal{E}_{b} = \overline{I_a}(R + r) - \overline{I_b}\frac{i}{\omega C} + \overline{I_0}r\tag{2};
$$
$$
\mathcal{E}_{c} = \overline{I_a}(R + r) - \overline{I_c}\frac{i}{\omega C} + \overline{I_0}r\tag{3}.
$$
Также запишем 1-й закон Кирхгофа:
$$
\overline{I_0} = \overline{I_a} + \overline{I_b} + \overline{I_c}\tag{4}.
$$
Выразим $\overline{I_a}$, $\overline{I_b}$, $\overline{I_c}$ из $(1)$, $(2)$, $(3)$ соответственно и подставим в $(4)$:
$$
\overline{I_0} = \frac{\mathcal{E}_{a} - \overline{I_0}r}{R+r - \frac{i}{\omega C}} + \frac{\mathcal{E}_{b} - \overline{I_0}r}{R+r - \frac{i}{\omega C}} + \frac{\mathcal{E}_{c} - \overline{I_0}r}{R+r - \frac{i}{\omega C}}.
$$
Так как
$$
\mathcal{E}_{a}+ \mathcal{E}_{b} +\mathcal{E}_{c} = 0,
$$
получим
$$
\overline{I_0} = 0.
$$
С учетом этого имеем ответ для $\overline{I_a}$:
$$
\overline{I_a} = \frac{\mathcal{E}_{0}}{\left(R + r \right) - \frac{i}{\omega C}},
\\
|\overline{I_a}| = I_a = \frac{\mathcal{E}_{0}}{\sqrt{\left(R + r \right)^2 + \frac{1}{(\omega C)^2}}}.
$$

A3  ^0.40 Найдите коэффициент полезного действия схемы из пункта $\mathrm{A}2$ $\eta$ (формулу и численное значение). Коэффициентом полезного действия считайте отношение средней мощности, выделяющейся на нагрузке, к средней мощности, выделяющейся во всей цепи.

Мощность в схеме выделяется только на резисторах. Полезная мощность выделяется на резисторах $R$. Пусть для этого резистора сдвиг фаз равен $\Delta\varphi_1$. Мощность на резисторе $a$:
$$
P_a = |\overline{I_a}|^2\cos^2(\omega t - \Delta \varphi_1)R = \frac{1}{2}|\overline{I_a}|^2R(1 + \cos(2(\omega t - \Delta \varphi_1)).
$$
Так как среднее $\cos(2(\omega t - \Delta \varphi_1))$ за период равно $0$, средняя за период мощность:
$$
\langle P_a \rangle = \frac{1}{2}|\overline{I_a}|^2R.
$$
Видно, что сдвиг фаз $\Delta \varphi_1$ не влияет на $\langle P_a \rangle$, а значит:
$$
\langle P_a \rangle = \langle P_b \rangle = \langle P_c \rangle.
$$
Итого полезная мощность:
$$
P_{пол} = \frac{3}{2}|\overline{I_a}|^2R.
$$
Аналогично находим общую мощность в цепи:
$$
P_{вся} = \frac{3}{2}|\overline{I_a}|^2(R + r).
$$
По определению, данному в условии:
$$
\eta = \frac{P_{пол}}{P_{вся}} = \frac{R}{R + r} \approx 64{,}3 \text%.
$$

A4  ^1.00 Пусть теперь нагрузка несимметричная: элементы $Z_b$ и $Z_c$ представляют собой резисторы с сопротивлением $R$, а элемент $Z_a$ — конденсатор с емкостью $С_1 = 10^{-9}~\text{Ф}$. Найдите численное значение коэффициента полезного действия схемы $\eta_1$ в этом случае. Получать аналитическое выражение для $\eta_1$ не требуется. Воспользуйтесь численными данными из пункта $A2$.

Модуль импеданса конденсатора:
$$
|Z_a| = \frac{1}{\omega C} = \frac{1}{2\pi f C} \approx 3183кОм.
$$
Заметим, что $|Z_a|\gg R$, поэтому при расчете токов током через конденсатор можно пренебречь. Аналогично пункту $A2$ напишем законы Кирхгофа для цепи:
$$
\overline{I_0} = \overline{I_b} + \overline{I_c}\tag{1};
$$
$$
\mathcal{E}_{0}\left(-\frac{\sqrt{3}}{2}i - \frac{1}{2}\right) = \overline{I_b}(R + r) + \overline{I_0}r\tag{2};
$$
$$
\mathcal{E}_{0}\left(\frac{\sqrt{3}}{2}i - \frac{1}{2}\right) = \overline{I_c}(R + r) + \overline{I_0}r\tag{3}.
$$
Сложим $(2)$ и $(3)$ и воспользуемся $(1)$. Таким образом найдем $\overline{I_0}$:
$$
\overline{I_0} = -\frac{\mathcal{E_0}}{R + 3r}.
$$
Подставив найденное $\overline{I_0}$ в $(2)$ и $(3)$, находим $\overline{I_b}$ и $\overline{I_c}$:
$$
\overline{I_b} = \frac{\mathcal{E_0}}{R + r}\left(-\frac{\sqrt{3}}{2}i + \left(\frac{r}{R + 3r} - \frac{1}{2} \right)\right); I
\\
\overline{I_c} = \frac{\mathcal{E_0}}{R + r}\left(\frac{\sqrt{3}}{2}i + \left(\frac{r}{R + 3r} - \frac{1}{2} \right)\right);
$$
Выражения для модулей:
$$
|\overline{I_0}| = \frac{\mathcal{E_0}}{R + 3r} \approx 12{,}92мА;
\\
|\overline{I_b}|= |\overline{I_с}| = \frac{\mathcal{E_0}}{R + r}\sqrt{\frac{3}{4} + \left(\frac{r}{R + 3r} - \frac{1}{2}\right)^2} \approx 20{,}23мА;
$$
Находим средние полезную и общую мощности:
$$
P_{пол} = 2\frac{1}{2}|\overline{I_b}|^2R;
\\
P_{вся} = 2\frac{1}{2}|\overline{I_b}|^2(R+r) + \frac{1}{2}|\overline{I_0}|^2r;
\\
\eta_1 = \frac{2|\overline{I_b}|^2R}{2|\overline{I_b}|^2(R+r) +|\overline{I_0}|^2r } \approx 59{,}9\text%.
$$

B1  ^0.60 Пусть в одной из квадратных рамок со стороной $a$ в данный момент времени течет ток $I_0$. Найдите магнитное поле $B_0$ в центре квадрата, создаваемое только этой рамкой.

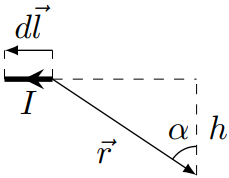
Для одной стороны квадратной рамки $h = a/2$, $\alpha_2 = -\alpha_1 = \pi/4$. Тогда поле в центре рамки:
$$
B_0 = 4\frac{\mu_0 I_0}{4\pi \frac{a}{2}}\left(2\frac{\sqrt{2}}{2}\right) = 2\sqrt{2}\frac{\mu_0I_0}{\pi a}.
$$

B2  ^1.50 Будем теперь рассматривать поле, которое создают все три рамки, токи через которые указаны во введении. Докажите, что в этом случае магнитное поле вращается с постоянной угловой скоростью в плоскости $xy$, то есть его модуль постоянен и равен $B_1$, а угол с осью $x$ $\psi = \omega t + \psi_0$ (тогда $B_x = B_ 1 \cos \psi$, $B_y = B_1 \sin \psi$ ). Найдите $B_1$ и $\psi_0$. Выразите ответ через $B_0$.

Получим проекцию поля от трех рамок на $Ox$:
$$
B_x = B_0\cos(\omega t) + B_0\cos\left(\omega t - \frac{2\pi}{3}\right)\cos\left(\frac{2\pi}{3}\right) + B_0\cos\left(\omega t - \frac{4\pi}{3}\right)\cos\left(\frac{4\pi}{3}\right) =
\\
= B_0\left( \cos(\omega t) - \frac{1}{2}\left(cos\left(\omega t - \frac{2\pi}{3}\right)\ + \cos\left(\omega t - \frac{4\pi}{3}\right)\right)\right).
$$
Применим формулу суммы косинусов:
$$
B_0\left( \cos(\omega t) - \cos\left(\omega t -\pi\right) \cos\left(\frac{\pi}{3}\right)\right) = \frac{3}{2}B_0\cos(\omega t).
$$
Аналогично можно рассчитать проекцию суммарного поля на $Oy$:
$$
B_y = B_0\cos\left(\omega t - \frac{2\pi}{3}\right)\sin\left(\frac{\pi}{3}\right) - B_0\cos\left(\omega t - \frac{4\pi}{3}\right)\sin\left(\frac{\pi}{3}\right),
\\
B_y = \frac{\sqrt{3}}{2}2\sin(\omega t - \pi)\sin\left(-\frac{\pi}{3}\right) = \frac{3}{2}B_0\sin(\omega t).
$$
Оба выражения приводят к ответу:
$$
B_1 = \frac{3}{2}B_0; \qquad \psi_0 = 0.
$$

$\textit{Альтернативное решение.}$
Пусть $\vec{e_x}$, $\vec{e_y}$ — единичные вектора осей $x$, $y$ соответственно.
Запишем с помощью них векторные выражения для полей от трех рамок:
$$
\vec{B_a} = B_0\vec{e_x}\cos(\omega t);
\\
\vec{B_b} = B_0\left(-\frac{1}{2}\vec{e_x} + \frac{\sqrt{3}}{2}\vec{e_y}\right)\cos\left(\omega t - \frac{2\pi}{3}\right);
\\
\vec{B_c} = B_0\left(-\frac{1}{2}\vec{e_x} - \frac{\sqrt{3}}{2}\vec{e_y}\right)\cos\left(\omega t - \frac{4\pi}{3}\right).
$$
Перейдем к комплексным амплитудам:
$$
\vec{B_a} = B_0\vec{e_x}e^{i\omega t};
\\
\vec{B_b} = B_0\left(-\frac{1}{2}\vec{e_x} + \frac{\sqrt{3}}{2}\vec{e_y}\right)e^{i\omega t}e^{-i\frac{2\pi}{3}};
\\
\vec{B_c} = B_0\left(-\frac{1}{2}\vec{e_x} - \frac{\sqrt{3}}{2}\vec{e_y}\right)e^{i\omega t}e^{-i\frac{4\pi}{3}} = B_0\left(-\frac{1}{2}\vec{e_x} - \frac{\sqrt{3}}{2}\vec{e_y}\right)e^{i\omega t}e^{i\frac{2\pi}{3}}.
$$
$$
\vec{B_1} = \vec{B_a}+\vec{B_b}+\vec{B_c} = B_0e^{i \omega t}\left(\vec{e_x}\left(1 - \frac{e^{i\frac{2\pi}{3}}+e^{-i\frac{2\pi}{3}}}{2}\right) - \sqrt{3}i\vec{e_y}\frac{e^{i\frac{2\pi}{3}} - e^{-i\frac{2\pi}{3}}}{2i}\right) =
\\
= B_0e^{i \omega t}\left(\vec{e_x}\left(1 - \cos \left(\frac{2\pi}{3}\right)\right) - \sqrt{3} i\vec{e_y}\sin\left(\frac{2\pi}{3}\right)\right) =
\\
=B_0e^{i \omega t}\left(\frac{3}{2}\vec{e_x} - \frac{3}{2}i\vec{e_y}\right).
$$
Взяв действительную часть от выражения выше, получим:
$$
\vec{B_1} = \frac{3}{2}B_0\left(\vec{e_x}\cos (\omega t) + \vec{e_y}\sin (\omega t)\right).
$$
Отсюда следует полученный ранее ответ.

B3  ^0.40 Маленькая рамка в центре повернута так, что ее нормаль образует угол $\alpha$ с осью $x$. Найдите магнитный поток через нее в момент времени $t$. Выразите ответ через $B_1$, $S$, $\alpha$, $\omega$.

B4  ^1.00 Пусть индуктивность рамки $L_2$, сопротивление $R_2$. Рамка вращается с постоянной угловой скоростью $\omega_1$, так что $\alpha = \omega_1 t$ ($0<\omega_1 < \omega$). В установившемся режиме ток в рамке зависит от времени как
$$
I(t) = A \cos \left( \omega_2 t - \varphi_2\right).
$$
Найдите $A$, $\omega_2$ и $\varphi_2$. Выразите ответ через параметры рамки, $B_1$, $\omega$, $\omega_1$.

Полный поток магнитного поля через рамку создается вращающимся полем и током в рамке $I$
$$
\Phi_t = \Phi + L_2 I
$$
Суммарная ЭДС индукции в рамке с током $I$:
$$
\mathcal{E}= \dot{\Phi}_t = -\dot{\Phi}-L_2\dot{I}.
$$
Из закона Ома для рамки $I R_2 = \mathcal{E}$ получим
$$
-\dot{\Phi} = L_2\dot{I}+IR_2
$$
Это уравнение формально эквивалентно уравнению для $RL$-цепи с источником переменного напряжения $- \dot{\Phi}$.
Будем записывать колебания в комплексном виде:
$$
\Phi = B_1Se^{i (\omega - \omega_1) t}.
$$
Поскольку поток меняется с частотой $\omega_2 = \omega - \omega_1$, с той же частотой будет меняться и ток.
ЭДС индукции в рамке:
$$
\mathcal{E} (t)= -\dot {\Phi} =- i \omega_2B_1Se^{i \omega_2 t}.
$$
Подставим зависимость тока от времени в виде $I = \overline{I} e^{i \omega_2 t}$, получим
$$
(i \omega_2 L_2 + R_2) \overline{I} = - i \omega_2 B_1 S;
$$
$$
\overline{I} = -\frac{i(\omega - \omega_1)B_1S}{i(\omega - \omega_1)L_2 + R_2}.
$$
Отсюда получаем ответы
$$
\omega_2 = \omega - \omega_1
\\
A = |\overline{I}| = \frac{B_1S(\omega - \omega_1)}{\sqrt{R_2^2 + (\omega - \omega_1)^2L_2^2}} ;
\\
\varphi_2 =\pi- \arctan\left(\frac{R_2}{(\omega - \omega_1) L_2}\right).
$$

B5  ^1.50 Для того, чтобы обеспечить более равномерное вращение ротора, вместо одной рамки будем использовать три рамки, повернутых друг относительно друга на $120^\circ$ вокруг оси $z$ (то есть если положение одной рамки задается углом $\alpha$, положения остальных рамок задаются углами $\alpha_2 = \alpha + 2\pi/3$, $\alpha_3 = \alpha + 4\pi/3$). Рамки изолированы друг от друга, их взаимной индукцией можно пренебречь. Докажите, что проекция на ось $z$ момент сил, действующий на конструкцию из трех рамок, постоянен. Найдите ее величину $M_z$. Выразите ответ через параметры рамки, $B_1$, $\omega$, $\omega_1$.

Магнитный поток вращающегося магнитного поля через $i$-ю рамку ($i = 1,\, 2,\, 3$) равен $\Phi_i = B_1 S \cos (\omega_2 t - \alpha_{0i})$ ($\alpha _{01} = 0$, $\alpha_{02} = 2\pi/3 = \Delta \alpha$, $\alpha_{03} = 4\pi/3 = 2 \Delta \alpha$). Таким образом, магнитный поток через вторую и третью рамку запаздывают на $2\pi/3$ и $4 \pi/3$. Тогда токи через эти рамки запаздывают на такую же фазу.
Магнитный момент рамки с током $I$ площадью $S$
$$
m = IS,
$$
на $i$-тую рамку действует момент сил
$$
\vec {M_i} = [\vec{m_i} \times \vec {B}].
$$
В проекции на $Oz$:
$$
M_{iz} = m_iB_1\sin(\psi - \alpha_i).
$$
Таким образом (обозначения для тока взяты из предыдущего пункта):
$$
M_z =B_1AS(\sin(\omega_2 t)\cos(\omega_2 t - \varphi_2) + \sin(\omega_2 t-\Delta\alpha)\cos(\omega_2 t - \varphi_2-\Delta\alpha) +
\\
+ \sin(\omega_2 t-2\Delta\alpha)\cos(\omega_2 t - \varphi_2 - 2\Delta\alpha)).
$$
Применим формулу произведения синуса на косинус:
$$
M_z = \frac{1}{2}B_1AS\left(\sin \varphi_2 + \sin(2\omega_2 t - \varphi_2)+\sin \varphi_2 + \sin(2\omega_2 t - \varphi_2 - 2\Delta\alpha) )+\\
+ \sin \varphi_2 + \sin(2\omega_2 t - \varphi_2 - 4\Delta\alpha \right) $$
Сумма трех синусов, зависящих от времени, обращается в 0, поэтому
$$
M_z= \frac{3}{2}B_1AS\sin \varphi_2.
$$
Подставив $\varphi_2$, $A$, получим
$$
\sin \varphi_2 = \sin \left( \arctan \frac{R_2}{(\omega - \omega_1)L_2}\right) = \frac{R_2}{\sqrt{R_2^2 + (\omega- \omega_1)^2 R_2^2}}.
$$

$\textit{Альтернативное решение.}$
Найдем суммарный момент трех рамок с током. Эта задача математически эквивалентна задаче о нахождении суммарного магнитного поля от трех внешних рамок с током. Действительно, магнитный момент каждой следующей рамки повернут на $120^\circ$ градусов относительно магнитного момента предыдущей рамки, и запаздывает по фазе на $2\pi/3$. Рассмотрим сначала задачу в системе отсчета вращающихся рамок. Тогда если $m_0 = AS$ — амплитуда магнитного момента от одной рамки, то величина суммарного магнитного момента $m_1 = \dfrac{3}{2} m_0$, а магнитный момент вращается с угловой скоростью $\omega_2$. При этом начальная фаза магнитного момента равна $- \varphi_2$, поскольку все токи запаздывают относительно магнитного поля на эту фазу. Поскольку сами рамки вращаются с угловой скоростью $\omega_1$, относительно лабораторной системы отсчета магнитный момент вращается с угловой скоростью $\omega_1 + \omega_2 = \omega$. Угловые скорости магнитного момента и магнитного поля совпадают, поэтому угол между ними остается постоянным. Отсюда следует, что момент сил также постоянен и равен
$$
M_z = \frac{3}{2} m_0 B_1 \sin \varphi_2 =\frac{3}{2} AS B_1 \sin \varphi_2.
$$
Таким образом, получаем прежний ответ.

B6  ^1.00 Постройте качественный график зависимости $M _z(\omega_1)$ в диапазоне частот $0 < \omega_1 < \omega$. Укажите координаты характерных точек. Считайте, что $R_2/L_2 < \omega$.

Перепишем выражение для момента сил в виде
$$
M = \frac{3}{2}B_1^2S^2\frac{R_2}{L_2^2}\frac{1}{(\omega - \omega_1)+ \frac{R_2^2}{L_2^2}\frac{1}{(\omega - \omega_1)}}.
$$
Максимуму момента отвечает минимум знаменателя
$$
(\omega - \omega_1)+ \frac{R_2^2}{L_2^2}\frac{1}{(\omega - \omega_1)}.
$$
Взяв производную по $\omega - \omega_1$, получим, что экстремуму соответствует
$$
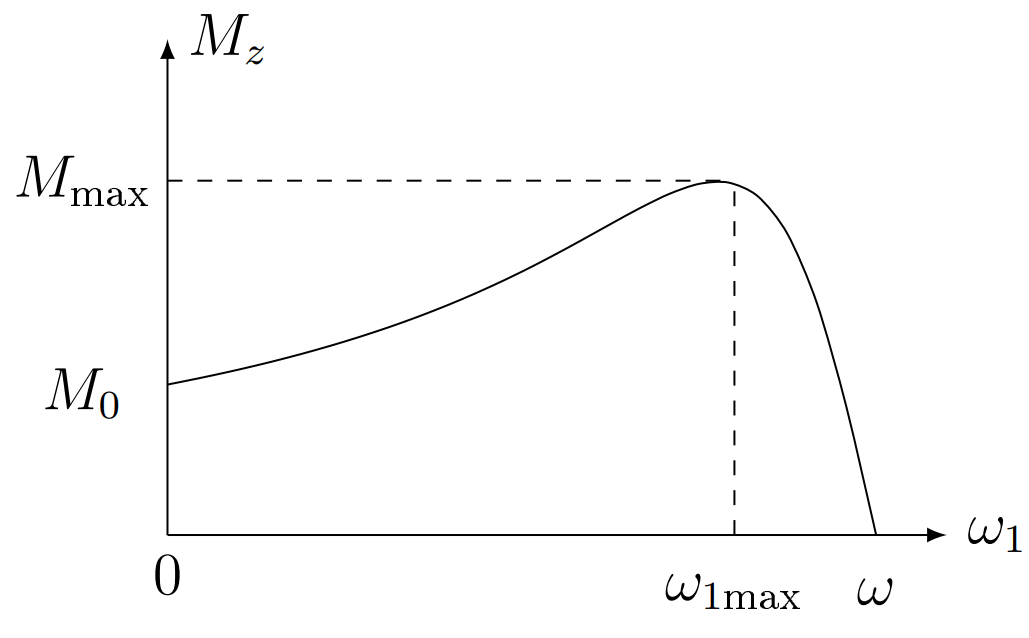
\omega - \omega_{1max} = \frac{R_2}{L_2};
\\
\omega_{1max} = \omega - \frac{R_2}{L_2}.
$$
Максимальное значение момента $M_{max} = \frac{3}{4}\frac{B_1^2 S^2}{L_2}$. Любопытно отметить, что $M_{max}$ не зависит от $R_2$.
При $\omega_1$ = 0
$$
M_0 = \frac{3}{2}B_1^2S^2\frac{\omega R_2}{\omega^2L_2^2 + R_2^2}.
$$