Pho.rs: Электрическая дуга

A1 ^1.00 Запишите условия механического равновесия для плазменного шнура и найдите зависимость давления от радиальной координаты $p(r)$.

A1. 1 Зависимость $B(r)=\mu_0 jr/2$	0.30
A1. 2 Условие равновесия $jB(r)+\mathrm dp{/}\mathrm dr=0$	0.30
A1. 3 Зависимость $p(r)=\frac{\mu_0j^2}4(C-r^2)$	0.20
A1. 4 Граничные условия $p(R)=0$	0.20

A2 ^0.50 Считая, что на границе шнура давление пренебрежимо мало, получите зависимость радиуса шнура от напряжения, пользуясь соотношением $j=\lambda E$, где $E$ – напряженность поля, $\lambda$ – проводимость среды (считайте её постоянной). Соотношение выше – это закон Ома, записанный в дифференциальной форме

A2. 1 Зависимость $r(j)=\sqrt{4nk_\mathrm BT/\mu_0j^2}$	0.10
A2. 2 Зависимость $r(U)=\frac{2d}{\lambda(U-U_0)}\sqrt{\frac{nk_\mathrm BT}{\mu_0}}$	0.40

A3 ^0.50 Покажите, что из результатов пунктов A1 и A2 следует схожий вид зависимости. Найдите значения $a$ и $b$ через заданные параметры дуги и физические постоянные.

A3. 1 Зависимость приведена к виду $U=U_0+\frac{4\pi dnk_\mathrm BT}{\mu_0\lambda}I^{-1}$	0.10
A3. 2 Найдено $a=U_0$	0.20
A3. 3 Найдено $b=\frac{4\pi dnk_\mathrm BT}{\mu_0\lambda}$	0.20

B1 ^1.00 Постройте вольтамперные характеристики для всей цепи (кроме источника) для каждого из случаев. Укажите на графике точки, в которых может возникнуть разряд.

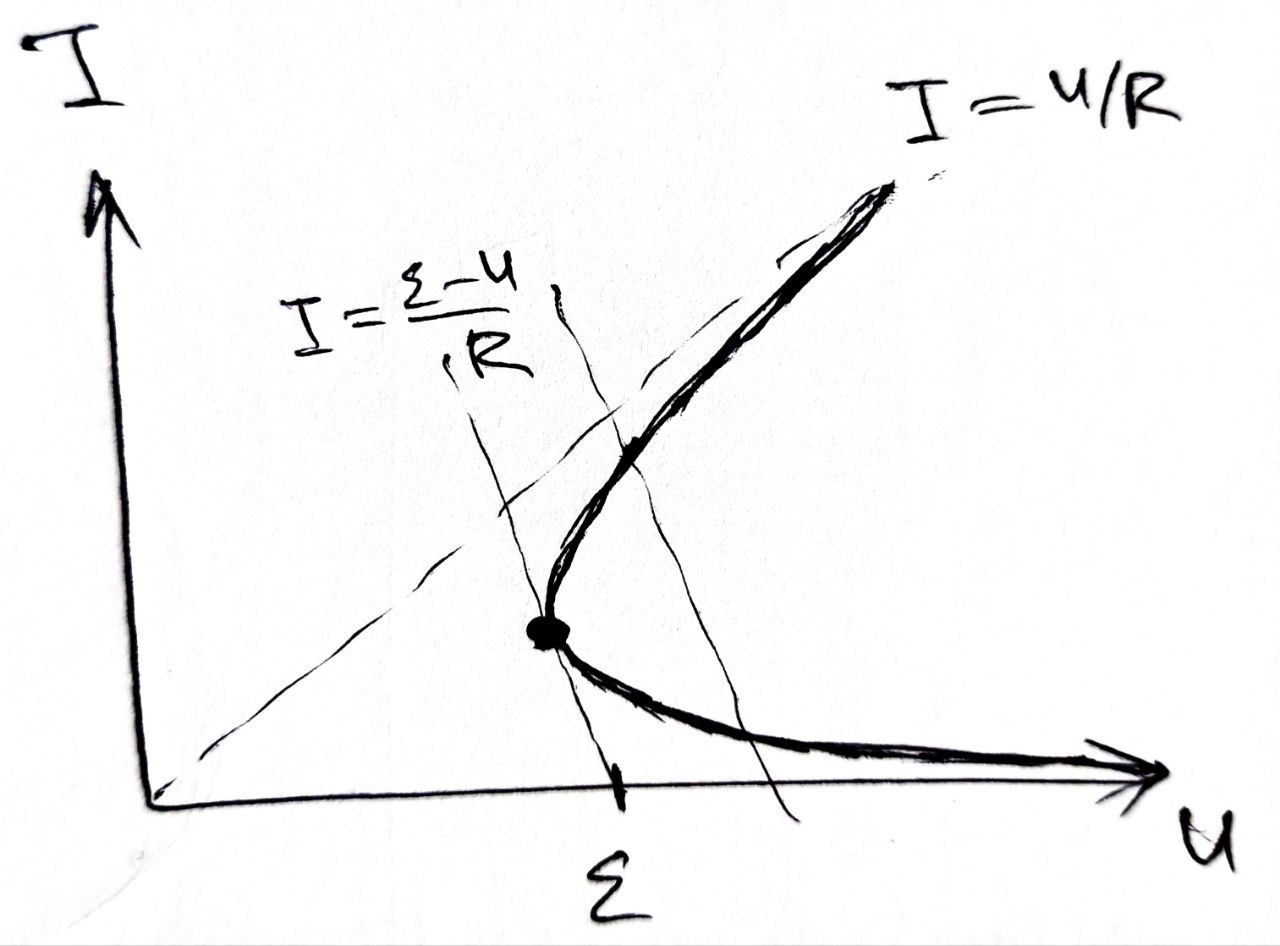
B1. 1 ВАХ последовательного соединения	0.50
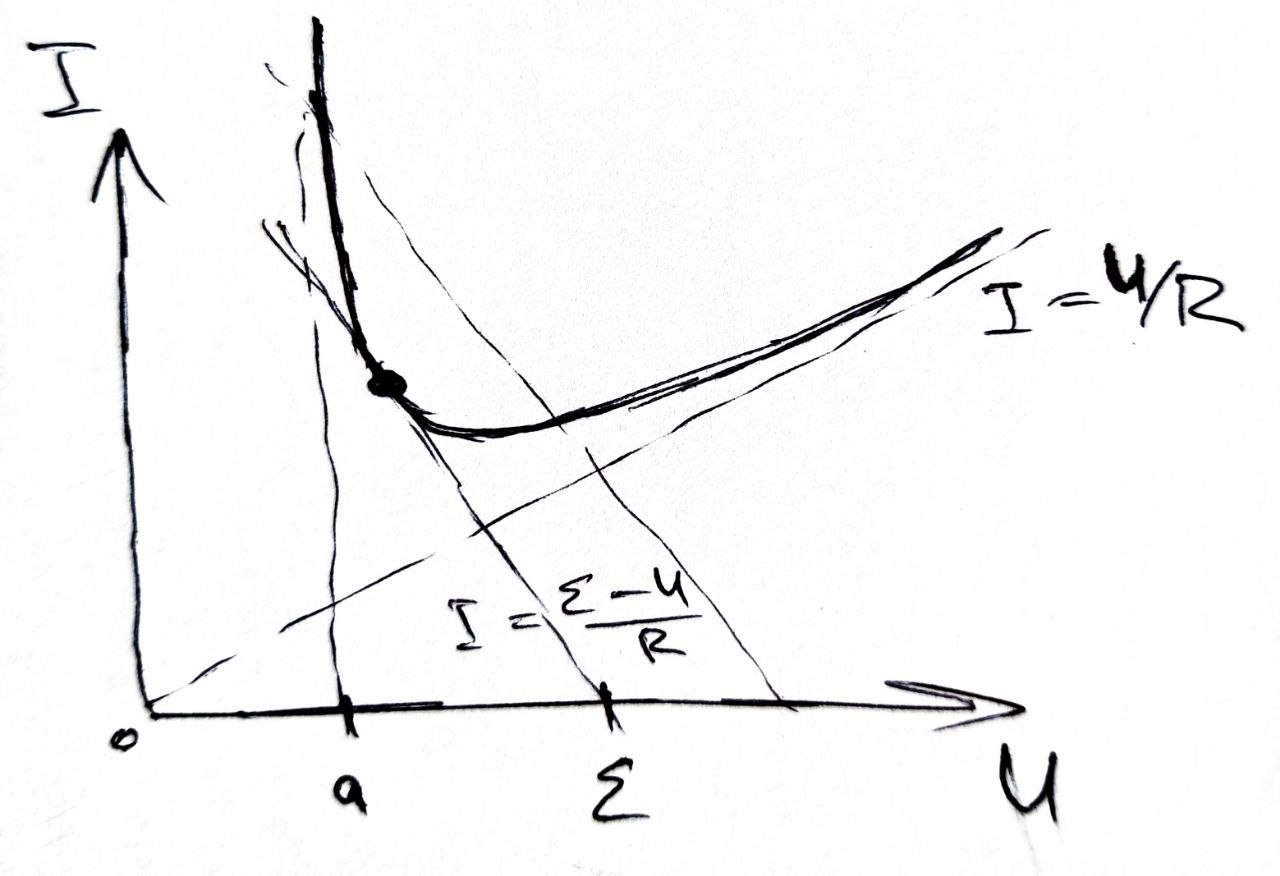
B1. 2 ВАХ параллельного соединения	0.50

B2 ^2.00 С помощью схем, графиков, формул проанализируйте возможности получения устойчивого разряда. Укажите все точки, где получается устойчивый и неустойчивый разряд.

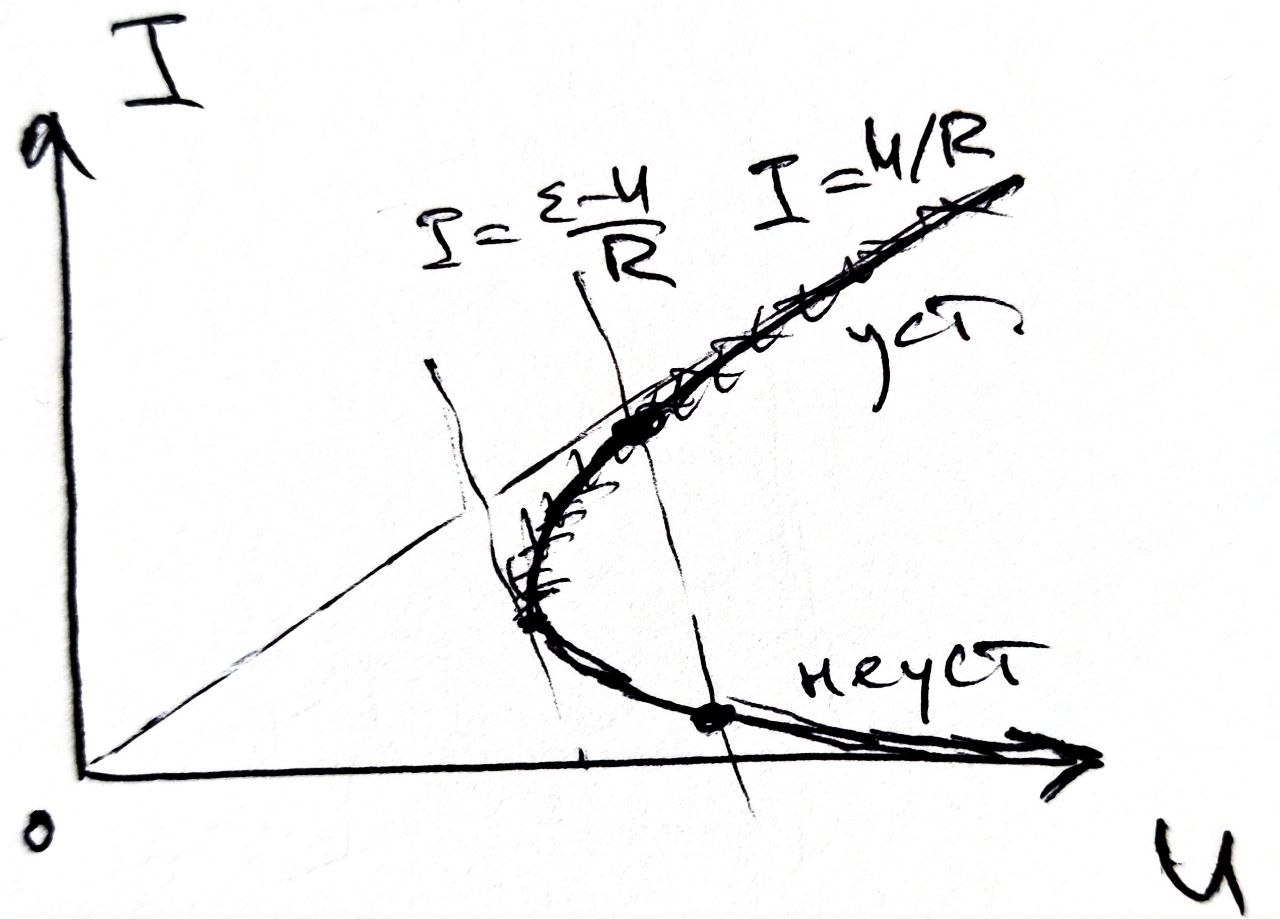
B2. 1 Схема с указанием возможных точек	0.50
B2. 2 Обоснована неустойчивость первой точки	0.75
B2. 3 Обоснована устойчивость второй точки	0.75

B3 ^0.50 Найдите значения тока в разряде (т.н. рабочие точки) через $\mathcal{E}$, $R$, $r$, $a$, $b$.

B3. 1 Найдены оба значения силы тока $I_{1,2}=\frac{\mathcal E\pm\sqrt{\mathcal E^2-4b(R+r)}}{2(R+r)}$

0.50

B4 ^1.50 Найдите условие устойчивости тока разряда. Ответ выразите через $R$, $r$ и $b$.

B4. 1 Указано, что дифференциальное сопротивление отрицательно	0.50
B4. 2 Получено соотношение $I>\sqrt\frac{b}{R+r}$	1.00

B5 ^0.50 Найдите максимальное значение сопротивления $R$, для которого можно получить стационарный разряд для заданного источника $\left(\mathcal{E}{,}r\right)$.

B5. 1 Ответ для $R_{max}=\frac{(\mathcal E-a)^2}{4b}-r$

0.50

B6 ^1.00 Нарисуйте на одном графике зависимость выделяемой мощности от силы тока $P=f(I)$ для каждого элемента цепи и для всей цепи в целом. Отметьте на графике точки, в которых возможно горение дуги.

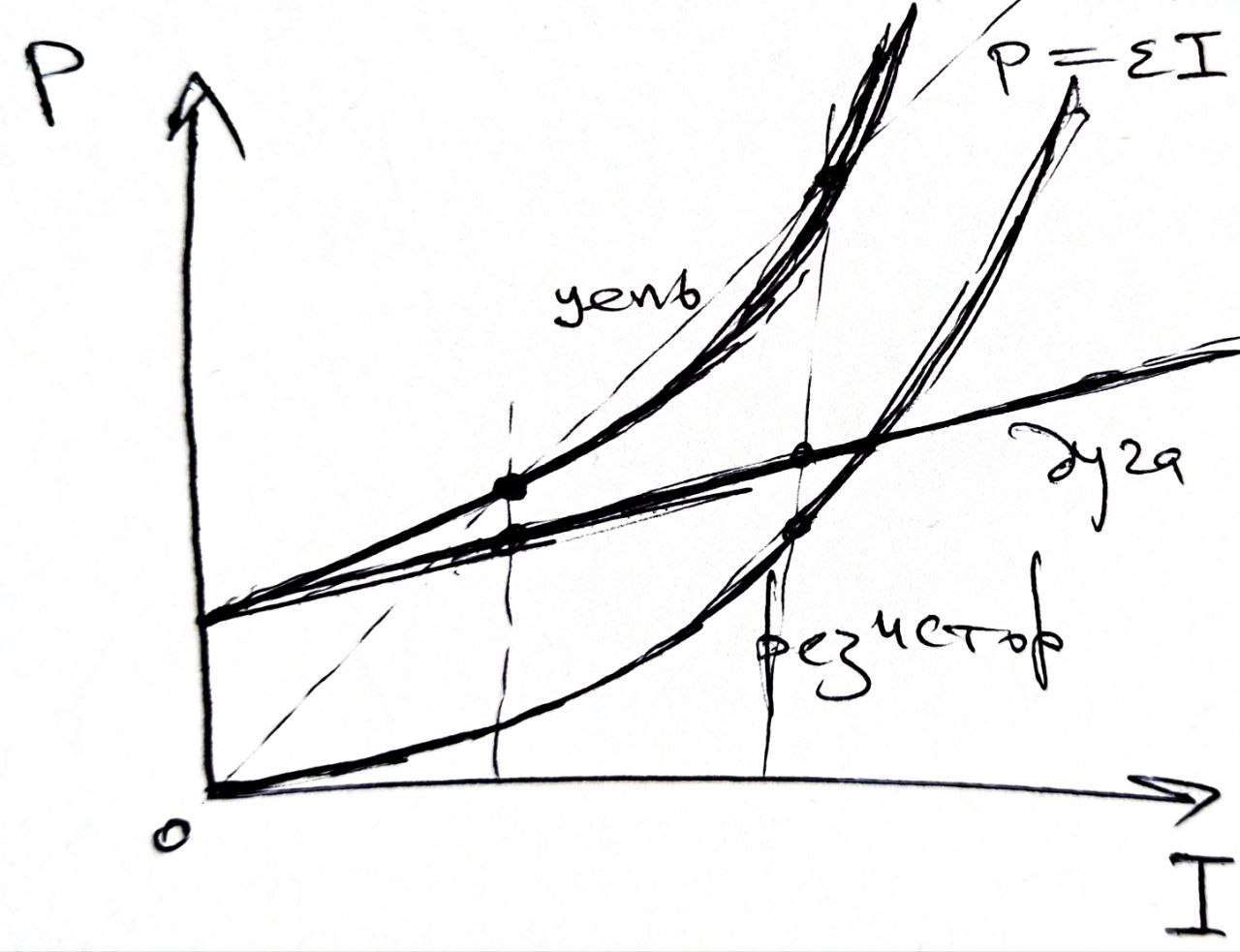
B6. 1 Построены графики (по 0.25 за каждый).	3 × 0.25
B6. 2 Указаны точки	0.25

C1 ^1.00 Определите вид зависимости коэффициентов $a$ и $b$ от длины дуги и численные значения характерных параметров.

C1. 1 Линейность	0.40
C1. 2 Коэффициенты линейной зависимости	2 × 0.20
C1. 3 Значение $	0.20

C2 ^0.50

С дугой, исследуемой в пункте C1, проводится следующий эксперимент. После получения устойчивого разряда длина дугового промежутка начинает увеличиваться, при этом ЭДС в цепи изменяется так, чтобы поддерживать ток через дугу постоянным и равным $I=5~\text{А}$. Полное омическое сопротивление цепи (без дуги) равно $R=2~\text{Ом}$. Определите:

при какой длине дуги разряд станет нестационарным;
какова при этом будет ЭДС источника.

C2. 1 Выражение для минимальной стабильной силы тока $$	0.10
C2. 2 Найдена максимальная длина (формула + число)	2 × 0.10
C2. 3 Найдена ЭДС (формула + число).	2 × 0.10

Электрическая дуга

Разбалловка