Pho.rs: Диэлектрический полуцилиндр

1 ^12.00 Найдите распределение напряжённости электрического поля $E(\varphi)$ и его потенциала $V(\varphi)$ в среде.

Ответ: При $0 \leq \varphi < \theta_0$:

$$E_1=\frac{V_0}{\left[ \theta_0 + \frac{\sigma_1}{\sigma_2} \left( \pi - \theta_0 \right) \right] r},\ V_{\varphi}=\frac{\left( \theta_0 - \varphi \right) + \frac{\sigma_1}{\sigma_2} \left( \pi - \theta_0 \right)}{\theta_0 + \frac{\sigma_1}{\sigma_2} \left( \pi - \theta_0 \right)};$$

при $\theta_0 < \varphi \leq \pi$:

$$E_2=\frac{V_0}{\left[ \frac{\sigma_2}{\sigma_1} \theta_0 + \left( \pi - \theta_0 \right) \right] r},\ V_{\varphi}=\frac{\pi - \varphi}{\frac{\sigma_2}{\sigma_1} \theta_0 + \left( \pi - \theta_0 \right)}.$$

2 ^4.00 Найдите полный заряд $Q$ на границе между диэлектриками (т.е. при $\varphi=\theta_0$).

Ответ: $$Q=\frac{\varepsilon_0 \left( \frac{\sigma_1}{\sigma_2} - 1 \right) l \ln{\frac{b}{a}}}{\left[ \theta_0 + \frac{\sigma_1}{\sigma_2} \left( \pi - \theta_0 \right) \right]}V_0.$$

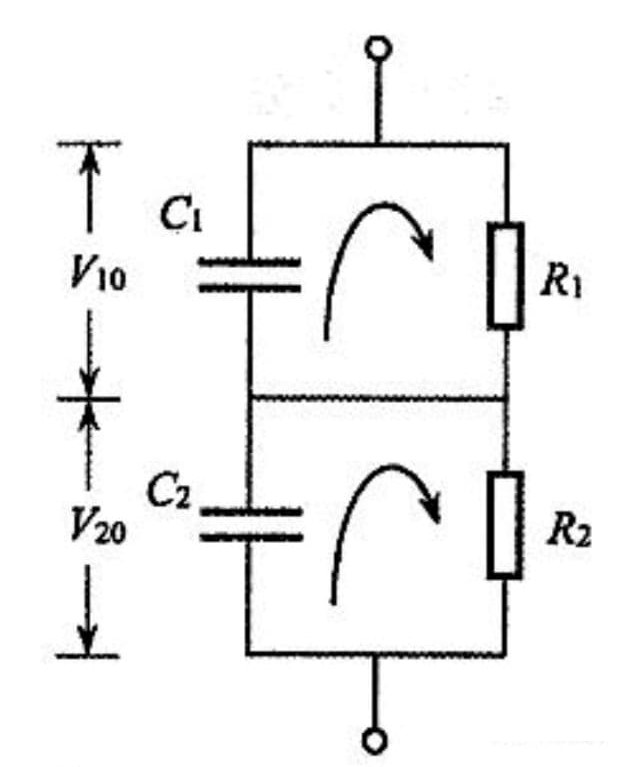
3 ^12.00 Найдите сопротивление и ёмкость $R_1$, $C_1$ и $R_2$, $C_2$ каждого из диэлектриков (т.е. областей $0 \leq \varphi < \theta_0$ и $\theta_0 < \varphi \leq \pi$ соответственно).

Ответ: $$R_1=\frac{\theta_0}{\sigma_1 l \ln{\frac{b}{a}}},\ C_1=\frac{\varepsilon_{r1} \varepsilon_0 l}{\theta_0} \ln{\frac{b}{a}},\\R_2=\frac{\left( \pi - \theta_0 \right)}{\sigma_2 l \ln{\frac{b}{a}}},\ C_2=\frac{\varepsilon_{r2} \varepsilon_0 l}{\left( \pi - \theta_0 \right)} \ln{\frac{b}{a}}.$$

4 ^8.00 В момент времени $t=0$ напряжение выключают. Считая дальнейшие процессы квазистатическими, найдите зависимость напряжения между нижними поверхностями полуцилиндра $V(t)$ от времени и нарисуйте эквивалентную схему процесса.

Ответ: $$V(t)=\frac{\theta_0 V_0}{\left[ \theta_0 + \frac{\sigma_1}{\sigma_2} \left( \pi - \theta_0 \right) \right]}e^{-\frac{\sigma_1}{\varepsilon_{r1} \varepsilon_0}t}+\frac{\left( \pi - \theta_0 \right) V_0}{\left[ \frac{\sigma_2}{\sigma_1} \theta_0 + \left( \pi - \theta_0 \right) \right]}e^{-\frac{\sigma_2}{\varepsilon_{r2} \varepsilon_0}t}.$$

Диэлектрический полуцилиндр

Решение