Данное задание разработано на материалах обзорной статьи: Synergy of physical properties of low-dimensional carbon-based systems for nanoscale device design/ N. A. Poklonski, S.A. Vyrko, A. I. Siahlo, O. N. Poklonskaya, S. V. Ratkevic, N. N. Hieu, A. A. Kocherzhenko/ Matter. Res. Express, 6 (2019).

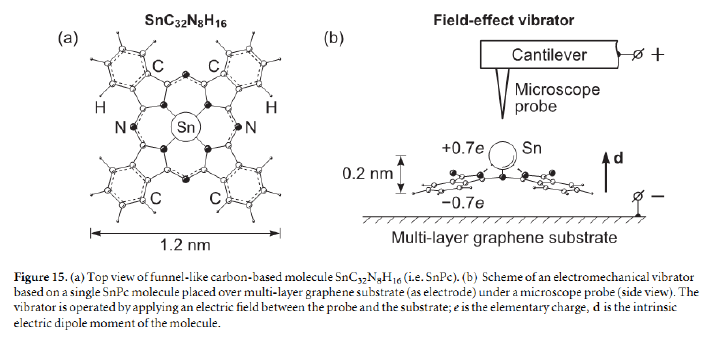
На рисунке, взятом из указанной статьи, показана схема вибратора, управляемого электрическим полем. Сложная плоская молекула (показанная на рисунке слева) содержит атом олова ($\mathrm{Sn}$). Этот атом может колебаться в направлении, перпендикулярном плоскости
молекулы. Частота этих колебаний может изменяться под действием электрического поля. Строгий расчет характеристик молекулярных колебаний возможен только с помощью квантовой механики.

Однако наиболее характерные особенности движения этого атома могут быть получены и в рамках классической физики. Для этого рассмотрим следующую упрощенную модель рассмотренного вибратора.

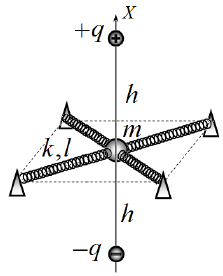
При выполнении данного задания рекомендуем использовать приближенную формулу
$$
(1+z)^\gamma=1+\gamma z+\frac{\gamma(\gamma-1)}{2 !} z^2+\frac{\gamma(\gamma-1)(\gamma-2)}{3 !} z^3+\ldots
$$
Эта формула справедлива для малых значений безразмерной величины $z\ll 1$ и любого показателя степени $\gamma$. Каждый раз при использовании этой формулы подумайте, сколько слагаемых следует оставлять для дальнейших преобразований.

Часть 1. Силы упругости

1.1  ^0.60 Найдите зависимость суммарной силы упругости $F(x)$, действующей на шарик со стороны 4 пружин, от смещения шарика $x$.

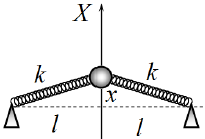
Напоминаем, что, когда шарик находится в центре квадрата, пружины не деформированы!

1.2  ^0.40 Покажите, что при $x\ll l$ формулу для суммарной силы упругости можно приближенно представить в виде
$$F=Cx^n.$$
Найдите значения постоянных величин $C$ и $n$ в этой формуле.

1.3 Укажите, будут ли колебания шарика при отсутствии электрического поля гармоническими?

Часть 2. Электрическое поле и электрические силы

2.1  ^1.00 Найдите зависимость модуля напряженности электрического поля $E(x)$ на оси $X$ от координаты $x$. Постройте схематический график этой зависимости.

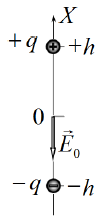
В дальнейшем вместо координаты шарика x используйте безразмерную величину $z=x/h$. При малых значениях $x\ll h$, полученную зависимость $E(x)$ с помощью приближенной формулы, приведенной выше, можно представить в виде
$$E(z)=E_0(1+a_1 z+ a_x z^2 + \dots),$$
где $E_0$ — напряженность поля в начале координат $a_1$, $a_2$, $a_3$, $\dots$ численные коэффициенты. В этой формуле следует оставить столько слагаемых, сколько потребуется для дальнейших расчетов.

2.2  ^1.00 Выразите значение $E_0$ через значения $q$, $h$. Рассчитайте значения коэффициентов $a_1$, $a_2$, $a_3$, $\dots$

В дальнейшем считайте величину $E_0$ известной. В дальнейших расчетах используйте только приближенную формулу выше с найденными численными коэффициентами.
Под действием электрического поля напряженности $E$ шарик поляризуется и приобретает дипольный момент, модуль которого равен
$$p=\alpha\varepsilon_0 E,$$
где $\alpha$ — поляризуемость шарика (считайте ее известной), $\varepsilon_0$ — электрическая постоянная.
Со стороны электрического поля на электрический диполь действует сила
$$F=p\frac{dE}{dx}.$$

2.3  ^0.50 Найдите зависимость силы $G(z)$, действующей на шарик со стороны электрического поля, от положения шарика $z$.

2.4  ^2.00 Представьте полученную зависимость в приближенной виде
$$G(z)=G_1\cdot(b_0 + b_1 z + b_2 z^2 + \dots),$$
где $G_1$ — значение функции $G(z)$ при $z=1$. Выразите значение $G_1$ через величины $E_0$, $\alpha$ и $h$. Найдите численные значения коэффициентов $b_0$, $b_1$, $b_2$, $\dots$. Оставьте в этой формуле столько слагаемых, сколько необходимо для дальнейших расчетов.

Часть 3. Колебания шарика

3.1  ^0.50 Представьте зависимость силы упругости от положения шарика в виде
$$F(z)=F_1\cdot z^n,$$
где $F_1$ — значение функции при $z=1$. Выразите значение $F_1$ через заданные параметры модельной системы.

При включении электрического поля положение равновесия шарика смещается. Обозначим координату положения равновесия $z_0$.

3.2  ^1.00 Выразите значения координаты положения равновесия $z_0$ через параметры системы $F_1$ и $G_1$.

3.3  ^0.50 Найдите максимальное значение напряженности электрического поля в начале координат $E_{0\max}$, при котором шарик может совершать колебания.

3.4  ^2.00 Рассчитайте частоту $\nu$ малых колебаний шарика вблизи положения равновесия $z_0$, если напряженность электрического поле в начале координат $E_0 < E_{0\max}$. Выразите значения частоты $\nu$ через параметры $F_1$, $G_1$, $z_0$ и $m$.