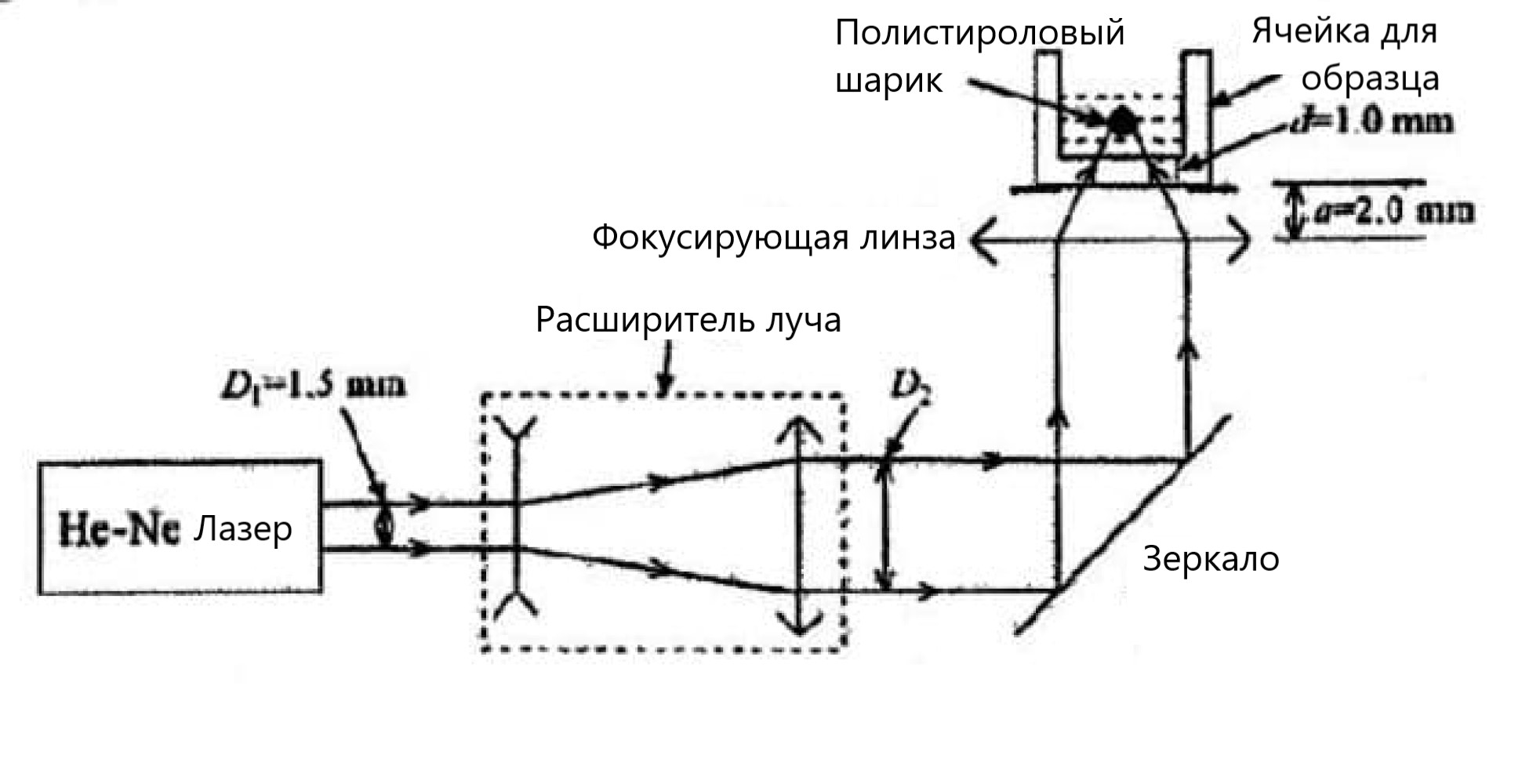
Часть Нобелевской премии 2018 года по физике была присуждена американскому учёному Артуру Эшкину за инновационную работу в создании оптических ловушек (т.н. оптического пинцета). Оптический пинцет использует сфокусированные лазерные лучи для захвата крошечных предметов. На рисунке (a) схематически показана экспериментальная установка для оптического пинцета. Частота гелий-неонового лазера равна $\lambda=632.8~\text{нм}$, диаметр лазерного луча $D_1=1.5~\text{мм}$, его мощность $P=30~\text{мВ}$. Чтобы улучшить захватывающую способность, можно добавить расширитель луча. После отражения от зеркала лазерный луч попадает на собирающую линзу с фокусным расстоянием $F=4~\text{мм}$, и фокусируется в слое дистиллированной воды в ячейке для образца. Некоторое количество полистироловых шариков добавлено в воду в ячейке. Диаметр шариков $D_b=2.0~\text{мкм}$, их плотность $\rho_b=1.0\cdot10^3~\frac{\text{кг}}{\text{м}^3}$, коэффициент преломления стекла, из которого сделана стенка ячейки, $n_g=1.46$, коэффициент преломления воды в ячейке $n_w=1.33$, толщина стеклянной стенки ячейки $d=1.00~\text{мм}$, расстояние между внешним краем стенки и поверхностью фокусирующей линзы $a=2.00~\text{мм}$, температура воды $T=300~\text{К}$, показатель преломления воздуха $n_0=1.00$, ускорение свободного падения $g=9.80~\frac{\text{м}}{\text{с}^2}$, константа Больцмана $k_B=1.38\cdot10^{-23}~\frac{\text{Дж}}{\text{К}}$. Шарики могут быть захвачены пинцетом при прохождении точки фокусировки лазерного луча.

1  ^4.00 Найдите диаметр светового пятна $D_{o1}$, которое образует луч в фокальной плоскости в воздухе в отсутствие расширителя луча.

2  ^4.00 Чтобы улучшить захватывающую способность оптического пинцета, используют расширитель луча. Как показано на рисунке (a), расширитель луча состоит из рассеивающей линзы с фокусным расстоянием $f_1=-6.3~\text{мм}$ и собирающей линзы с фокусным расстоянием $f_2=25.2~\text{мм}$. Считая, что расширяемый пучок состоит из параллельных лучей, найдите расстояние между линзами $l$ и диаметр расширенного пучка $D_2$.

3  ^8.00 Расширенный пучок фокусируется в слое дистиллированной воды в ячейке для образца, как показано на рисунке (a). В параксиальном приближении найдите, на каком расстоянии $D_w$ от внутренней поверхности ячейки сфокусируется пучок и какого диаметра $D_{o2}$ пятно он образует в фокальной плоскости.

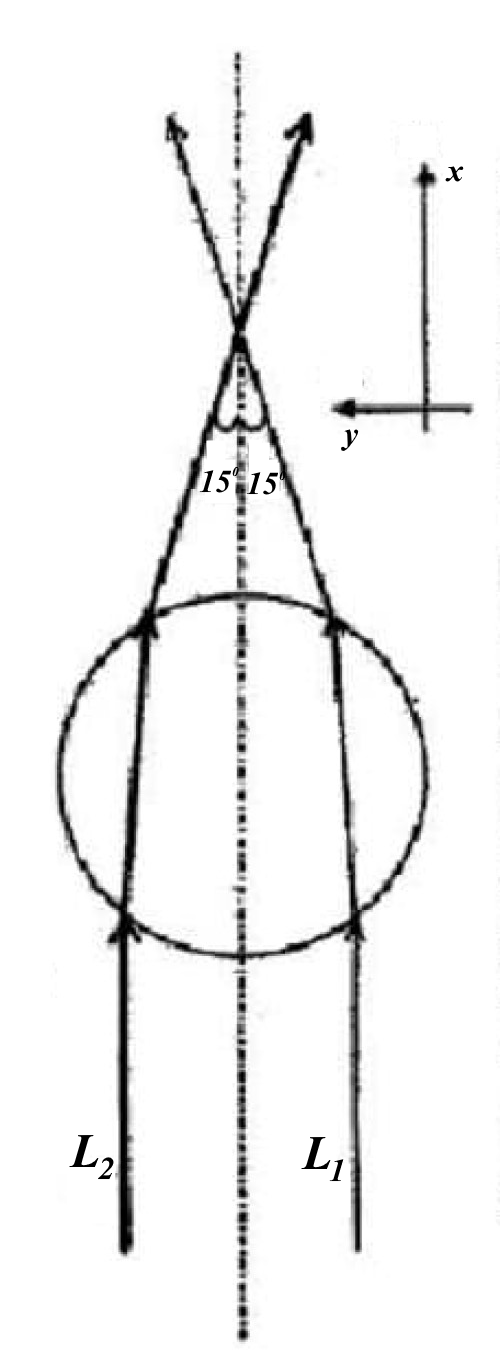
4  ^12.00 На рисунке (b) показана модель поведения погружённых в воду полистироловых шариков под действием неоднородного лазерного пучка (упрощённо представленного в виде двух лучей с разной интенсивностью). Лучи $L_1$ и $L_2$ падают вдоль оси $Ox$ и имеют мощности $P_1=1.0~\text{мВ}$ и $P_2=2.0~\text{мВ}$ соответственно. Угол, на который отклоняются лучи вследствие преломления, равен $15^{\circ}$, как показано на рисунке (b). Отражением от границы раздела сред и поглощением света пренебрегите. Найдите силу $\vec{F_b}$, действующую на шарик со стороны лучей, выразив её через единичные векторы $\vec{i}$ и $\vec{j}$ вдоль $Ox$ и $Oy$ соответственно и отношения $\eta_x$ и $\eta_y$ проекций силы на эти оси к силе притяжения, действующей на шарик.

5  ^4.00 Найдите среднеквадратическую скорость шариков $v_p$, находящихся в воде при температуре $300~\text{К}$.

6  ^4.00 При рассмотрении оптических пинцетов можно также рассматривать модель оптического потенциального колодца, и потенциал $U(r)$ сферически симметричного колодца, создаваемого сфокусированным на шарике лазерным лучом, может быть описан как$$\begin{cases}U_0\left(1-\frac{r^2}{b^2}\right),\ \text{если}\ r\leq b;\\0,\ \text{если}\ r>b;\end{cases}$$где $b$ — некоторая константа, $r$ — расстояние от центра колодца, а $U_0=0.078~\text{эВ}$. Найдите значение максимальной скорости $v_m$ при $r=0$, при которой шарик ещё может быть заперт в потенциальном колодце.

7  ^8.00 Как известно, модули скоростей полистироловых шариков в воде подчиняются распределению Максвелла, которое даётся формулой$$f(v)=4\pi \left( \frac{m}{2\pi kT} \right)^{\frac{3}{2}} v^2 e^{-\frac{mv^2}{2kT}},$$где $m$ и $v$ — масса и скорость соответственно, а $T$ — их абсолютная температура. Для двух шариков массами $m$ и $2m$ найдите вероятности быть запертыми в потенциальной яме $P_m$ и $P_{2m}$ соответственно и сравните их.