A1  ^0.60 Определите силу сопротивления $f$, действующую на единицу площади поверхности капли. Ответ выразите через $\rho$, $D$ и $g$.

Будем рассматривать проекцию силы сопротивления на вертикальную ось $y$, направленную против ускорения свободного падения $\vec{g}$.
Для кольца с радиусом $R\sin\theta$ и толщиной $R d\theta$, где $R$ - радиус капли, проекция силы сопротивления $dF_y$ равна:
$$dF_y=f\cdot 2\pi R^2\sin\theta d\theta\cdot \sin\theta\Rightarrow F_y=2\pi{R}^2f\int\limits_0^{\pi}\sin^2\theta d\theta=\pi{R}^2f\int\limits_0^{\pi}(1+\cos 2\theta)d\theta
$$
После интегрирования:
$$F_y=\pi^2R^2f
$$
Приравнивая силу сопротивления и силу тяжести:
$$\pi^2R^2f=\cfrac{4\pi{R}^3\rho g}{3}
$$
находим:

A2  ^1.00 Определите горизонтальную составляющую $F_a$ силы сопротивления воздуха, действующей на четверть сферической поверхности капли в её нижней части, как показано на рис. 3. Ответ выразите через $\rho$, $g$ и $d$.

Введём в центре капли сферическую систему координат таким образом, что капля разделена на две равные части плоскостью $xz$, где ось $x$ - ось, от которой отсчитывается угол $\varphi$. Тогда для элементарной силы в проекции на ось $x$ имеем:
$$dF_x=f\cdot R^2\sin\theta d\theta d\varphi\cdot\cos\theta\cdot\cos\varphi
$$
откуда:
$$F_a=fR^2\int\limits_{0}^{\pi/2}\sin\theta\cos\theta d\theta\int\limits_{-\pi/2}^{\pi/2}\cos\varphi d\varphi=fR^2=\cfrac{fD^2}{4}
$$
Подставляя $f$, находим:

A3  ^0.50 Определите горизонтальную составляющую $F_t$ силы поверхностного натяжения, действующей на четверть сферической поверхности капли в её нижней части, как показано на рис. 3. Ответ выразите через $\sigma$ и $d$.

Сила поверхностного натяжения действует на четверть капли со стороны двух полуокружностей, лежащих в вертикальной и горизонтальной плоскостях. Вклад в горизонтальную сила вносит только полуокружность, лежащая в вертикальной плоскости. Имеем:
$$F_t=\sigma l=\pi R\sigma
$$
откуда:

A4  ^0.40 Считая, что критерием сферической поверхности капли является условие:
$$F_t\geq 100F_a
$$
рассчитайте максимальное значение её диаметра.

Запишем критерий сферической формы поверхности капли:
$$\cfrac{\pi D\sigma}{2}\geq 100\cdot\cfrac{\rho gD^3}{6\pi}
$$
откуда:

B1  ^0.80 Определите угол $\theta$. Ответ выразите через $\alpha$ и $n$.

Определим угол $\varphi$ преломления капли из закона Снэлла:
$$\sin\alpha=n\sin\varphi
$$
Изобразим траекторию луча до преломления в капле, внутри неё и после преломления на рисунке ниже:

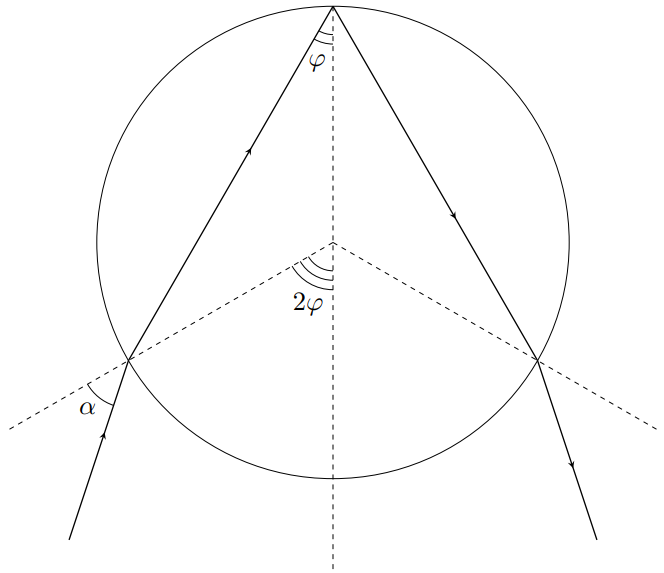
Углы между осью симметрии траектории и линиями, вдоль которых луч движется до преломления в капле и после повторного преломления, одинаковы и равны $2\varphi-\alpha$.
Тогда для $\theta$ имеем:
$$\theta=4\varphi-2\alpha
$$
или же:

B2  ^1.20 Определите угловое распределение интенсивности $J(\theta)$ света, преломлённого в воздух после однократного отражения в капле. Ответ выразите через $I_0$, $D$, $n$, $\alpha$, $T_1$, $T_2$ и $R_e$.

В силу симметрии величина $J$ не зависит от $\varphi$, поэтому для $J(\theta)$ можно записать:
$$J(\theta)=\cfrac{1}{2\pi}\cdot\cfrac{dP}{d\theta}
$$
где $dP$ - доля мощности светового потока, заключённого между углами $\theta$ и $\theta+d\theta$.

Перейдём к решению в терминах угла $\alpha$. Для $d\theta$ имеем:
$$d\theta=\left(\cfrac{\partial \theta}{\partial \alpha}\right)d\alpha=\left(\cfrac{4\cos\alpha}{\sqrt{n^2-\sin^2\alpha}}-2\right)d\alpha
$$
Тогда для $J(\theta)$ имеем:
$$J(\theta)=\cfrac{1}{4\pi(2\cos\alpha/\sqrt{n^2-\sin^2\alpha}-1)}\cdot\cfrac{dP}{d\alpha}
$$
Мощность $dP_0$, падающая на каплю в области круга, ограниченного углами $\alpha$ и $\alpha+d\alpha$, равна:
$$dP_0=2\pi{R}^2I_0\sin\alpha d(\sin\alpha)=2\pi{R}^2I_0\sin\alpha\cos\alpha d\alpha
$$
Рассматриваемые лучи переходят из воздуха в воду, отражаются на границе раздела ''вода — воздух'' и переходят из воды в воздух, поэтому доля вышедшей энергии составляет $T_1T_2R_e$ от энергии падающих лучей:
$$dP=dP_0\cdot T_1T_2R_e
$$
Таким образом:

B3  ^0.50 Для монохроматических источников света с длиной волны $\lambda=550~\text{нм}$ рассчитайте угол $\theta_M$, соответствующий максимуму $J(\theta)$ и максимальное значение $J(\theta_M)$. Показатель преломления воды при $\lambda=550~\text{нм}$ равен $n_g=1{.}3342$.

Обратим внимание, что $J(\theta)=\infty$ при нулевом значении знаменателя.
Определим угол $\theta$, соответствующий ему.
Для угла $\alpha_M$ имеем:
$$4\cos^2\alpha_M=n^2_g-\sin^2\alpha_M\Rightarrow \alpha_M=\arcsin\sqrt{\cfrac{4-n^2_g}{3}}
$$
откуда:

B4  ^0.50 Постройте качественный график зависимости интенсивности спектра солнечного света как функцию длины волны $\lambda$, отраженного вдоль направления $\theta=\theta_M$, найденного в пункте $\mathrm{B4}$, и укажите на графике все характерные значения.

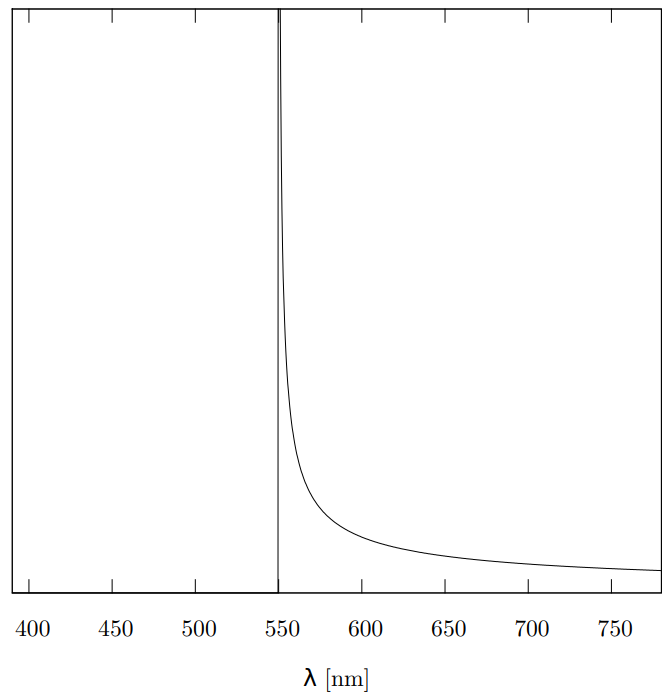
Зависимость $n(\lambda)$ является непрерывной и монотонно убывающей функцией. Обратим внимание, что чем больше значение $n$,тем меньше значение угла $\theta_M$. Это означает, что волны с длинами меньше, чем $550~\text{нм}$ просто не имеют направления $\theta_M$, рассчитанного в пункте $\mathrm{B3}$, и, следовательно, их интенсивность для данного направления равна нулю.

Интенсивность для длин волн, превышающих значение $550~\text{нм}$, при заданном значении $\theta_M$ очень быстро убывает, что отображено на графике ниже.

C1  ^0.80 Вычислите угловой радиус $\theta_0$ и угловую ширину $\Delta\theta$ радуги. Считайте, что солнце находится прямо за наблюдателем.

Угловому радиусу радуги соответствует значение $\theta_M$ для красного света, поэтому:
$$\theta_0=\theta_{Mr}
$$
или же

Для первой компоненты угловой ширины радуги имеем:
$$\Delta{\theta}=\theta_{Mr}-\theta_{Mv}
$$
Для $\theta_{Mv}$ находим:
$$\theta_{Mv}=40{.}52^{\circ}
$$
откуда:
$$\Delta\theta_1=1{.}76^{\circ}
$$
Важно учесть влияние углового размера Солнца:
$$\Delta\theta_2=\delta
$$
откуда получим расчётную формулу для $\Delta\theta$:
$$\Delta\theta=\Delta\theta_1+\Delta\theta_2=\theta_{Mr}-\theta_{Mv}+\delta
$$
или же

C2  ^1.00 Вычислите диаметр $d_m$ наименьшей капли воды, способствующей образованию радуги.

Если дифракционный радиус пятна превышает угловую ширину радуги - капля не вносит вклад в образование радуги.
Поскольку дифракцию можно рассматривать как дифракция на круглом отверстии диаметром $d$ - имеем:
$$\cfrac{1{.}22\lambda}{d}\leq\sin\Delta\theta
$$
откуда:
$$d\geq\cfrac{1.22\lambda}{\sin\Delta\theta}
$$
Минимуму соответствует длина волны фиолетового света $\lambda_v=390~\text{нм}$, откуда:

C3  ^0.70 Если высота нижней границы облаков во время дождя была $800~\text{м}$, рассчитайте максимальное время $T_M$ после прекращения дождя, в течение которого капли воды,  способствующие образованию радуги, все еще могут находиться на высотах выше $200~\text{м}$. Вязкость воздуха равна $\eta=1{.}8\cdot{10^{-5}}~\text{Па}\cdot\text{с}$.

Примечание: на сферическую каплю радиусом $r$, движущуюся с малой скоростью $v$ в среде с вязкостью $\eta$, в соответствии с формулой Стокса действует сила сопротивления, равная:

$$F_\text{сопр}=6\pi r\eta v
$$

Поскольку расстояние, проходимое каплей, порядка нескольких сотен метров — будем рассматривать движение капли с установившейся скоростью.
Имеем:
$$3\pi d\eta v=\cfrac{\pi\rho{d}^3g}{6}
$$
откуда:
$$v=\cfrac{\rho gd^2}{18\eta}
$$
Обозначим перепад высот за $H$:
$$H=800~\text{м}-200~\text{м}=600~\text{м}
$$
Тогда для времени движения $T$ имеем:
$$T=\cfrac{18\eta H}{\rho gd^2}
$$
Максимальное время движения достигается в случае минимального диаметра капли $d_m$, откуда:

C4  ^2.00 Если продолжительность светового дня в этот день составляла $14~\text{часов}$, рассчитайте максимальное время $T_r$ (в часах), в течение которого можно было увидеть радугу в этот день.

Обратим внимание на соотношение $T_M\sim\lambda^{-2}$. Следовательно, для красного света время падения капель $T_{Mr}$ составляет:
$$T_{Mr}=9{.}4~\text{часа}
$$
Это время является теоретически максимально возможным временем, в течение которого видно радугу.

Солнце находится над горизонтом при условии его нахождения над плоскостью, касающейся поверхности Земли в рассматриваемой точке.
Радуга видна при условии нахождения Солнца над горизонтом на угловой высоте, не превышающей угловую ширину радуги.
В точках, близких к полюсам, угловая высота Солнца над горизонтом может оставаться сколь угодно малой, поэтому последнее условие всегда может быть обеспечено, следовательно: