1  ^?? В каком диапазоне могут лежать значения $k$?

Закон сохранения энергии:\[K_1=K'_1+K'_2.\]Поскольку кинетическая энергия обеих частиц после столкновения должна быть неотрицательной $K'_{1,2}\ge0$, то\[0\le\frac{K'_1}{K_1}=1-\frac{K'_2}{K_1}\le1\implies\]

2  ^?? Получите $k(\theta)$ и укажите диапазон возможных значений $\theta$ для произвольного фиксированного $R$. Рассмотрите отдельно случаи $R > 1$, $R=1$ и $R < 1$.

Закон сохранения импульса:\[\vec p_1=\vec p_1'+\vec p_2'.\]Возводим в квадрат:\[p_2^{\prime2}=p_1^2+p_1^{\prime2}-2p_1p_1'\cos\theta.\]Далее, поскольку $p^2=2mK$,\[K_1-2\sqrt{K_1K_1'}\cos\theta+K_1'=R(K_1-K_1')\implies (1+R)k-2\cos\theta\cdot \sqrt k+1-R=0\implies\\\implies \sqrt k=\frac{\cos\theta\pm\sqrt{\cos^2\theta-(1-R^2)}}{R+1}.\]Величина $k$ ограничивается неравенством, полученным в предыдущем пункте. Далее возможны три случая:

• $R > 1$. В этом случае имеет место неравенство:\[\sqrt{\cos^2\theta-(1-R^2)} > |\cos\theta|.\]Чтобы удовлетворить $\sqrt k \ge 0$, необходимо выбрать знак $+$ в выражении для $k$. В этом выражении $\theta$ может принимать любые значения. Итого:

• $R=1$. В этом случае выражение упрощается до $k=\cos^2\theta$ при $\theta < \pi/2$ и $k=0$ при $\theta\ge\pi/2\implies$

• $R < 1$. В этом случае имеет место неравенство:\[\sqrt{\cos^2\theta-(1-R^2)} < |\cos\theta|.\]При $\theta \ge\pi/2$ условие $\sqrt k\ge0$ не выполняется. При $\theta < \pi/2$ условие существования корня:\[\cos^2\theta-(1-R^2) \ge0\implies\cos\theta\ge\sqrt{1-R^2}.\]При этом в ответе возможны оба знака. Итого:

3  ^?? В этой модели выразите $k$ через $R$, $A$ и $b$. Выберите ветви этой функции, рассмотрев частные случаи лобового $(b=0)$ и касательного $(b=A)$ столкновений. Найдите, какой диапазон значений $b$ соответствует каждой из полученных ветвей.

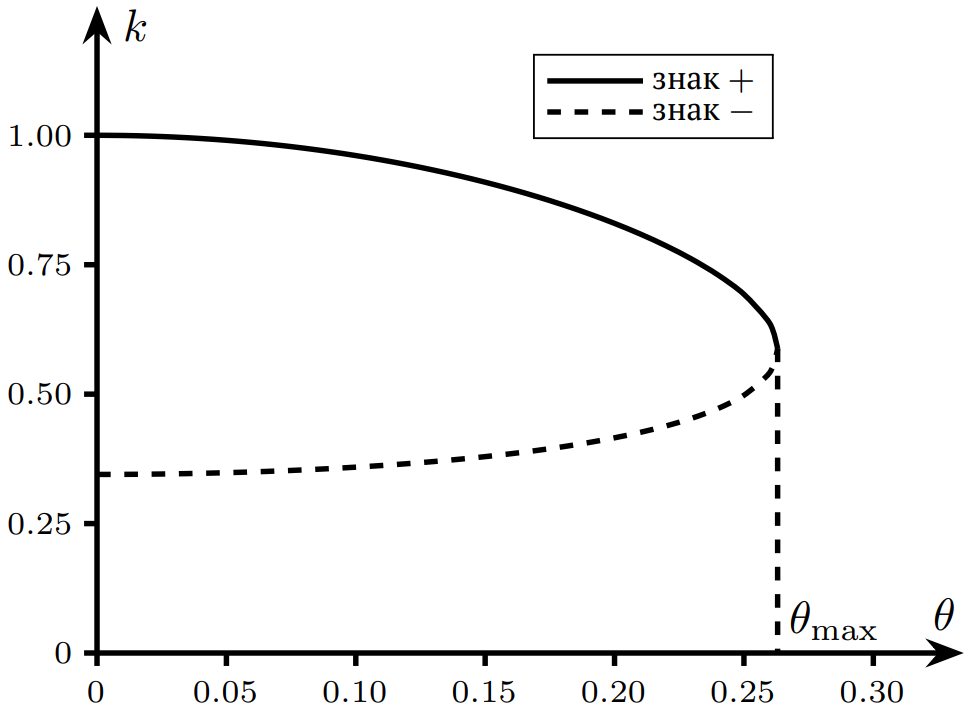
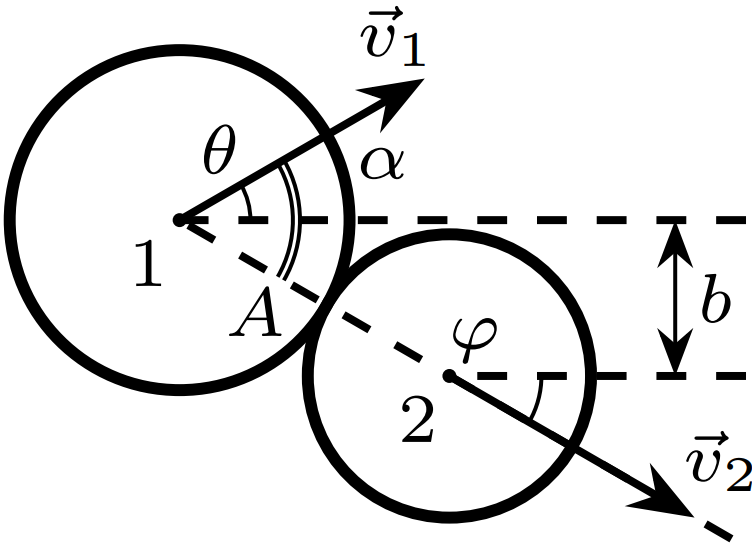
Рассмотрим процесс выбора ветви при $R < 1$. Угол между импульсом $\vec p'_2$ шара 2 после столкновения и начальным импульсом $\vec p_1$ шара 1 обозначим $\varphi$. Прицельный параметр и сумма радиусов шаров будут связаны как:\[b=A\sin\varphi.\]Теорема косинусов:\[p_1^{\prime2}=p_1^2+p_2^{\prime2}-2p_1p'_2\cos\varphi\implies (1+R)\sqrt{1-k}=2\sqrt R\cos\varphi\implies \\\implies k=1-\frac{4R\cos^2\varphi}{(1+R)^2}=1-\frac{4R(1-\sin^2\varphi)}{(1+R)^2}=\frac{(1-R)^2+4Rb^2/A^2}{(1+R)^2}.\]В случае касательного столкновения твёрдых шаров должно быть $k=1$, что соответствует знаку $+$. В случае лобового столкновения $k=\left(\dfrac{1-R}{1+R}\right)^2$, что соответствует знаку $-$. Переход от одной ветви к другой происходит в точке $\theta=\theta_{\max}=\arccos\sqrt{1-R^2}$, в которой\[\sqrt{k_\mathrm {cr}}=\cfrac{\cos\theta_{\max}}{1+R}=\sqrt{\dfrac{1-R}{1+R}}\implies b_{\mathrm{cr}}=\sqrt{\dfrac{1-R}{2}}\,A\implies\]

4  ^?? Найдите выражение для кинематического коэффициента $k(\theta)$. Сравните его с классическим результатом.

Кинетическая энергия частицы:\[K=E-m_0c^2.\]Связь энергии и импульса:\[E^2=m_0^2c^4+p^2c^2.\]Подставляя в закон сохранения импульса, получаем:\[E_{2}^{\prime 2}=E_{1}^{ 2}+E_{1}^{\prime 2}-m_0^{2}c^4-2\sqrt{(E_{1}^{2}-m_0^2c^4)(E_{1}^{\prime 2}-m_0^2c^4)}\cos\theta\implies\\\implies\cos\theta=\sqrt{\dfrac{(E_1+m_0c^2)(E'_1-m_0c^2)}{(E_1-m_0c^2)(E'_1+m_0c^2)}}=\sqrt{\dfrac{(K_1+2m_0c^2)K'_1}{K_1(K'_1+2m_0c^2)}}\implies\]

5  ^?? Как связаны между собой $K'_1$ и угол $\alpha$ между направлениями движения частиц после столкновения? При каком $K'_1$ функция $\alpha(K'_1)$ имеет экстремум? Какой это экстремум (минимум или максимум) и чему равно экстремальное значение $\alpha$? Чему при этом равен $\theta$?

Закон сохранения импульса:\[p_1^2=p_1^{\prime2}+p_2^{\prime2}+2p'_1p'_2\cos\alpha\implies (E'_1-m_0c^2)(E'_2-m_0c^2)=\sqrt{(E_1^{\prime2}-m_0^2c^4)(E_2^{\prime2}-m_0^2c^4)}\,\cos\alpha\implies\\\implies\cos\alpha=\sqrt{\frac{ (E'_1-m_0c^2)(E'_2-m_0c^2)}{ (E'_1+m_0c^2)(E'_2+m_0c^2)}}=\sqrt{\frac{K'_1(K_1-K'_1)}{(K'_1+2m_0c^2)(K_1-K'_1+2m_0c^2)}}\implies\]

Экстремум найдём, приравняв к нулю производную:\[0=\frac{\mathrm d\cos\alpha}{\mathrm dK'_1}=\frac{(K_1+2m_0c^2)(K_1-2K'_1)m_0c^2}{\left[(K'_1+2m_0c^2)(K_1-K'_1+2m_0c^2)\right]^{3/2}}\implies\]

Поскольку $\dfrac{\mathrm d^2\cos\alpha}{\mathrm dK_1^{\prime2}} < 0$, этот экстремум —

Подставляем $K'_1=\dfrac{1}{2}K_1$:\[\cos\alpha_{\min}=\frac{K_1}{K_1+4m_0c^2}\implies\]

Подставляя $K'_1=\dfrac{1}{2}K_1$ в выражение, полученное в предыдущем пункте, получим:\[\cos^2\theta=\frac{K_1+2m_0c^2}{K_1+4m_0c^2}=\frac{1}{2}\big(1+\cos\alpha_{\min}\big)\implies \theta=\alpha_{\min}/2\implies\]