
Поле в системе отсчёта $S'$:\[E_{y'}=\frac{v_0}{\sqrt{1-\beta^2}}B_0\cos\left(\frac{2\pi}{\Lambda}z\right),\quad B_{x'}=\frac{1}{\sqrt{1-\beta^2}}B_0\cos\left(\frac{2\pi}{\Lambda}z\right),\]где $\beta=v_0/c$. Из преобразований Лоренца для координат следует\[z=\frac{z'+v_0t'}{\sqrt{1-\beta^2}}.\]Итого:\[E_{y'}=\frac{v_0}{\sqrt{1-\beta^2}}B_0\cos\left(\frac{2\pi}{\Lambda}\frac{z'+v_0t'}{\sqrt{1-\beta^2}}\right),\quad B_{x'}=\frac{1}{\sqrt{1-\beta^2}}B_0\cos\left(\frac{2\pi}{\Lambda}\frac{z'+v_0t'}{\sqrt{1-\beta^2}}\right).\]Поскольку в этой системе отсчёта пространственная амплитуда колебаний электронов мала, действующее на них поле можно брать в точке $z'=0$, поэтому:\[E_{y'}=\frac{v_0B_0}{\sqrt{1-\beta^2}}\cos\omega't',\quad B_{x'}=\frac{B_0}{\sqrt{1-\beta^2}}\cos\omega't',\]где $\omega'=\frac{2\pi v_0}{\Lambda\sqrt{1-\beta^2}}$. Начальные условия для электрона:\[(x',y',z')=(0,0,0),\quad (v_{x'}(0),v_{y'}(0),v_{z'}(0))=(0,0,0).\]Поскольку в системе отсчёта $S'$ движение электрона будет нерелятивистским, уравнения движения имеют вид:\[\begin{cases}m_e\frac{\mathrm d^2y'}{\mathrm dt^{\prime2}}=-e\frac{v_0B_0}{\sqrt{1-\beta^2}}\cos\omega't'-e\frac{B_0}{\sqrt{1-\beta^2}}\frac{\mathrm dz'}{\mathrm dt'}\cos\omega't'\\m_e\frac{\mathrm d^2z'}{\mathrm dt^{\prime2}}=e\frac{B_0}{\sqrt{1-\beta^2}}\frac{\mathrm dy'}{\mathrm dt'}\cos\omega't'\\m_e\frac{\mathrm d^2x'}{\mathrm dt^{\prime2}}=0\end{cases}.\]Поскольку $\frac{\mathrm dz'}{\mathrm dt'}\ll v_0$, то первое уравнение упрощается до:\[m_e\frac{\mathrm d^2y'}{\mathrm dt^{\prime2}}=-e\frac{v_0B_0}{\sqrt{1-\beta^2}}\cos\omega't'\implies\]
Подставляя ответ для $y'(t')$ в уравнение на $z'$, получим:
Построим параметрически траекторию электрона. Результат показан на рисунке ниже.
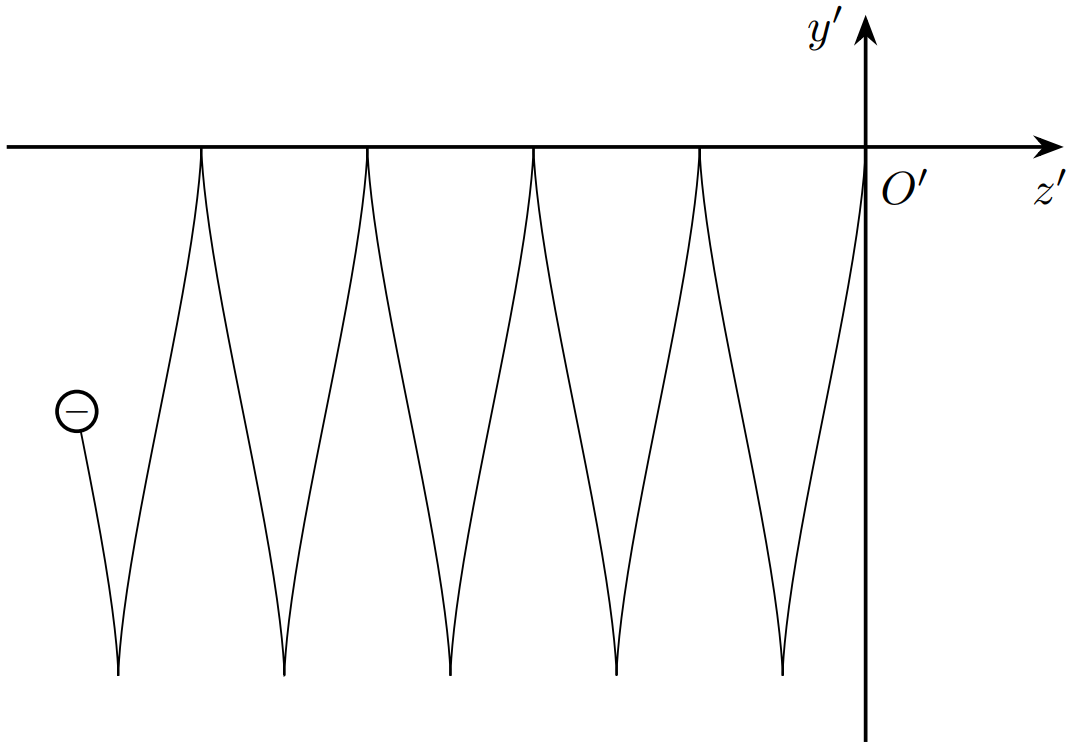
Рентгеновское излучение порождается в результате колебаний электронов вдоль оси $y'$, поэтому угловая частота излучения в системе отсчёта $S'$ равна:\[\omega'=\frac{2\pi v_0}{\Lambda\sqrt{1-\beta^2}}.\]В лабораторной системе отсчёта $S$ частота излучения, согласно релятивистскому эффекту Доплера:\[\omega=\frac{2\pi c}{\lambda}=\sqrt{\frac{1+\beta}{1-\beta}}\omega'=\frac{2\pi v_0}{\Lambda(1-\beta)}\implies v_0=\frac{\Lambda}{\Lambda+\lambda}c\approx\left(1-\frac{\lambda}{\Lambda}\right)c.\]Ускоряющее напряжение:\[eU=\left[\frac{1}{\sqrt{1-\beta^2}}-1\right] m_ec^2\approx m_ec^2\sqrt{\frac{\Lambda}{2\lambda}}\implies \]
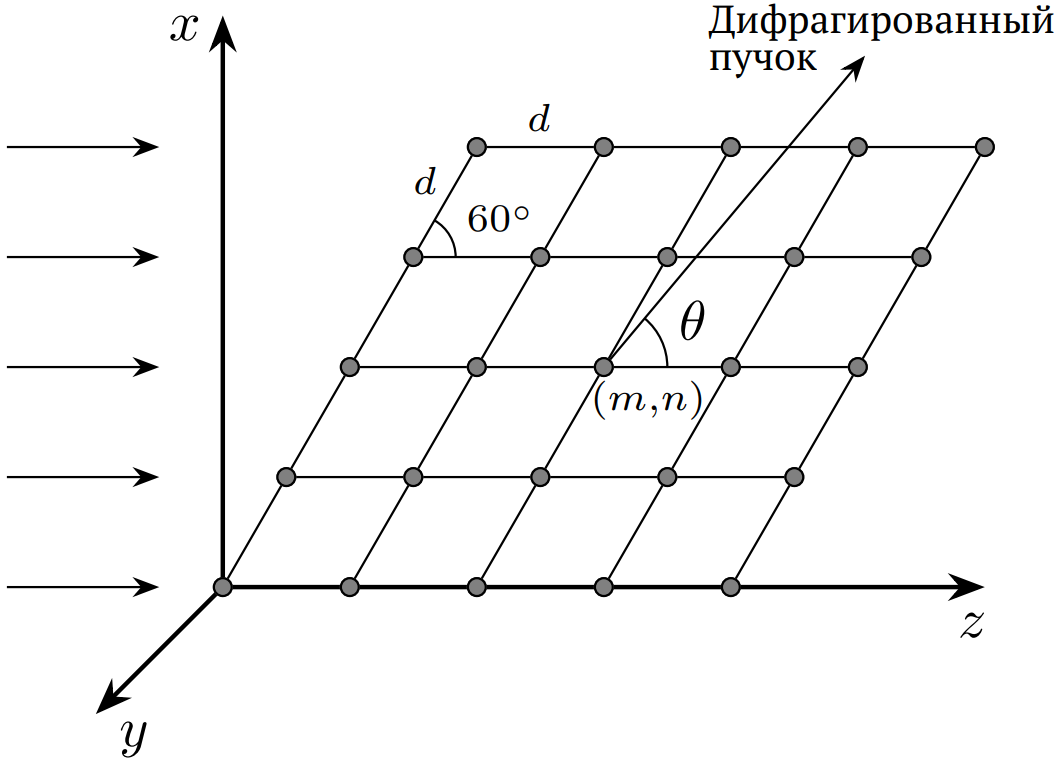
\[E(\theta)=\sum_{m=0}^{N_1-1}\sum_{n=0}^{N_2-1}E_{mn}(\theta)=E_{0}\sum_{m=0}^{N_1-1}e^{-2im\beta_1}\sum_{n=0}^{N_2-1}e^{-2in\beta_2}=E_0e^{-i(N_1-1)\beta_1-i(N_2-1)\beta_2}\frac{\sin N_1\beta_1}{\sin\beta_1}\frac{\sin N_2\beta_2}{\sin\beta_2}.\]Интенсивность излучения:\[\mathcal J(\theta)=|E_0^2|\left(\frac{\sin N_1\beta_1}{\sin\beta_1}\right)^2\left(\frac{\sin N_2\beta_2}{\sin\beta_2}\right)^2.\]Таким образом, условия максимума:\[\beta_{1,2}=k_{1,2}\pi,\quad k_{1,2}\in\mathbb Z\implies\begin{cases}d\left(\frac{\sqrt3}{2}\sin\theta+\frac{1}{2}\cos\theta-\frac{1}{2}\right)=k_1\lambda\\d(\cos\theta-1)=k_2\lambda\end{cases}\implies\\\implies\begin{cases}-1\le\sin\left(\theta+\frac{\pi}{6}\right)=\frac{1}{2}+k_1\frac{\lambda}{d}\le1\\-1\le\cos\theta=1+k_2\frac{\lambda}{d}\le1\end{cases}\implies\begin{cases}k_1=-3,-2,-1,0,1\\k_2=-4,-3,-2,-1,0\end{cases}.\]Возможные значения косинуса, удовлетворяющие условию на $k_2$:\[\cos\theta=-1,-\frac{1}{2},0,\frac{1}{2},1.\]Условие на $k_1$ перепишем в виде:\[k_1=2\left(\frac{\sqrt3}{2}\sin\theta+\frac{1}{2}\cos\theta-\frac{1}{2}\right)=\pm\sqrt{3-3\cos^2\theta}+\cos\theta-1\implies\]