Введение

Сверхтекучесть — это свойство жидкости течь без трения. Повседневный опыт говорит нам, что при движении обычной жидкости (например, воды при комнатной температуре) всегда возникает вязкое трение, приводящее к диссипации энергии так, что поток постепенно замедляется, если он не поддерживается внешними силами. Напротив, сверхтекучая жидкость не теряет кинетической энергии: однажды возбужденное движение сверхтекучей жидкости может продолжаться бесконечно долго. Сверхтекучесть была первоначально экспериментально обнаружена в жидком гелии.
Мы будем рассматривать свойства сверхтекучего гелия при нулевой температуре. Будем считать, что это несжимаемая жидкость с плотностью $\rho$, которая обладает свойством непрерывности (масса втекающая в заданный бесконечно малый объем, и вытекающая из него, одинакова). Это позволяет утверждать, что поток вектора скорости гелия $\vec v$ через любую замкнутую поверхность всегда равен нулю. Отсюда можно сделать вывод, что скорость сверхтекучей жидкости аналогична индукции магнитного поля. Аналогично линиям индукции магнитного поля, ”линии тока” в каждой своей точке направлены по касательной к скорости и их плотность пропорциональна величине скорости.
Истинное сверхтекучее движение является безвихревым, т.е. циркуляция вектора скорости по любому замкнутому контуру внутри гелия равна нулю $$\int_L \vec v\cdot d\vec l = 0$$
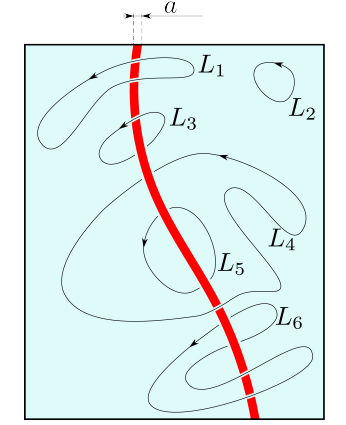
Однако это выражение необходимо изменить, если сверхтекучесть отсутствует вдоль тонкой ”вихревой нити” или ”вихря”. Толщина нити имеет приблизительно атомарные размеры $a$, вокруг нее создаются потоки жидкости на больших расстояниях (дальняя зона). Циркуляция вектора скорости вокруг такой нити равна кванту циркуляции. $$ \left|\int_L \vec{v} \cdot d \vec{l}\right|=2 \pi \kappa,$$
и равна нулю если контур не охватывает ни одну вихревую нить (см. рис). Это подтверждает аналогию между полем векторов скоростей сверхтекучей жидкости и магнитным полем, создаваемым проводами с током: для полей векторов скоростей выполняется принцип суперпозиции (сумма двух полей скоростей также дает поле скоростей), и скорость в любой точке равна (с точностью до размерного коэффициента) индукции магнитного поля, создаваемого электрическими токами, текущими через систему проводов, соответствующих вихревым нитям.

Задание А. Покоящийся вихрь

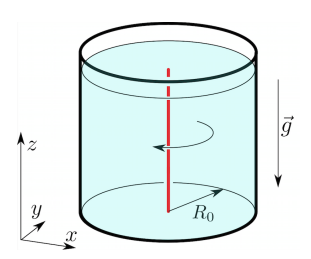
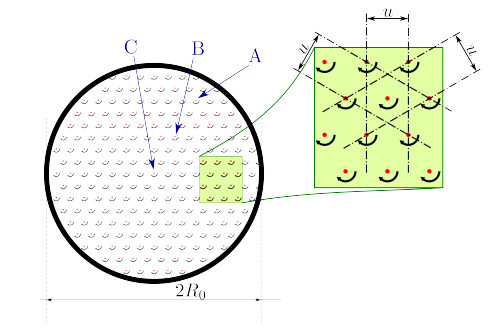
Рассмотрим цилиндрический сосуд (радиусом $R_0\gg a$) со сверхтекучим гелием и прямой вертикальной вихревой нитью в ее центре (см. рис)

A1  ^0.25 Нарисуйте линии тока. Найдите скорость $v$ в точке с радиус-вектором $\vec r$.

A2  ^0.50 Найдите форму свободной поверхности, которая образуется вокруг вихревой нити, т.е. зависимость высоты от расстояния до оси $z(\vec r)$. Ускорение свободного падения $g$. Поверхностным натяжением можно пренебречь.

Задание В. Движущиеся вихри

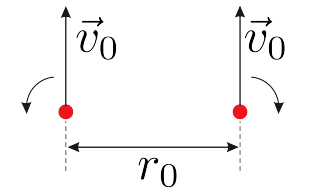
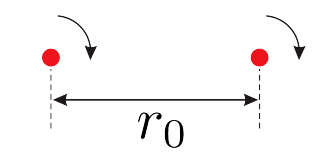
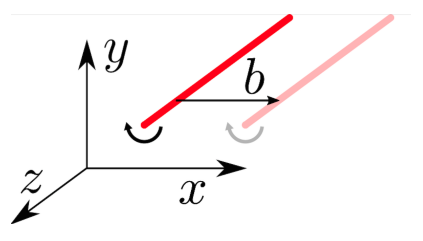
Свободные вихри двигаются в пространстве вместе с потоком. Другими словами, каждый элемент вихревой нити движется со скоростью $\vec v$, равной скорости жидкости, которая должна была быть на месте этого элемента. Для примера, рассмотрим два вихря, вращающихся противоположно друг другу и расположенных на некотором заданном начальном расстоянии $r_0$ друг от друга (см. рис). Каждый вихрь создает движение жидкости со скоростью $v_0=\kappa/r_0$ в точке, в которой располагается ось другого вихря. В результате, эти два вихря движутся прямолинейно и с постоянной скоростью $v_0=\kappa/r_0$, поэтому расстояние между ними не изменяется.

B1  ^0.25 Рассмотрим два одинаковых вихря, которые вначале расположены на расстоянии $r_0$ друг от друга, как показано на рис. Найдите начальные скорости вихрей и изобразите их траектории.

Цилиндрическая емкость с гелием (см. Задание A), заполнена треугольной решеткой ($u\ll R_0$) из одинаковых вертикальных вихревых нитей (см. рис).

B2  ^0.15 Нарисуйте траектории вихрей $\mathrm A, \mathrm B$ и $\mathrm C$ (расположенного в центре).

B3  ^0.40 Найдите скорость $v(\vec r)$ вихря расположенного в точке с радиус-вектором $\vec r$.

B4  ^0.35 Найдите зависимость расстояния $\mathrm A\mathrm B(t)$ между вихрями $\mathrm A$ и $\mathrm B$ от времени $t$. Считайте $\mathrm A\mathrm B(0)$ в начальный момент времени заданным.

B5  ^0.25 Найдите сглаженную форму свободной поверхности гелия $z(\vec r)$, не учитывая решетчатую структуру

Задание С. Импульс и энергия

Поле скоростей в дальней зоне, т.е. расположенных на расстоянии намного большем, чем размер вихря дает основной вклад в энергию системы вихрей. Поэтому она нечувствительна к точной структуре вихревых нитей. Сама вихревая нить не может быть правильно описана макроскопической теорией, поэтому мы считаем, что возникающие сингулярности (бесконечности) несущественны. В действительности, величиной энергии внутри тонкой трубки с радиусом $a$ вокруг вихревой нити можно пренебречь. Вне этой трубки плотность кинетической энергии сверхтекучей жидкости $\rho v^2/2$ (где $\rho = \mathrm{const}$) подобна плотности энергии магнитного поля $B^2/(2\mu_0)$ — они обе квадратичны по соответствующим переменным. Эта аналогия вместе с соответствием между магнитным полем и скоростью сверхтекучей жидкости, а также вихревыми нитями и токами, облегчает расчет кинетической энергии для заданной системы. Например, для случая круговой проволочной петли c током радиусом $R$ с радиусом провода $a$ величина индуктивности $L \approx \mu_0 R \log (R / a)$, отсюда мы получаем энергию сверхтекучей вихревой петли (вихревого кольца) $$U \approx 2 R \rho \pi^2 \kappa^2 \log (R / a)$$ Полный импульс жидкости также определяется распределением скоростей в дальней зоне. Он получается интегрированием плотности импульса $\rho\vec v$. Снова рассмотрим поток, созданный вихревым кольцом, расположенной в плоскости $xy$. Из соображений симметрии очевидно, что полный импульс имеет компоненту отличную от нуля только вдоль оси $z$: $$
P=\int \rho v_z d V=\rho \iint \underbrace{\left(\int v_z d z\right)}_{q(x, y)} d x d y
$$ Внутреннее интегрирование это интегрирование вдоль линий направленных параллельно оси $z$ (см. Рис.). Из тождества $$ \left|\int_L \vec{v} \cdot d \vec{l}\right|=2 \pi \kappa,$$ следует, что внутренний интеграл $$
q(x, y)=\int_{L(x, y)} \vec{v} \cdot d \vec{l}
$$ может принимать только два значения, а именно ноль — для линий проходящих вне кольца и $2\pi\kappa$ для линий проходящих внутри кольца. Поэтому полный импульс равен $$
P=\rho \cdot \pi R^2 \cdot 2 \pi \kappa=2 \pi^2 \rho R^2 \kappa
$$

C1  ^0.30 Рассмотрим вихревую петлю в форме близкой к прямоугольнику с размерами $b\times d, b\ll d$, см. Рис выше. Укажите направление ее полного импульса $\vec P$. Найдите величину полного импульса.

C2  ^0.70 Найдите энергию этой петли $U$.

C3  ^0.75 Предположим, что мы сдвинули длинную прямую вихревую нить на расстояние $b$ в направлении оси $x$, см. Рис. Насколько изменился полный импульс жидкости? Укажите направление изменения полного импульса жидкости. Длина нити (ограниченная стенками сосуда) равна $d$.

Задание D. Захваченные заряды

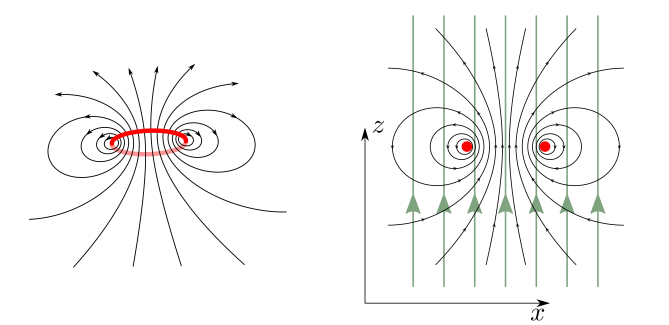
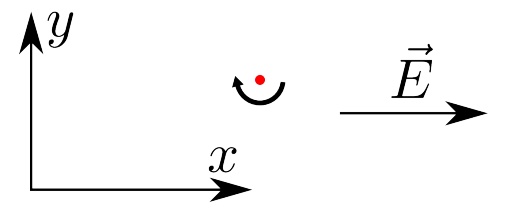
Если электроны поместить в гелий, то они будут ”захвачены” в вихревую нить. Здесь и далее пренебрегаем диэлектрической проницаемостью гелия $(\epsilon = 1)$.

D1  ^0.50 Рассмотрим прямую вихревую нить, заряженную с постоянной линейной плотностью $\lambda<0$ и помещенную в однородное электрическое поле $\vec E$. Изобразите траекторию движения нити. Найдите зависимость ее скорости от времени.

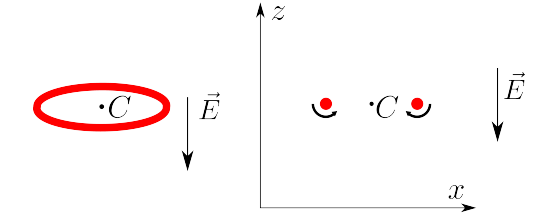
Вихревое кольцо радиуса $R_0$, первоначально с однородно распределенным зарядом с линейной плотностью $\lambda<0$ помещена в однородное электрическое поле $\vec E$ перпендикулярное к ее плоскости и направленное противоположно вектору полного импульса $\vec P_0$.

D2  ^0.60 Нарисуйте траекторию движения центра вихревого кольца $C$. Найдите зависимость радиуса кольца от времени.

D3  ^1.50 Найдите зависимость скорости центра кольца $v(t)$ от времени.

D4  ^0.25 В некоторый момент времени $t^*$, когда скорость достигает значения $v^*=v(t^*)$, электрическое поле выключают. Найдите скорость $v(t)$ вихревого кольца в моменты времени $t>t^*$.

Задание E. Влияние границ

Твердые стенки изменяют поле скоростей, создаваемое вихревой нитью, потому что жидкость не может протекать сквозь них. Математически это означает, что составляющая скорости, направленная перпендикулярно к стенке, обращается в ноль на ее поверхности.

E1  ^0.50 Нарисуйте траекторию прямолинейного вихря, первоначально расположенного на расстоянии $h_0$ от плоской стены. Найдите зависимость скорости от времени.

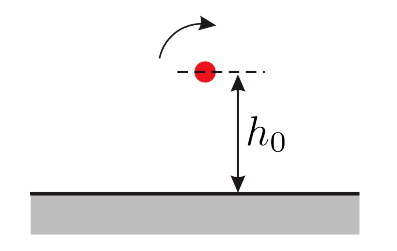
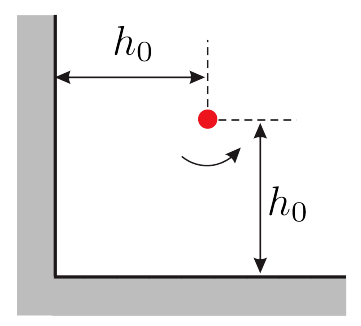
Рассмотрим прямолинейный вихрь расположенный в углу на расстоянии $h_0$ от обеих плоских стенок.

E2  ^0.75 Чему равна начальная скорость $v_0$ вихря?

E3  ^0.50 Изобразите траекторию вихря.

E4  ^1.50 Чему равна скорость вихря $v_{\infty}$ спустя очень большой промежуток времени?