Перейдем в систему отсчета, которая движется со скоростью волнового фронта ударной волны $c$. В этой СО газ с давлением $p_0$ и плотностью $\rho_0$ налетает на неподвижный фронт, а после фронта движется с некоторой скоростью $u$. Во всей задаче будем пользоваться этой системой отсчета.

За время $dt$ через единицу площади потока проходит масса $\rho_0 c dt$, а выходит масса $\rho_1 u dt$, поэтому закон сохранения массы
$$
\rho_0 c = \rho_1 u.
$$Импульс можно получить, домножив массу на соответствующую скорость. При этом импульс газа изменяется при прохождении волнового фронта за счет разности давлений на величину $(p_0 - p_1) dt$, поэтому
$$
(\rho_1 u^2 - \rho_0 c^2 )dt = (p_0 - p_1 )dt,
$$и окончательно
$$
p_0 + \rho_0 c^2 = p_1 + \rho_1 u^2.
$$Исключим скорость $u$ с помощью закона сохранения массы:
$$
u = c \frac{\rho_0}{\rho_1}
$$и получим
$$
p_0 + \rho_0 c^2 = p_1 + \frac{\rho_0^2}{\rho_1} c^2,
$$откуда скорость волны
$$
c = \sqrt{\frac{p_1 - p_0}{\rho_1 - \rho_0} \frac{\rho_1}{\rho_0}}.
$$

Рассмотрим массу $dm$ газа, пересекающую границу. Его кинетическая энергия изменяется на
$$
\Delta E_{\text{к}} = \left( \frac{u^2}{2} -\frac{c^2}{2}\right) dm,
$$внутренняя энергия на
$$
\Delta U = C_V \frac{dm}{\mu} (T_1 - T_0 )= C_V \frac{dm}{R} \left( \frac{p_1}{\rho_1} - \frac{p_0}{\rho_0}\right).
$$Здесь $C_V$ – молярная теплоемкость газа при постоянном объеме, а температура выражена через давление с помощью уравнения состояния идеального газа.

Над газом совершена работа
$$
A =p_0 \frac{dm}{\rho_0} -p_1 \frac{dm}{\rho_1}.
$$Поэтому закон сохранения энергии
\begin{align*}
A &= \Delta E_{\text{к}} + \Delta U, \\
p_0 \frac{dm}{\rho_0} -p_1 \frac{dm}{\rho_1}& = \left( \frac{u^2}{2} -\frac{c^2}{2}\right) dm + C_V \frac{dm}{R} \left( \frac{p_1}{\rho_1} - \frac{p_0}{\rho_0}\right).
\end{align*}
Сократим на массу и перенесем все слагаемые, относящиеся к газу до прохождения волнового фронта в одну сторону:
$$
\frac{p_0}{\rho_0} + \frac{C_V}{R} \frac{p_0}{\rho_0} + \frac{c^2}{2}
=
\frac{p_1}{\rho_1} + \frac{C_V}{R} \frac{p_1}{\rho_1} + \frac{u^2}{2}.
$$Это соотношение – уравнение Бернулли, в котором внутренняя энергия газа выражена через давление и плотность.

Заметим, что
$$
\frac{C_V}{R} + 1 = \frac{C_P}{R} = \frac{C_P}{C_P-C_V} = \frac{\gamma}{\gamma - 1},
$$а также подставим выражение для скорости $u$ через скорость волнового фронта $c$ и получим

Подставим в соотношение из предыдущего пункта выражение для скорости волнового фронта:
$$
\frac{\gamma}{\gamma - 1}\left( \frac{p_1}{\rho_1}- \frac{p_0}{\rho_0}\right) = \frac{1}{2}\left(1-\frac{\rho_0^2}{\rho_1^2} \right) \frac{p_1- p_0}{\rho_1 - \rho_0}\frac{\rho_1}{\rho_0}.
$$Упростим правую часть
$$
\frac{\gamma}{\gamma - 1}\left( \frac{p_1}{\rho_1}- \frac{p_0}{\rho_0}\right) = \frac{\rho_1 + \rho_0}{2\rho_0 \rho_1} (p_1 - p_0) ,
$$сгруппируем слагаемые с $p_0$ и с $p_1$:
$$
p_1\left(\frac{\gamma}{\gamma - 1} \frac{1}{\rho_1} -\frac{\rho_1 + \rho_0}{2 \rho_0 \rho_1} \right) =
p_0\left(\frac{\gamma}{\gamma - 1} \frac{1}{\rho_0} - \frac{\rho_1 + \rho_0}{2 \rho_0 \rho_1} \right),
$$откуда требуемое отношение
$$
\frac{p_1}{p_0}= \frac{\frac{\gamma}{\gamma - 1} \rho_1 - \frac{1}{2}(\rho_0 + \rho_1)}{\frac{\gamma}{\gamma - 1} \rho_0 - \frac{1}{2}(\rho_0 + \rho_1)} = \frac{2 \gamma k - (\gamma -1) (1 + k)}{2 \gamma - (\gamma - 1)(1 + k) }.
$$

Из формулы для предыдущего пункта видим, что давление $p_1$ обращается в бесконечность при $k = \dfrac{\gamma + 1}{\gamma -1}$. Это и есть максимальное значение $k$. Для двухатомного газа $\gamma = 7/5$, $k_{max} = 6$.

Закон сохранения энергии аналогичен пункту $\mathrm{B3}$, но к работе сил давления нужно добавить выделившееся тепло $q dm$ и учесть, что молярные теплоемкости исходного газа и продуктов реакции отличаются :
$$
p_0 \frac{dm}{\rho_0} -p_1 \frac{dm}{\rho_1} + q dm = \left( \frac{u^2}{2} -\frac{c^2}{2}\right) dm + C_{V1} \frac{dm}{R} \frac{p_1}{\rho_1} - C_{V0} \frac{dm}{R} \frac{p_0}{\rho_0}.
$$Выразим теплоемкости газов через показатели адиабаты, скорость газа $u$ через скорость волнового фронта и перегруппируем слагаемые аналогично части A:

В приближении сильной волны скорость волнового фронта
$$
c^2 = \frac{p_1}{\rho_1 - \rho_0} \frac{\rho_1}{\rho_0} = p_1 \frac{v_0^2}{v_0 - v_1}.
$$Подставим его в закон сохранения энергии, пренебрежем при этом слагаемым $\frac{p_0}{\rho_0}$:
$$
q + p_1 \frac{v_0^2}{2(v_0 - v_1)} = \frac{\gamma_1}{\gamma_1 -1}p_1 v_1 + \frac{v_1^2 }{v_0^2} p_1 \frac{v_0^2}{2(v_0 - v_1)} .
$$Отсюда
$$
p_1 \left( \frac{\gamma_1}{\gamma_1 -1} v_1 + \frac{v_1^2 - v_0^2}{2 (v_0 - v_1)}\right) = q,
$$$$
p_1 = \frac{q}{\frac{\gamma_1}{\gamma_1 -1} v_1 - \frac{1}{2} (v_0 + v_1)} = \frac{q}{v_0} \frac{2}{\frac{\gamma_1 + 1}{\gamma_1 -1} \frac{v_1}{v_0} - 1}
$$

График зависимости $p_1(v_1)_{\text{дет}}$ – гипербола, асимптота которой находится при $v_1 = v_0 \dfrac{\gamma_1 -1}{\gamma_1 + 1}$. Зависимость давления от удельного объема, выраженная через скорость звука, имеет вид
$$
p_1(v_1)_{\text{имп}} = \frac{c^2}{v_0} \left( 1 - \frac{v_1}{v_0}\right),
$$ее график - линейная функция, обращающаяся в 0 при $v_1 = v_0$.

Ответ:

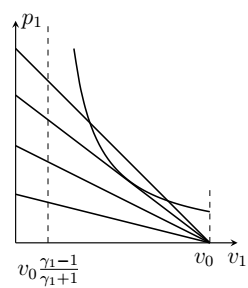
Приравняем выражения для давления через скорость волны и из уравнения ударной адиабаты.
$$
\frac{c^2}{v_0} \left( 1 - \frac{v_1}{v_0}\right)= \frac{2q}{v_0} \frac{1}{\frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1},
$$получим квадратное уравнение на отношение $v_1/v_0$:
$$
\left(1- \frac{v_1}{v_0} \right)\left( \frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1\right) = \frac{2q}{c^2}.
$$Это уравнение будет иметь единственное решение, если правая часть равна максимальному значению квадратичной функции в левой части. Это максимальное значение достигается при
$$
\frac{v_1}{v_0} = \frac{\gamma_1}{\gamma_1 + 1},
$$соответствующее значение равно
$$
\frac{2q}{c^2} = \frac{1}{\gamma_1^2 -1},
$$откуда скорость волны
$$
c = \sqrt{2q (\gamma_1^2 -1)}
$$и давление
$$
p_1 = \frac{c^2}{v_0}\left( 1 - \frac{v_1}{v_0}\right) = \frac{2q (\gamma_1^2-1)}{v_0} \frac{1}{\gamma_1 + 1} = \frac{2q}{v_0} (\gamma_1 -1).
$$

Второе решение. Уравнение будет иметь единственное решение, если кривые зависимости $p_1(v_1)$ будут касаться друг друга. Приравняем выражения для давлений и их производных по $v_1$:

\begin{align*}
&\frac{c^2}{v_0} \left( 1 - \frac{v_1}{v_0}\right)= \frac{2q}{v_0} \frac{1}{\frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1},\\
&\frac{c^2}{v_0^2} = \frac{2q}{v_0^2} \frac{\gamma_1 +1}{\gamma_1 -1}\frac{1}{\left(\frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1\right)^2}.
\end{align*}
Выразим скорость волны из второго уравнения и подставим в первое:
$$
c^2 = 2q \frac{\gamma_1 +1}{\gamma_1 -1}\frac{1}{\left(\frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1\right)^2},
$$$$
\frac{\gamma_1 +1}{\gamma_1 -1}\frac{1 - \frac{v_1}{v_0}}{\left(\frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1\right)^2} = \frac{1}{\frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1},
$$отсюда получаем уравнение на отношение $v_1/ v_0$:
$$
\frac{\gamma_1 +1}{\gamma_1 -1}\left(1 - \frac{v_1}{v_0} \right) = \frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1,
$$из которого находим
$$
v_1 = v_0 \frac{\gamma_1}{\gamma_1 + 1}.
$$Подставляя это значение в выражение для $c^2$, получаем ответы для $c$ и затем $p_1$.

Продукты реакции представляют собой смесь одноатомного, двухатомного и многоатомного газов в равных пропорциях (по количеству вещества), поэтому показатель адиабаты (индексы 1,2,3 отмечают величины, относящиеся к одноатомному, двухатомному и многоатомному газу соответственно)
$$
\gamma_1 = \frac{C_{P1} + C_{P2} + C_{P3}}{C_{V1} + C_{V2} + C_{V3}} = \frac{10}{7}.
$$Тогда скорость волны можно рассчитать по формуле из предыдущего пункта. При этом нужно учесть, что приведено количество тепла, приходящееся на единицу массы водорода. Согласно уравнению реакции, на 1 кг водорода приходится 8 кг кислорода, поэтому нужно использовать значение $q$ в 9 раз меньше.

Запишем закон сохранения энергии из пункта $\mathrm{B2}$, заменив в нем $q = I_0 v_0/c$, выразив скорость волны $c$ через давление и удельные объемы:
$$
I_0 v_0 \frac{\sqrt{1- v_1/v_0}}{\sqrt{p_1 v_0}}+ p_1 \frac{v_0^2}{2(v_0 - v_1)} = \frac{\gamma_1}{\gamma_1 -1}p_1 v_1 + \frac{v_1^2 }{v_0^2} p_1 \frac{v_0^2}{2(v_0 - v_1)} .
$$Преобразуем это уравнение
$$
I_0 \frac{\sqrt{v_0 -v_1}}{\sqrt{p_1}} =\frac{ p_1 v_0}{2} \left( \frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1\right) ,
$$откуда получим

Снова запишем равенство давлений, полученных из формулы для светодетонационной адиабаты и из скорости движения волны:
$$
\left( \frac{2I_0 \sqrt{v_0 -v_1}}{\frac{\gamma_1 +1}{\gamma_1 - 1} v_1 - v_0} \right)^{2/3} = \frac{c^2}{v_0} \left(1 - \frac{v_1}{v_0} \right).
$$Преобразуем это уравнение:
$$
\left(1 - \frac{v_1}{v_0} \right)^{2/3} \left( \frac{\gamma_1 +1}{\gamma_1 - 1} v_1 - v_0 \right)^{2/3} =\frac{ (2 I_0 v_0)^{2/3} }{c^2}.
$$Возводя уравнение в степень $3/2$, снова получим квадратное уравнение на $v_1/v_0$:
$$
\left(1- \frac{v_1}{v_0} \right)\left( \frac{\gamma_1 +1}{\gamma_1 - 1} \frac{v_1}{v_0} - 1\right) = \frac{2I_0 v_0}{c^3}.
$$Левая часть такая же, как и в случае ударной волны, поэтому максимум достигается при
$$
v_1 = \frac{\gamma_1}{\gamma_1 + 1} v_0,
$$а скорость волны можно найти из соотношения
$$
\frac{2 I_0 v_0}{c^3} = \frac{1}{\gamma_1^2 -1}, \quad c = \left(2 I_0 v_0 (\gamma_1^2 -1) \right)^{1/3}.
$$Тогда давление
$$
p_1 = \frac{\left(2 I_0 v_0 (\gamma_1^2 -1) \right)^{2/3}}{v_0} \frac{1}{\gamma_1+ 1} = \left( \frac{4 I_0^2}{v_0}\frac{(\gamma_1 -1)^2}{\gamma_1 + 1}\right)^{1/3}.
$$Для сравнения также построим на одном графике светодетонационную адиабату и зависимости $p_1(v_1) $ при постоянной скорости звука.

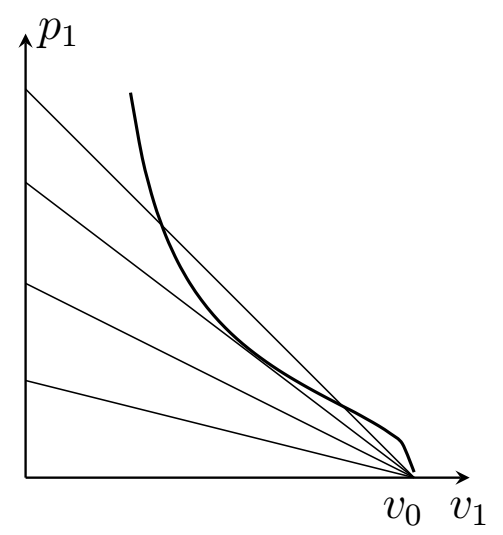
Воспользуемся формулой для скорости волнового фронта из предыдущего пункта, подставим в нее значение интенсивности $I_0 = P/\pi r^2 \sim 10^{15}~\text{Вт}/\text{м}^2$, и значение $v_0 = 1/\rho_0$.