
Как показано на рисунке (a), две параллельных пластины состоят из идеальных проводников, расстояние между ними $d$, и они простираются параллельно в направлении $Oy$. Между пластинами в направлении, перпендикулярном $Oy$, распространяется электромагнитная волна в виде бегущей волны в положительном направлении оси $Ox$. Поле волны может быть записано как$$E=E_0\sin{\left(\frac{2\pi z}{\lambda_z}\right)}\sin{\left(\frac{2\pi x}{\lambda_x}-\omega t\right)},$$ $\omega$ — циклическая частота, $t$ — время, а $\lambda_x$ и $\lambda_z$ — некоторые параметры. С помощью такой системы можно собрать эквивалент антенны, передающей микроволновое излучение. Использование её вместо традиционной крупногабаритной параболической антенны может позволить сэкономить средства, затрачиваемые на её построение.
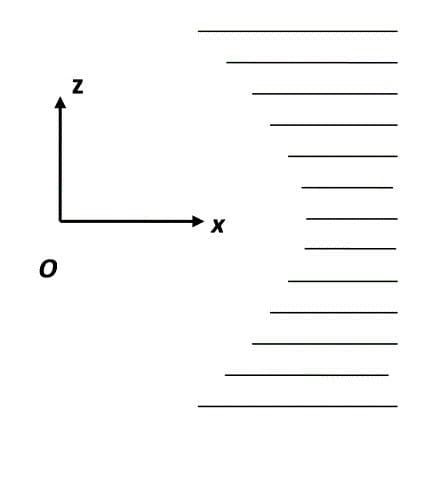
Множество идеально проводящих пластин с одинаковым расстоянием между соседними пластинами расположено симметрично относительно одномерного источника волн, простирающегося бесконечно вдоль направления $Oy$. Правые концы пластин выровнены друг относительно друга, а длины пластин подчиняются некоторому выражению (система показана в разрезе в картинной плоскости на рисунке (b)), так что на правом конце получается распространяющаяся параллельно $Ox$ плоская волна. Считайте, что $m=1$, а расстояние между источником волн и левым концом средней пластины равно $L$.