Введение

Принятые обозначения: Длина вектора $\vec A$ обозначается $A\equiv|\vec A|$. $x$-, $y$- и $z$-компоненты вектора обозначаются как $A_x$, $A_y$ и $A_z$ соответственно.

Производная величины по времени обозначается точкой: $\dot{\vec A}\equiv d\vec A/dt$, $\dot A\equiv dA/dt$. Единичный вектор в направлении $\vec A$ обозначается $\hat A$. Единичные векторы вдоль осей декартовой системы координат, таким образом, — $\hat x$, $\hat y$ и $\hat z$.

Определения скалярного и векторного произведений:

$\left(\vec{A} \cdot \vec{B}\right)=\left(\vec{B} \cdot \vec{A}\right)=A_x B_x+A_y B_y+A_z B_z=A B \cos \theta$

$\left(\vec{A} \times \vec{B}\right)=-\left(\vec{B} \times \vec{A}\right)=\left(A_y B_z-A_z B_y\right) \hat{x}+\left(A_z B_x-A_x B_z\right) \hat{y}+\left(A_x B_x-A_y B_x\right) \hat{z}$

$|\vec{A} \times \vec{B}|=A B \sin \theta$,

где $\theta$ — угол между $\vec A$ и $\vec B$.

Тройные произведения векторов:

$\left(\vec A\times\vec B\right)\times\vec C=\left(\vec A\cdot\vec C\right)\vec B-\left(\vec B\cdot\vec C\right)\vec A$,

$\left(\vec A\times\vec B\right)\cdot\vec C=\left(\vec B\times\vec C\right)\cdot\vec A=\left(\vec C\times\vec A\right)\cdot\vec B$.

Векторные произведения очень полезны при описании многих соотношений в физике. Например:

$\vec v=\vec\omega\times\vec r$,

$\vec F_{Lorentz}=Q\vec v\times\vec B$,

и зачастую экономят время, позволяя записать три уравнения для компонент векторов в одном.

Постановка задачи

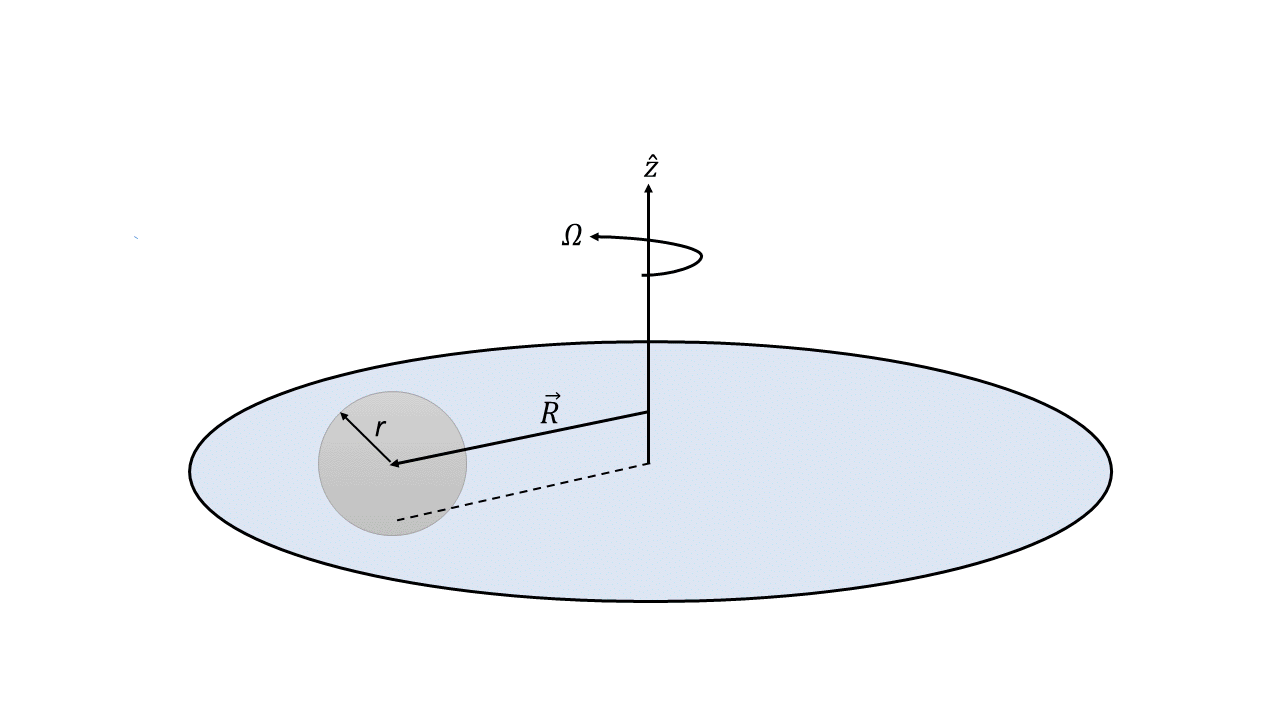
Шарик массой $m$ и радиусом $r$ катится без проскальзывания по горизонтальному вращающемуся диску (см. рис. 1). Его масса распределена сферически симметрично, т.е. плотность зависит только от расстояния до центра. Момент инерции шарика $I$. В части B, в которой диск вращается свободно, момент инерции диска равен $I_d$.

Цель задачи — исследовать движение и траекторию шарика в лабораторной системе отсчёта. При решении задачи считайте диск достаточно большим, и что шарик с него не скатывается. Используются следующие обозначения:

• $\Omega$ — модуль угловой скорости вращающегося диска,
• $\vec\omega$ — угловая скорость шарика относительно его оси вращения,
• $\vec R$ — горизонтальное положение центра шарика относительно оси вращения диска,
• $\vec v$ — скорость шарика в точке $\vec R$ в лабораторной системе отсчёта.

Начальные положение $\vec R_0\equiv\vec R(0)$ и скорость $\vec v_0\equiv\vec v(0)$ шарика, а также угловая скорость диска $\Omega_0\equiv\Omega(0)$ известны.

В векторных выражениях можно использовать орт $\hat z$. Если нужно выразить ответ через известные величины, можно использовать $m$, $r$, $I$ и $I_d$. Подставляйте $I$ в общем виде, если не указано иное.

Также рекомендуется использовать следующие обозначения:

\begin{equation*}\alpha=\frac I{I+mr^2},\quad\delta=\frac{I_d}{mr^2},\end{equation*}

Ответы, представляющие собой векторные величины, можно выражать через векторное и скалярное произведения, а также единичные векторы в направлении осей системы координат.

Часть A. Шарик на диске, вращающемся с постоянной угловой скоростью (1.5 балла)

Рассмотрим сначала простейший случай, когда угловая скорость диска вертикальна и постоянна, т.е. $\Omega=\Omega_0$.

A1  ^0.10 Записав кинематическую связь, выразите скорость шарика $\vec v$ через $\Omega$, $\vec\omega$, $r$ и $\vec R$.

A2  ^0.20 Записав второй закон Ньютона и закон изменения момента импульса относительно центра шарика, выразите ускорение шарика $\vec a\equiv\dot{\vec v}$ через $\Omega$, $\vec v$, $r$, $m$ и $I$.

A3  ^0.20 Выразите скорость $\vec v$ через $\Omega$, $\vec R$, $\vec v_0$, $\vec R_0$, $r$, $m$ и $I$.

A4  ^0.50 Запишите явное выражение для траектории шарика с начальными условиями $\vec v_0$ и $\vec R_0$.

A5  ^0.50 Пусть теперь шарик однороден, т.е. $I=2mr^2/5$. Траектория, найденная в предыдущем пункте, представляет собой круг радиусом $R_t$. Пусть начальные условия подобраны так, что этот радиус равен $R_0$.

Через какое время шарик приблизится к своему исходному положению на диске (в момент времени $t=0$) на минимальное расстояние?

Часть B. Шарик на свободно вращающемся диске (4.0 балла)

В этой части задачи диск может вращаться вокруг оси $z$ без трения. Следовательно, на вращение диска влияет только трение о шарик.

B1  ^0.20 Выразите скорость $\vec v$ и ускорение $\dot{\vec v}$ шарика через $\Omega$, $\vec R$, $\Omega_0$, $\vec R_0$, $\dot\Omega$, $r$, $m$ и $I$.

B2  ^0.60 Выразите модуль углового ускорения диска $\dot\Omega$ через $\Omega$, $\Omega_0$, $\vec R$, $\vec R_0$, $\vec v_0$, $r$, $m$, $I$ и $I_d$. В ответе могут присутствовать величины $\alpha$ и $\delta$, определённые в начале задачи.

B3  ^0.60 Выразите модуль угловой скорости диска $\Omega$ как функцию $R$, а также $\Omega_0$, $R_0$, $r$, $m$, $I$ и $I_d$.

B4  ^0.10 Из результатов пункта B3 получите выражение для максимально возможной $\Omega$ при заданных $\Omega_0$ и $R_0$.

B5  ^2.50 Запишите выражение для вертикальной компоненты момента импульса $\hat zM_z$ всей системы. Некоторые слагаемые в этом выражении — постоянные величины. Вычтя их из $\hat zM_z$, обозначьте оставшееся выражение как $\hat zL$.

Скорость шарика $\vec v$, полученную в пункте B1, можно записать как сумму постоянного вектора и слагаемого, зависящего от $\vec R$. Обозначьте этот постоянный вектор как $\vec c$.

Выберем направление оси $x$ вдоль вектора $\vec{c}$, а направление оси $y$ — вдоль вектора $\hat z\times\vec c$. В этой системе отсчёта выразите $\Omega$ через $L$, $\vec R$, $\vec c$, $\hat z$, $R^2$, $r$, $m$, $I$ и $I_d$.

Добавив к этому результат пункта B3, запишите уравнение, связывающее величины $R^2$ и $y$ с помощью $L$, $r$, $m$, $I$, $c$ и $I_d$. Здесь $c$ — модуль $\vec c$.

Подставив $R^2=x^2+y^2$, запишите выражение, содержащее $x$ и $y$, которое описывает некоторую кривую.

Отсюда найдите и перечислите все возможные типы траекторий шарика.

Часть C. Шарик на вращающемся диске в магнитном поле (4.5 балла)

В этой части задачи рассмотрим шарик, у которого $I=mr^2/10$. Этого можно добиться, если заполнить шарик однородным веществом до половины его радиуса, а оставшуюся часть — пренебрежимо легким веществом.

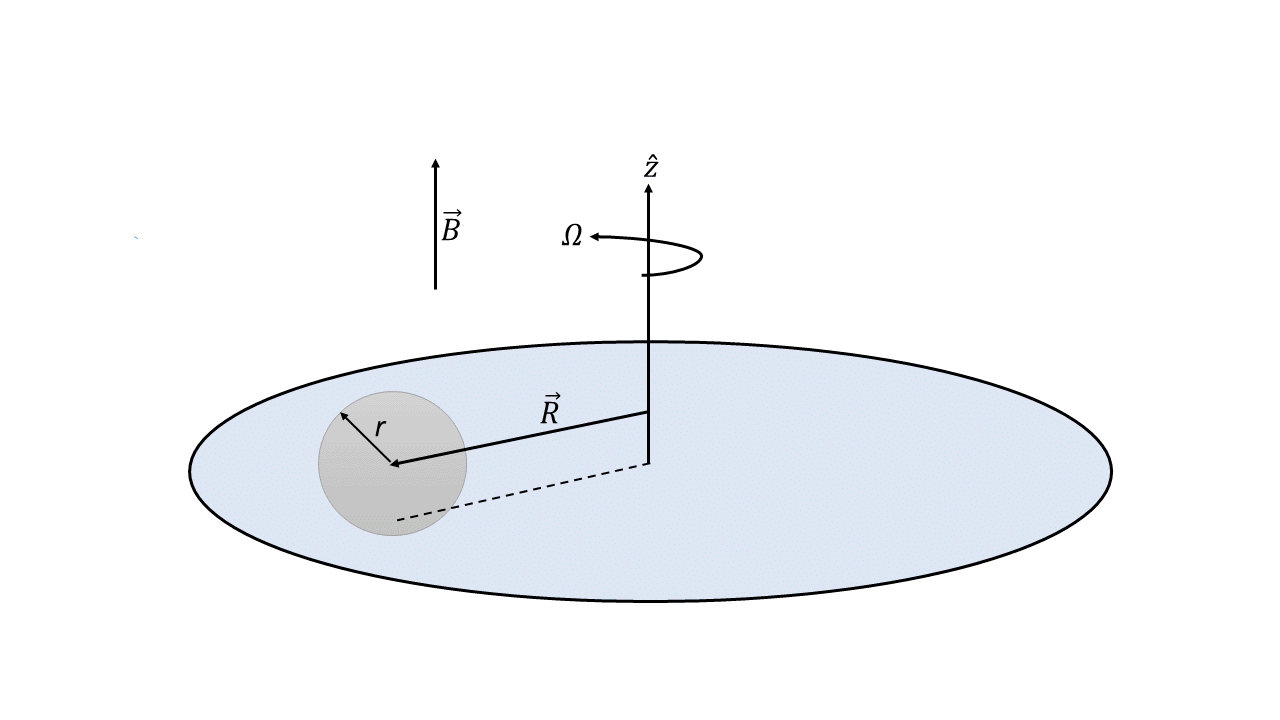
Более того, будем считать, что поверхность шарика заряжена однородно с плотностью заряда $Q/(4\pi r^2)$, где $Q$ — суммарный заряд шарика. Вся система находится в однородном магнитном поле $\vec B$, направленном по оси $\hat z$.

Диск вращается с постоянной угловой скоростью $\Omega$ так же, как в части A.

C1  ^0.50 Запишите второй закон Ньютона и закон изменения момента импульса относительно центра шарика. Выразите момент сил $\vec\tau_s$, действующий на шарик из-за его вращения, через $Q$, $r$, $\vec\omega$ и $\vec B$.

C2  ^0.50 Используя результат пункта C1, выразите линейное ускорение шарика в лабораторной системе отсчёта через $Q$, $r$, $\vec\omega$ и $\vec B$.

C3  ^1.00 Уравнение для линейного ускорения, полученное в пункте C.2, представляет собой дифференциальное уравнение второго порядка на $\vec R$ вида:
\begin{equation*}\frac{d^2\vec R}{dt^2}-\gamma \frac{d\vec R}{dt}\times \hat z+\beta \vec R = 0.\end{equation*}
Выразите постоянные $\gamma$ и $\beta$ через $Q$, $r$, $B$, $I$, $m$, $\Omega$.

Перейдите от компонент $\vec R$ к полярным координатам:
$$\begin{cases} x(t)=\rho(t)\cos(\eta(t)),\\y(t)=\rho(t)\sin(\eta(t)),\end{cases}$$
и получите систему уравнений на $\rho(t)$ и $\eta(t)$, эквивалентную уравнению выше.

Полярный угол $\eta(t)$ представляет собой некоторую функцию времени. Найдите вид этой функции.

Выразите коэффициент $\beta'$ при $\rho(t)$ в полученном вами уравнении на $\rho(t)$ через $\gamma$ и $\beta$.

Запишите условия, при которых реализуются различные характерные зависимости $\rho(t)$: гармоническая, экспоненциальная и т.д.

C4  ^0.90 Рассмотрим следующие начальные условия для решения, найденного в С3:

$x(0)=1~$м, $y=0~$м, $v_x(0)=\dot x|_{t=0}=1~$м/с , $v_y(0)=\dot y|_{t=0}=-1~$м/с.

Найдите $\beta$ и $\gamma$, соответствующие этим начальным условиям. Найдите отсюда соответствующую $\Omega$.

Схематично изобразите траекторию шарика.

Как заряжена поверхность шарика: положительно или отрицательно? Запишите в листах ответов «$-$» в случае отрицательного и «$+$» в случае положительного заряда.

C5  ^1.60 Рассмотрим решение, полученное в пункте C4. Если решение получено правильно, вектор $\vec R$ должен вращаться.

Получите выражения для изменения энергии системы за время $t$ и за один оборот после $N\gg1$ оборотов. Членами малыми по сравнению с $N$ можно пренебречь. В этом пункте можно считать, что масса шарика $m=1~$кг, а его радиус $r=1~$м, поэтому $I=1/10~$кг$\cdot$м${}^2$.