Подключим к трубке шприц. Погрузим свободный конец трубки в воду. Двигая поршень шприца, наберем в трубку $V_0 = (7{,}0\pm0{,}2) \ мл$ воды. Измерим длину столба воды в трубке $h_0=(97{,}1 \pm 0{,}2)$ см (трубка при измерениях должна быть расположена горизонтально).
Рассчитаем площадь поперечного сечения трубки:
$$
S_0=\frac{V_0}{h_0}=(0{,}072\pm0{,}002) \ см^2.
$$
Погрешность измерения оценим, сложив относительные погрешности измерения объема и площади. Заметим при этом, что относительная погрешность измерения длины много меньше относительной погрешности измерения объема.
$$
\sigma_{S_0}=S_0\Big(\frac{\sigma_{V_0}}{V_0}+\frac{\sigma_{h_0}}{h_0}\Big)
$$
Заполнять трубку можно и другим способом: набрать в шприц 10 мл воды, подключить к шприцу пустую трубку и, нажимая на поршень шприца, заполнить трубку водой. Такой способ не является ошибочным. Однако опытным путем можно установить, что при таком способе заполнения в столбике воды в трубке чаще образуются пузыри воздуха, особенно в случае загрязненной внутренней поверхности трубки.
Опустошим трубку. Вновь погрузим свободный конец трубки в воду. Двигая поршень шприца, наберем в трубку приблизительно 4 мл воды. Вытащим свободный конец трубки из воды и переместим с помощью шприца столбик воды ближе к шприцу так, чтобы расстояние от края столбика воды до свободного конца трубки было приблизительно равно длине столбика воды. Вставим в открытый конец трубки пробку. Отключим шприц от трубки. Измерим длину столба воздуха $l_0=(40{,}2\pm0{,}1) \ см$ в трубке, заключенного между местом пережатия трубки и краем столбика воды. Приклеим на поверхность стола мерную ленту, к которой сверху приклеим исследуемую трубку в распрямленном состоянии (см. рис. 2). Подсоединим шприц к оставшемуся открытым концу трубки.

Обозначим координату ближнего к шприцу края столба жидкости в трубке за $x_1$, а дальнего — $x_2$. Будем надавливать на поршень шприца и измерять величины: $x_1$ и $x_2$.
$x_1$, см $x_2$, см $\Delta p, 10^5 \ Па$ $\sigma_{\Delta p}, 10^5 \ Па$ $\frac{\Delta S}{S_0}, \ 10^{-2}$ 4,8 60,2 0,000 0,000 0,00 9,2 64,1 0,097 0,003 0,90 13,2 67,6 0,203 0,005 1,81 16,6 70,5 0,308 0,006 2,71 20,8 74,0 0,462 0,008 3,97 24,4 76,8 0,611 0,011 5,42 29,3 80,5 0,867 0,016 7,58
Объем воды в трубке в течение эксперимента не меняется.
$$
(x_{20}-x_{10})S_0=(x_{2}-x_{1})(S_0+\Delta S),
$$
где $x_{10}$, $x_{20}$ - координаты столба жидкости при атмосферном давлении.
Тогда через изменения длины столбика воды в трубке легко вычислить относительное изменение ее сечения:
$$
\frac{\Delta S}{S_0}=\frac{x_{20}-x_{10}}{x_{2}-x_{1}}-1
$$
Изменение давления в системе можно определить по изменению объема воздуха в трубке, ограниченного столбом воды и местом пережатия трубки. Воспользуемся для этого законом Менделеева-Клапейрона:
$$
p_0 l_0 S_0=p (l_0-(x_2-x_{20})) (S_0+\Delta S).
$$
Тогда для избыточного давления внутри шприца имеем:
$$
\Delta p=p-p_0=p_0\Big(\frac{l_0}{l_0-(x_2-x_{20})}\frac{S_0}{S_0+\Delta S}-1\Big).
$$
Подставляя выражение для отношения площадей получаем:
$$
\Delta p=p-p_0=p_0\Big(\frac{l_0}{l_0-(x_2-x_{20})}\frac{x_{2}-x_{1}}{x_{20}-x_{10}}-1\Big).
$$
Рассчитаем величины относительного изменения сечения трубки и изменения давления в ней.
Погрешность относительного изменения сечения трубки рассчитаем, просуммировав относительные погрешности начальной и текущей длин столбика воды в трубке.
$$
\sigma_{\frac{\Delta S}{S_0}}=\Big(\frac{\Delta S}{S_0}+1\Big)\Big(\frac{2\sigma_x}{x_{10}-x_{20}}+\frac{2\sigma_x}{x_{2}-x_{1}}\Big)
$$
где $\sigma_x = 0{,}5 \ мм$ - половина цены деления шкалы мерной ленты.
С учетом того, что $\frac{\Delta S}{S_0}\ll 1$ и $x_{2}-x_{1}\approx x_{10}-x_{20}$ можно сказать, что погрешность относительного изменения сечения практически не меняется и может быть вычислена как:
$$
\sigma_{\frac{\Delta S}{S_0}}=\frac{4\sigma_x}{x_{10}-x_{20}}=0{,}4\cdot10^{-2}
$$
Погрешность изменения давления рассчитаем по следующей формуле:
$$
\sigma_{\Delta p}=(p_0+\Delta p)\Big(\frac{4\sigma_x}{x_{10}-x_{20}}+\frac{\frac{2\sigma_x}{x_2-x_{20}}+\frac{\sigma_{l_0}}{l_0}}{1-\frac{x_2-x_{20}}{l_0}}\frac{x_2-x_{20}}{l_0}\Big).
$$
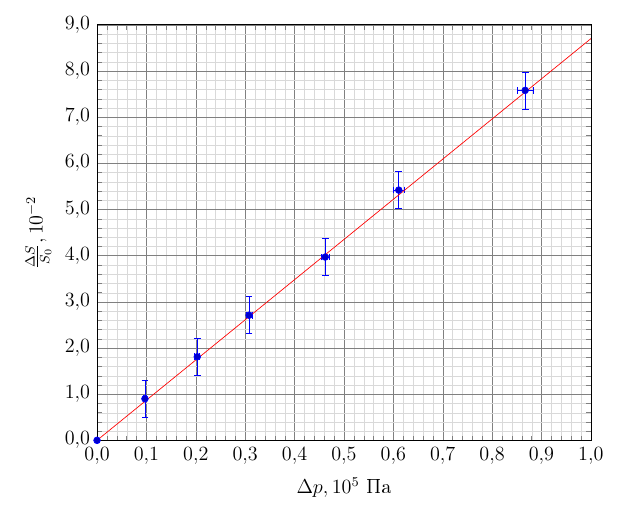
Построим график зависимости $\frac{\Delta S}{S_0}(\Delta p)$. Видно, что график можно описать прямой пропорциональностью с угловым коэффициентом:
$$
\alpha=(8{,}7\pm0{,}3)\cdot 10^{-7} \ Па^{-1}.
$$
Относительная ошибка измерения $\alpha$ составляет $\varepsilon_\alpha\approx3{,}4\%$.
Можно предположить, что учет изменения сечения трубки для подсчета давления в системе, мало повлияет на расчетную величину $\alpha$. То есть провести расчет избыточных давлений по формуле:
$$
\Delta p=p-p_0=p_0\Big(\frac{l_0}{l_0-(x_2-x_{20})}-1\Big).
$$
Однако величина $\alpha$, полученная при таком способе расчета, будет отличаться от результата, полученного с учетом изменения площади сечения, на $\approx15\%$, что существенно превышает рассчитанную относительную ошибку измерения.
Заметим, что измерение давления в системе можно проводить, наблюдая за количеством воздуха в шприце. Для этого необходимо часть шприца заполнить водой, а в части шприца оставить воздух. Далее создавать давление в системе необходимо будет, держа шприц вертикально и надавливая на его поршень. Часть воды из шприца будет поступать в трубку, а воздух в верхней части шприца будет сжиматься под действием давления. Измеряя отношение объема воздуха в шприце под давлением к начальному объему воздуха в нем, можно рассчитать давление в системе. Длина столба воздуха в таких измерениях существенно меньше возможной длины столба воздуха в трубке. Поэтому этот способ измерения давления обладает гораздо меньшей точностью. Также заметим, что стенки шприца достаточно жесткие, однако, если заполнить его водой полностью и попробовать сдвинуть поршень при заткнутом носике, то поршень все же немного сдвинется. Это происходит из-за деформации резиновой прокладки между поршнем и резервуарной частью шприца. Этот эффект меньше цены деления шприца, поэтому им можно пренебречь.