1  ^?? Определите поверхностную плотность (массу единицы площади) $\rho_{S}$ картона.

Из листа картона вырезаем несколько квадратов (прямоугольников) с известными сторонами, вычисляем их площади, взвешиваем на весах и определяем массы.

Возможный вариант реализации: нарисуем квадрат со стороной $10 {~} см$, определяем массу, вдоль одной стороны отрезаем полоску шириной $1 {~} см$, получаем прямоугольник $10 {~} см * 9 {~} см$, взвешиваем, вдоль другой стороны отрезаем полоску шириной $1 {~} см$, получаем квадрат со стороной $9 {~} см$, взвешиваем, и т.д.

Результаты измерений приведены в таблице.

$a, см$	$b, см$	$S = ab, см^2$	$m, г$
10	10	100	3,02
10	9	90	2,66
9	9	81	2,45
9	8	72	2,12
8	8	64	1,91
8	7	56	1,72
7	7	49	1,44
7	6	42	1,25
6	6	36	1,10
6	5	30	0,94
5	5	25	0,76
5	4	20	0,62
4	4	16	0,47
4	3	12	0,35
3	3	9	0,26

Построим график зависимости массы фигуры $m$ от площади $S$.

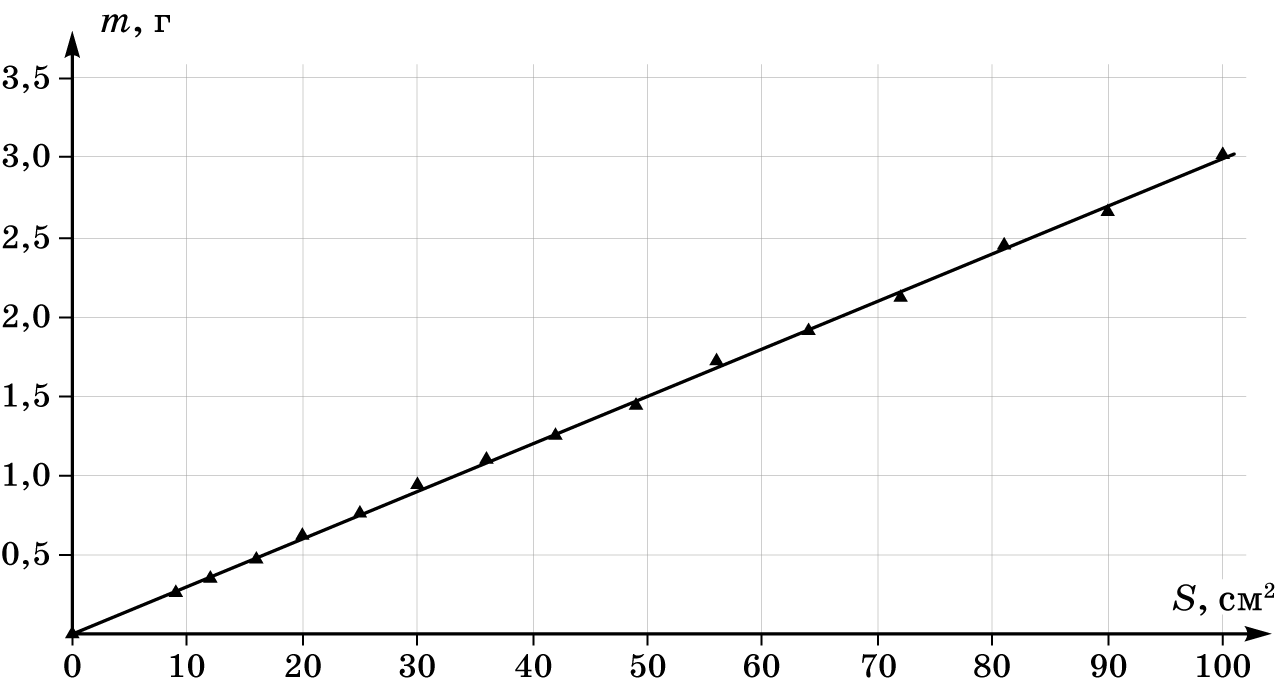
Масса фигур связана с их площадью следующим соотношением: $m = \rho_S S$. Тогда с помощью углового коэффициента наклона графика найдем поверхностную плотность картона:
$$\rho_S = \frac{\Delta m}{\Delta S} = \frac{3,0-0,3}{100-9}=0,03 {~} \frac{г}{см^2} = 0,30 {~} \frac{кг}{м^2} $$

2  ^?? Определите толщину $h$ картонного листа. Получите формулу связи поверхностной и объёмной плотностей и рассчитайте объёмную плотность. Определите объёмную плотность (массу единицы объема) картона $\rho_{V}$. В задании 2 не требуется построение графиков.

Для того, чтобы определить объёмную плотность картона, нужно определить толщину листа $h$. Сделать это можно методом рядов. Из остатков картона нарежем куски, сложим их друг на друга, хорошо прижмём к столу для устранения воздушных зазоров и определим высоту получившегося столбика.
Толщина листа оказывается равной
$$h=0,35 {~} мм$$.

Объемная плотность $\rho_V$ равна
$$\rho_V = \frac{\rho_S}{h} =\frac{0,03}{0,035} = 0,86 \frac{г}{см^3} = 860 \frac{кг}{м^3}$$

3  ^?? Определите коэффициент $k$ из формулы площади эллипса.

На листе картона, используя метод, описанный в условии, рисуем несколько эллипсов. Измеряем большую и малую оси эллипса, производим измерения массы. Представляется разумным все эллипсы рисовать один внутри другого, используя проведённые перпендикулярные линии для измерения длин осей. Сначала вырезается самый большой эллипс, измеряем $A$, $B$ и $m$, затем вырезаем эллипс поменьше и т.д.

$A, см$	$B, см$	$\frac{AB}{4}, см^2$	$m, г$
15,8	13,8	54,5	5,12
14,3	11,9	42,5	4,11
12,7	10,0	31,8	3,00
10,8	7,5	20,3	1,91
10,4	6,3	16,4	1,49
8,8	5,5	12,1	1,13
7,4	4,9	9,1	0,84
6,1	3,4	5,2	0,49

Построим график зависимости массы эллипса $m$ от комбинации $\frac{AB}{4}$.

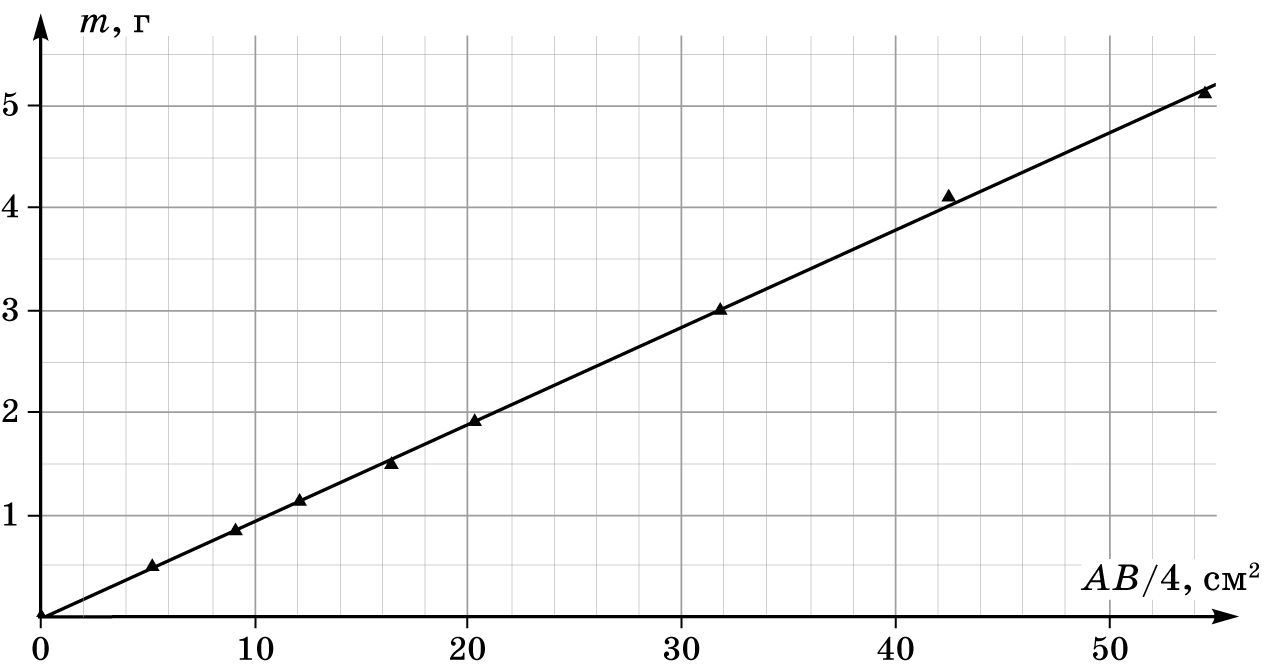
Масса эллипса $m$ связана с его площадью $S$ следующим образом
$m= \rho_S S$, а так как площадь $S$ определяется как $S= \frac14kAB$, то масса равна $m = \rho_S k \frac{AB}{4} = C \frac{AB}{4} $
Угловой коэффициент наклона графика равен $$C = \frac{\Delta m}{\Delta (\frac{AB}{4})} = \frac{5,1 - 0,5}{55 - 5} = 0,092 \frac{г}{см^2} = 0,92{~} \frac{кг}{м^2} $$
Определяем коэффициент $k$:
$$C= \rho_Sk$$
$$k = \frac{C}{\rho_S} = \frac{0,092}{0,03} \approx 3,1$$
Теоретическое значение коэффициента $k$ - знаменитое иррациональное число "пи" $\pi = 3,14...$