Pho.rs: Плотность изоленты

1 ^?? толщину $h$ изоленты;

Отрежем от листа бумаги белые края, оставив только миллиметровую сетку. Размеры получившегося листа бумаги $a=(20,0\pm0,1){~}см,{~}b=(28,0\pm0,1){~}см$. Скрутим миллиметровку в максимально плотную трубочку (разлиновкой наружу) вдоль длинной стороны $b$. Закрепим края очень узкими полосками изоленты, отрезанными от основного рулона. Эту трубочку будем использовать как линейку и как рычаг. Масса трубочки $$M=ab\sigma=4,48\pm0,04{~}г.$$ Измерим трубочкой ширину изоленты $l=(19\pm1){~}мм$, внешний диаметр рулона $D=(72\pm1){~}мм$, внутренний диаметр рулона (без учета картонной втулки) $d=(44\pm1){~}мм$. Объем рулона изоленты можно выразить через его длину $L$, толщину $h$, ширину $l$: \[V=Lhl,\tag{1}\] а также через внешний $D$ и внутренний $d$ диаметры и толщину $l$ рулона: \[V=\frac{\pi(D^2-d^2)}{4}\cdot l.\tag{2}\] Из $(1)$ и $(2)$ $$h=\frac{\pi(D^2-d^2)}{4L}=(127\pm9){~}мкм.$$

Ответ: $h=(127\pm9){~}мкм.$

Заводское значение толщины изоленты 0,13 мм.

2 ^?? линейную плотность изоленты $\lambda$ (массу единицы длины);

Для выполнения второго и третьего пунктов задания необходимо измерить массу изоленты. В данной задаче это может быть осуществлено только с помощью известной массы листа миллиметровой бумаги. Используем изготовленную ранее бумажную трубочку в качестве рычага. Подвесим ее на нитке и определим положение центра масс, уравновесив трубочку в горизонтальном положении. Далее будем отрезать от изоленты отрезки длиной $b = 28{~}см$ (равные длине бумажного рычага) и последовательно наматывать их заподлицо на край бумажной трубочки (см. рисунок). Обозначим массу одного отрезка $m_0$. Снимем зависимость смещения $x$ центра масс системы «рычаг + лента» от количества $n$ отрезков изоленты длиной $28{~}см$, намотанных на рычаг. Ниже приведена таблица измерений.

$n$	$x,{~}мм$	$\frac{1}{n}$	$\frac{1}{x},{~}\frac{1}{м}$
$1$	$20\pm1$	$1,00$	$50,0\pm2,5$
$2$	$36\pm1$	$0,50$	$27,8\pm0,8$
$3$	$47\pm1$	$0,33$	$21,3\pm0,5$
$4$	$56\pm1$	$0,25$	$17,9\pm0,3$
$5$	$63\pm1$	$0,20$	$15,9\pm0,3$

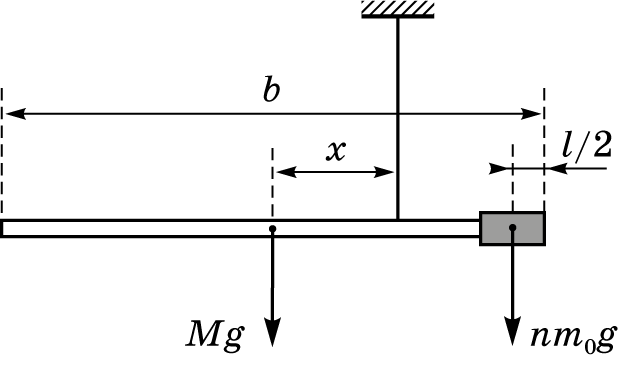
Запишем правило моментов относительно точки подвеса для системы в горизонтальном положении рычага \[Mgx=nm_0g\left(\frac{b}{2}-\frac{l}{2}-x\right).\tag{3}\] После преобразований \[\frac{1}{n}=\frac{1}{x}\cdot \frac{m_0}{M}\left(\frac{b-l}{2}\right)-\frac{m_0}{M}.\tag{4}\] Видно, что зависимость $\frac{1}{n}$ от $\frac{1}{x}$ является линейной. Угловой коэффициент $k$ этой зависимости дает возможность определить $m_0$ – массу отрезка изоленты длиной $28{~}\text{см}$. Построим график $\frac{1}{n}$ от $\frac{1}{x}$.

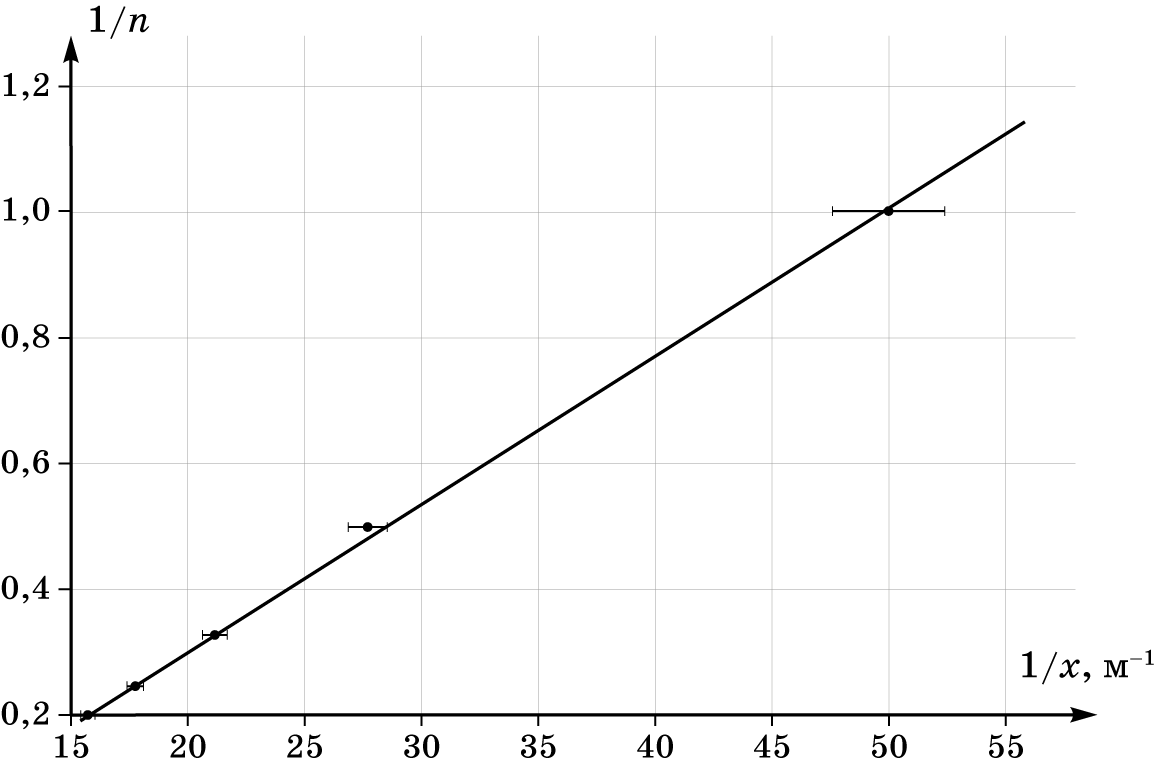
С помощью графика находим $$k=\frac{m_0}{M}\left(\frac{b-l}{2}\right)=\left(24,4\pm1,2\right){~}мм$$ или $m_0=(0,84\pm0,06){~}г$. Линейная плотность изоленты $$\lambda=\frac{m_0}{b}=(3,0\pm0,2){~}\frac{г}{м}.$$

Ответ: $\lambda=(3,0\pm0,2){~}\frac{г}{м}.$

3 ^?? объемную плотность изоленты $\rho$ (массу единицы объема).

Объемная плотность изоленты $$\rho=\frac{\lambda}{hl}=(1,24\pm0,24){~}\frac{г}{{см}^3}.$$

Ответ: $\rho=(1,24\pm0,24){~}\frac{г}{{см}^3}$.

Примечание: если в решении участников олимпиады из правила моментов (3) получена зависимость $\frac{1}{n}$ от $\frac{1}{x}$ (выражение (4)), то удобнее и вполне допустимо построение графика именно этой зависимости, т.е. по горизонтали откладывается обратная величина измеряемой величины, а по вертикали – изменяемой. Если же учащийся после преобразований из (3) получил зависимость $\frac{1}{x}$ от $\frac{1}{n}$, то при построении графика удобнее по горизонтали откладывать обратную величину изменяемой величины, т.е. $\frac{1}{n}$. Очевидно, что на результат такая смена осей не влияет.

Плотность изоленты

Решение