Pho.rs: Не зная броду, не суйся в воду

1 ^?? Проведите измерение величин $a$ и $b$ для разных уровней воды $H$ в стакане.

Проводим измерения, результаты представлены в таблице 1. В последнем столбце указано значение $h$, расчет которого проведён по формуле, полученной в пункте 2.

Ответ:

№ п/п	$H,{~}мм$	$a,{~}мм$	$b,{~}мм$	$x,{~}мм$	$h,{~}мм$
1	45	37	242	2	13,1
2	49	34	242	2	14,2
3	54	31	242	2	15,6
4	58	30	242	2	16,1
5	63	28	242	2	17,3
6	67	26	242	2	18,6
7	71	25	242	2	19,4
8	75	24	242	2	20,2
9	78	23	242	2	21,0
10	81	22	242	2	22,0
11	85	21	242	2	23,0

2 ^?? Используя рисунок, получите расчётную формулу для зависимости $h$ через $a$, $b$ и $x$.

Получим расчётную формулу для $h$. Из подобия треугольников $ABC$ и $ADE$:
$$\frac{h}{x}=\frac{b}{a};\\h=\frac{b\cdot x}{a}.$$
В таблицу 1 добавлен столбец, в котором содержатся результаты расчёта $h$.

Ответ: $h=\frac{b\cdot x}{a}.$

3 ^?? Постройте график зависимости $h$ от $H$ и определите коэффициент $k$ для воды.

Строим график зависимости $h(H)$:

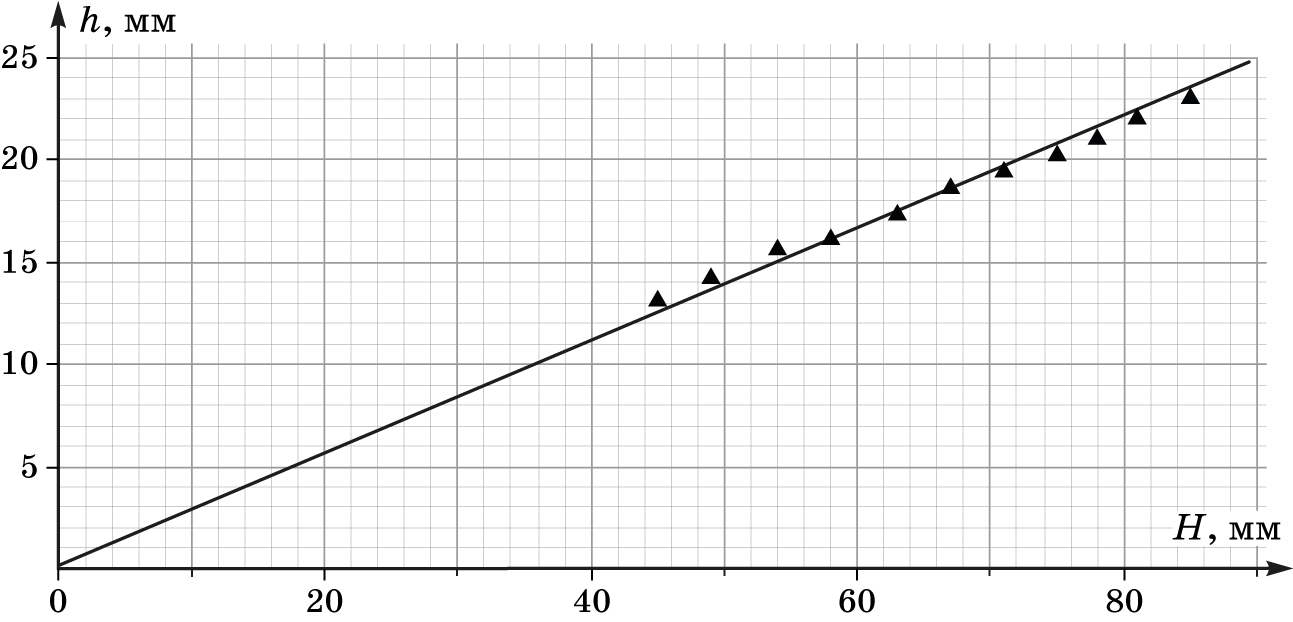
Так как точки хорошо ложатся на прямую, проходящую через начало координат, делаем вывод о линейной зависимости $h$ от $H$.
Проводим прямую через начало координат и определяем угловой коэффициент:
$$k \approx 0,28.$$

Ответ: $k\approx0,28.$

4 ^?? Постройте ход луча из точки $A$ и, используя закон преломления света, теоретически получите формулу для нахождения величины смещения $h$ для слоя воды $H$. Рассмотрите преломление для малых углов падения. Определите показатель преломления $n$ воды, используя свой результат для коэффициента $k$.

Рассмотрим плоскопараллельную пластину (слой воды) толщиной $H$ и показателем преломления $n$. Построим ход двух лучей, идущих от точки $A$, расположенной на нижней поверхности пластины (дне водного слоя). Луч $AK$ падает на верхнюю поверхность перпендикулярно, поэтому выходит без преломления. Угол падения луча $AM$ равен $\varphi$, он выходит из пластины (слоя) под углом $\varphi^\prime$ к перпендикуляру $LM$ к верхней поверхности. Лучи $AK$ и $MN$ попадают наблюдателю «в глаз», и он видит изображение точки $A$ в точке $A^\prime$ (то есть точка $A$ как бы приподнимается с точки зрения наблюдателя).

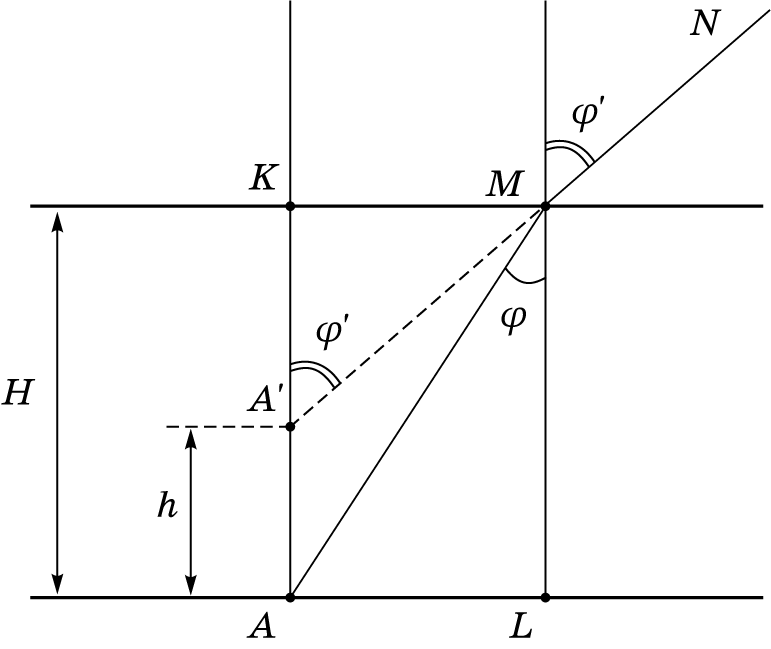
По закону преломления $$n\cdot \sin\varphi=1\cdot \sin\varphi^\prime.$$
Абсолютный показатель преломления воздуха равен 1, показатель преломления воды равен $n$.
Рассмотрим треугольник $ALM$
$$AL=LM\cdot \text{tg}\,\varphi=H\cdot \text{tg}\,\varphi.$$
Запишем соотношение между катетами треугольника $A^\prime KM$
$$KM=KA^\prime\cdot \text{tg}\,\varphi^\prime.$$
Кроме того, $KM=AL$.
Так как угол падения $\varphi$ и угол преломления $\varphi^\prime$ малы, то
$$\text{tg}\,\varphi\approx\sin\varphi\approx\varphi; \\\text{tg}\,\varphi^\prime\approx\sin\varphi^\prime\approx\varphi^\prime.$$
Тогда
$$H\cdot \text{tg}\,\varphi=KA^\prime\cdot\text{tg}\,\varphi^\prime;\\H\cdot \sin\varphi=KA^\prime\cdot n \cdot \sin\varphi;\\H\cdot \varphi=KA^\prime\cdot n \cdot \varphi;$$
Так как
$$KA^\prime=KA-AA^\prime=H-h,$$
то для $h$ получим
$$h=\frac{n-1}{n}\cdot H.$$
Таким образом коэффициент преломления $n$ связан с найденным коэффициентом $k$ соотношением
$$k=\frac{n-1}{n}.$$
Выразим показатель преломления $n$
$$n=\frac{1}{1-k}$$.
Подставим значения, найдем показатель преломления воды в нашей работе
$$n=\frac{1}{1-0,28}=1,39.$$

Ответ: $n=1,39.$

Не зная броду, не суйся в воду

Решение