1  ^?? Определите радиус шарика для пинг-понга $R$. Укажите в работе действия, которые Вы предпринимали для повышения точности результата.

После Олимпийских игр в австралийском Сиднее, прошедших в 2000 году, вес мячика увеличили до $2,7{~}г$, а диаметр – до $40{~}мм$. Изменение характеристик было продиктовано необходимостью увеличить устойчивость шара в полете и снизить темп игры для большей зрелищности. Но в характеристики шариков, продающихся в магазинах, могут отличаться от международных стандартов.

Метод № 1

Для определения радиуса шарика используем два бруска и миллиметровую бумагу. Зажимаем шарик между брусками в разных местах, где можно измерить его диаметр. За параллельностью брусков следим по миллиметровой бумаге. Проводим измерение несколько раз и находим среднее значение диаметра, а затем определяем радиус по формуле: $R = 0,5D_{ср}$.

№ п/п	$D,{~}мм$	$D_{ср}{~}мм$	$R,{~}мм$
1	39	39	19,5
2	39
3	39

Метод № 2

Делаем на шарике отметку карандашом и с помощью линейки прокатываем его, считая обороты. Измеряем путь шарика по поверхности стола и определяем радиус по формуле: $$R = \frac{L_{ср}}{2\pi n}.$$

№ п/п	$n$	$L,{~}мм$	$L_{ср},{~}мм$	$R,{~}мм$
1	3	368	368	19,5
2	3	370
3	3	366

2  ^?? Исследуйте зависимость массы сферического сегмента от его высоты и определите степень $n$ и коэффициент $k$ для выданного Вам сегмента.

Измеряем массу сегмента на весах. Для определения высоты сегмента опять используем два бруска и миллиметровую бумагу. Зажимаем сегмент между брусками. За параллельностью брусков следим по миллиметровой бумаге. Аккуратно срезаем полоску с сегмента ножницами, уменьшая его высоту. Следим за аккуратностью среза на плоскости стола.

№ п/п	1	2	3	4	5	6	7	8	9
$m,{~}г$	1,50	1,41	1,23	1,10	0,96	0,76	0,60	0,48	0,35
$h,{~}мм$	35	33	29	26	22	18	14	11	8

Строим график зависимости массы сегмента от его высоты.

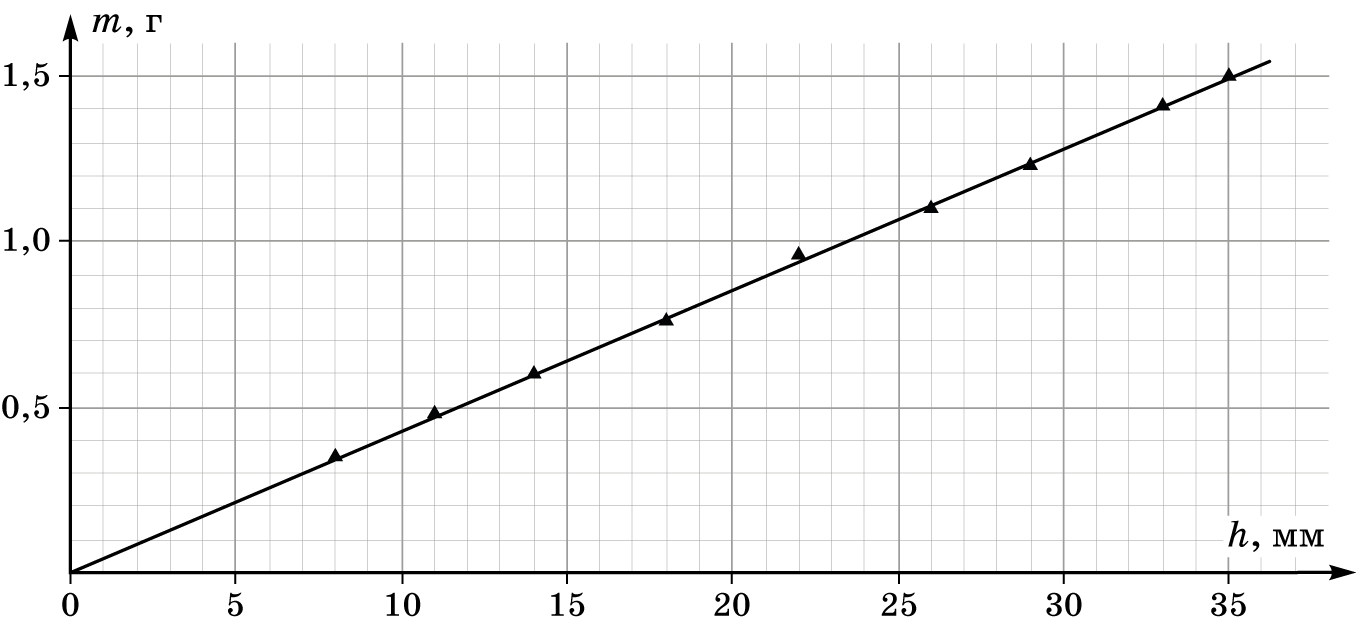
Т.к. точки хорошо ложатся на прямую, проходящую через начало координат, делается вывод о прямой пропорциональности и равенстве $n$ единице. Проводим среднюю прямую через начало координат и определяем угловой коэффициент: $$k = \frac{1,2}{28} = 0,043{~}\frac{г}{мм}$$.

3  ^?? С помощью полученной зависимости определите массу целого шарика для пинг-понга.

Метод № 1

Массу целого шарика можно найти на графике, используя экстраполяцию до диаметра.

Метод № 2

Массу целого шарика можно найти по формуле: $$m_0 = kD = 0,043\cdot 39 = 1,68{~}г.$$

4  ^?? В этой части задания не требуется построения графиков для каких-либо зависимостей. Определите поверхностную и объёмную плотности материала шарика для пинг-понга. Укажите в работе действия, которые Вы предпринимали для повышения точности результатов плотностей.

Поверхностную плотность легко найти по формуле: $$\rho_S=\frac{m_0}{4\pi R^2}=\frac{1,68\cdot 10^{-3} {~}кг}{4\cdot 3,14\cdot \left(19,5\cdot 10^{-3}{~}м \right)^2}\approx 0,35{~}\frac{кг}{м^2}$$ . Для определения объёмной плотности необходимо измерить толщину стенки шарика. Для этого используются обрезки шарика. Они выкладываются в ряд и зажимаются брусками. Толщину стенки определяем методом рядов: $$l_1=\frac{l}{N}$$. Тогда объёмная плотность: $$\rho_V=\frac{m_0}{4\pi R^2l_1}=\frac{m_0N}{4\pi R^2l}=\frac{1,68\cdot 10^{-3} {~}кг\cdot 13}{4\cdot 3,14\cdot \left(19,5\cdot 10^{-3}{~}м \right)^2\cdot5\cdot10^{-3}м }\approx 920{~}\frac{кг}{м^3}.$$