1  ^?? Запишите уравнение динамики для зависимости угла $\theta(t)$ от времени.

В системе отсчёта, связанной с осью $O$, на стержень действует сила инерции:\[F_{\mathrm{in}}=-m\ddot{z}=m\omega^2A\cos\omega t.\]Уравнение моментов, действующих на стержень:\[-(mg-F_{\mathrm{in}})\frac{l}{2}\sin\theta=\frac{1}{3}ml^2\ddot{\theta}\implies\]

2  ^?? Выведите уравнение, которому удовлетворяет $\varphi(t)$.

Представим $\theta=\varphi+\delta$. Поскольку $\delta\ll1$, можно разложить $\sin\theta$ в ряд Тейлора:\[-\Bigl(m g-m\omega^{2}A\cos\omega t\Bigr)\frac{l}{2}(\sin\varphi+\cos\varphi\cdot\delta)=\frac{1}{3}m l^{2}(\ddot{\varphi}+\ddot{\delta})\implies\\-mg\frac{l}{2}\sin\varphi-mg\frac{l}{2}\cos\varphi\cdot\delta+m\omega^2A\cos\omega t\cdot\frac{l}{2}\sin\varphi+m\omega^2A\cos\omega t\cdot\frac{l}{2}\cos\varphi\cdot\delta=\frac{1}{3}ml^2\left(\ddot{\varphi}+\ddot{\delta}\right).\]Усредним полученное уравнение по периоду $\delta$:\[-mg\frac{l}{2}\sin\varphi-mg\frac{l}{2}\cos\varphi\cdot\langle\delta\rangle+m\omega^2A\langle\cos\omega t\rangle\cdot\frac{l}{2}\sin\varphi+m\omega^2A\frac{l}{2}\cos\varphi\cdot\langle\delta\cdot\cos\omega t\rangle=\frac{1}{3}ml^2\left(\ddot{\varphi}+\left\langle\ddot{\delta}\right\rangle\right).\]Поскольку $\langle\delta\rangle=0$, $\langle\cos\omega t\rangle=0$ и $\left\langle\ddot{\delta}\right\rangle=0$:\[-mg\frac{l}{2}\sin\varphi+m\omega^2A\frac{l}{2}\cos\varphi\cdot\langle\delta\cdot\cos\omega t\rangle=\frac{1}{2}ml^2\ddot{\varphi}.\]Чтобы найти $\langle\delta\cdot\cos\omega t\rangle$, помножим исходное уравнение на $\cos\omega t$ и усредним по времени:\[-mg\frac{l}{2}\sin\varphi\cos\omega t-mg\frac{l}{2}\cos\varphi\cdot\delta\cdot\cos\omega t+m\omega^2A\cos^2\omega t\cdot\frac{l}{2}\sin\varphi+m\omega^2A\cos^2\omega t\cdot\frac{l}{2}\cos\varphi\cdot\delta=\frac{1}{3}ml^2\left(\ddot{\varphi}\cos\omega t+\ddot{\delta}\cos\omega t\right).\]Учитывая, что $\ddot{\delta}=-\omega^2\delta$, $\left\langle\cos^2\omega t\right\rangle=\frac{1}{2}$ и $\left\langle\delta\cdot\cos^2\omega t\right\rangle=0$:\[-mg\frac{l}{2}\cos\varphi\cdot\langle\delta\cdot\cos\omega t\rangle+m\omega^2A\frac{l}{2}\sin\varphi\cdot\frac{1}{2}=-\frac{1}{2}ml^2\omega^2\cdot\langle\delta\cdot\cos\omega t\rangle\\\implies \langle\delta\cdot\cos\omega t\rangle=\frac{-\frac{3}{4}A\omega^2\sin\varphi}{l\omega^2-\frac{3}{2}g\cos\varphi}\approx-\frac{3}{4}\frac{A}{l}\sin\varphi\implies\]

3  ^?? Считая, что $V_{\mathrm{eff}}(\varphi=0)=0$, получите выражение для $V_{\mathrm{eff}}(\varphi)$.

Эффективный момент силы, действующий на стержень:\[M(\varphi)=-mg\frac{l}{2}\sin\varphi-\frac{3}{8}m\omega^2A^2\sin\varphi\cos\varphi\equiv-\frac{\mathrm dV_{\mathrm{eff}}(\varphi)}{\mathrm d\varphi}.\]Проинтегрируем $V_{\mathrm{eff}}(\varphi)\equiv\int\limits_{\varphi}^0M(\xi)~\mathrm d\xi$ и получим:

4  ^?? Определите положения равновесия $\varphi_0$ стержня в поле $V_{\mathrm{eff}}(\varphi)$. Исследуйте эти положения равновесия на устойчивость. Найдите частоту малых колебаний относительно устойчивых положений равновесия. Рассмотрите все возможные случаи.

Условие равновесия:\[M(\varphi_0)=\left(\frac{1}{2}mgl+\frac{3}{8}m\omega^2A^2\cos\varphi_0\right)\sin\varphi_0=0\implies\sin\varphi_0=0\implies \]

Если $\omega^2 > \frac{4gl}{3A^2}$, существуют положения равновесия\[\cos\varphi_0=-\frac{4gl}{3\omega^2A^2}\implies\]

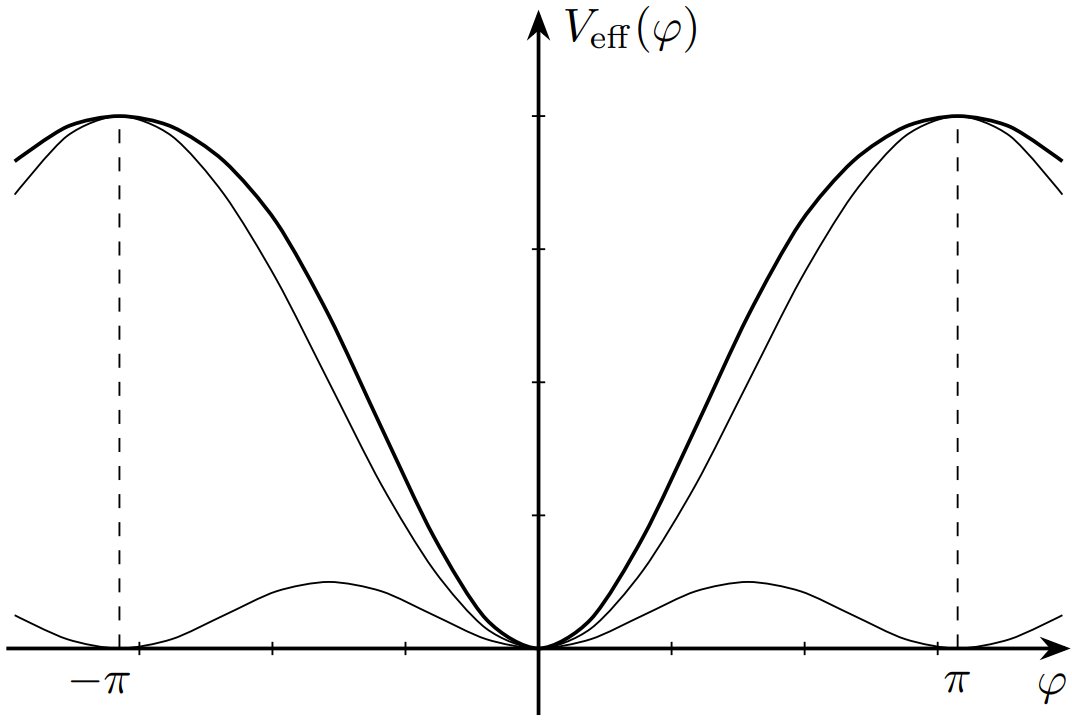
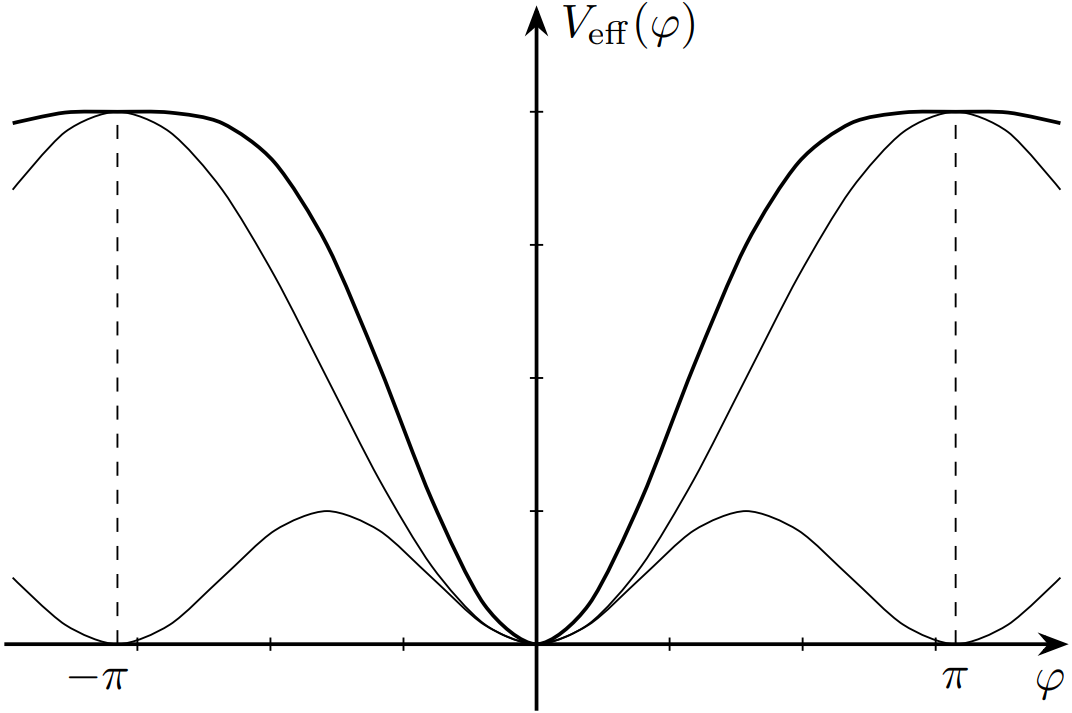
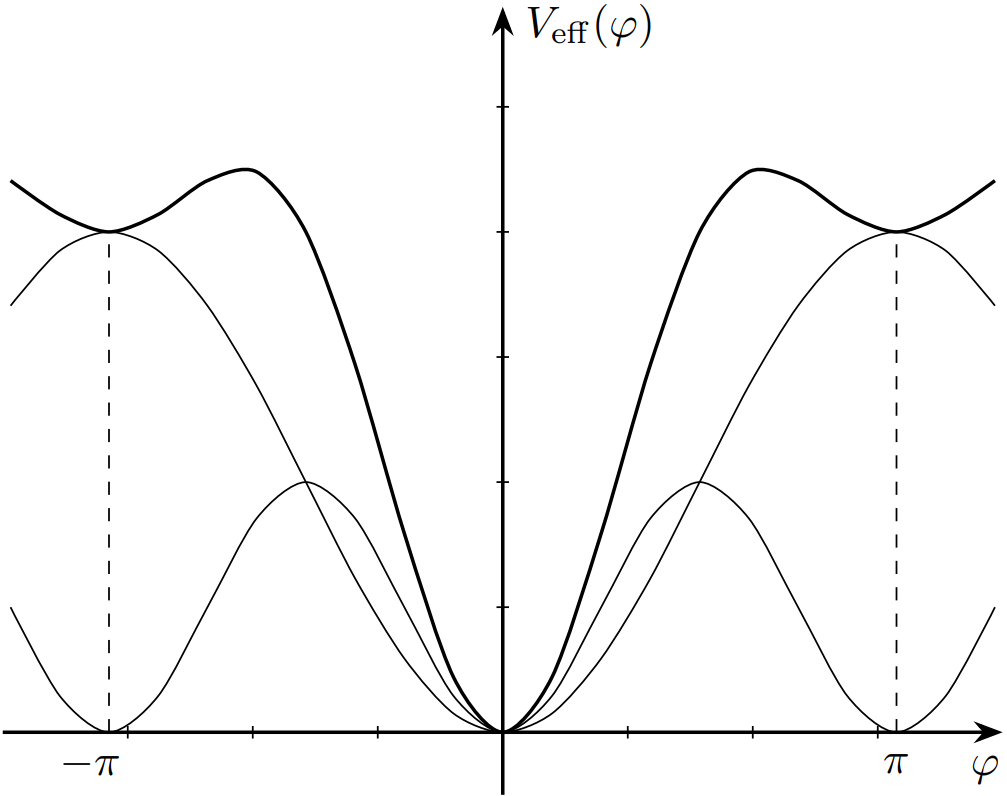
Частота малых колебаний стержня около положения равновесия\[f=\frac{1}{2\pi}\sqrt{\frac{V''_{\mathrm{eff}}(\varphi_0)}{ml^2/3}}\implies\]

5  ^?? Найдите $\omega_c$ и максимальный угол $\varphi_{\max}$, на который может подняться стержень в случае $\omega_0 < \omega_c$. Рассмотрите все возможные случаи.

Начальная кинетическая энергия стержня при $\omega_0=\omega_c$ должна быть равна его максимальной потенциальной энергии в процессе движения.

В случае $\omega^2 \le \frac{4gl}{3A^2}$ кинетическая энергия стержня должна быть равна его потенциальной энергии в точке $\varphi=\pm\pi\implies$\[\frac{1}{2}\frac{1}{3}ml^2\omega_c^2 = V_{\mathrm{eff}}(\varphi=\pi)=mgl\implies\]

В случае $\omega^2 > \frac{4gl}{3A^2}$ кинетическая энергия стержня должна быть равна его потенциальной энергии в точке $\varphi=\pm\pi\mp\arccos\frac{4gl}{3\omega^2A^2}\implies$\[\frac{1}{2}\frac{1}{3}ml^2\omega_c^2 = V_{\mathrm{eff}}\left(\varphi=\pi-\arccos\frac{4gl}{3\omega^2A^2}\right)=\frac{1}{2}mgl+\frac{3}{16}m\omega^2A^2+\frac{mg^2l^2}{3\omega^2A^2}\implies\]

Максимальный угол в случае $\omega_0 < \omega_c$ определяется точкой, в которой:\[\frac{1}{2}\frac{1}{3}ml^2\omega_0^2=V_{\mathrm{eff}}(\varphi_{\max})\implies\cos^2\varphi_{\max}+\frac{8gl}{3\omega^2A^2}\cos\varphi_{\max}+\frac{8\omega_0^2l^2}{9\omega^2A^2}-\frac{8gl}{3\omega^2A^2}-1=0\\\implies\cos\varphi_{\max}=\frac{1}{2}\left[-\frac{8gl}{3\omega^2A^2}\pm\sqrt{\left(\frac{8gl}{3\omega^2A^2}\right)^2-4\left(\frac{8\omega_0^2l^2}{9\omega^2A^2}-\frac{8gl}{3\omega^2A^2}-1\right)}\right].\]Из соображений физического смысла следует выбрать знак $+$. Итого: