Подсказка:\[\int{\frac{\mathrm{d}x}{\sqrt{\left(x^{2}+a^{2}\right)^{3}}}}={\frac{x}{a^{2}{\sqrt{x^{2}+a^{2}}}}}+\operatorname{const}.\]

Как показано на рисунке, введём вектор $\vec r'\equiv -z\hat z$, тогда $\mathrm d\vec m=-g\,\mathrm d\vec r'$. Векторный потенциал задаётся интегралом:\[\vec A=\frac{\mu_0}{4\pi}\displaystyle\int\frac{\left[\mathrm d\vec m\times(\vec r-\vec r')\right]}{\left|\vec r-\vec r'\right|^3}=\frac{\mu_0g}{4\pi}\displaystyle\int\frac{\left[\mathrm d\vec r'\times(\vec r-\vec r')\right]}{\left|\vec r-\vec r'\right|^3}=\\=\hat\varphi\cdot \frac{\mu_0gr\sin\theta}{4\pi}\displaystyle\int\limits_0^{-\infty}\frac{-\mathrm dz}{\sqrt{\left|(z-r\cos\theta)^2+r^2\sin^2\theta\right|^3}}.\]Применяя подсказку, получим:\[\vec A=\hat\varphi\cdot \frac{\mu_0gr\sin\theta}{4\pi}\left.\frac{z-r\cos\theta}{r^2\sin^2\theta\sqrt{(z-r\cos\theta)^2+r^2\sin^2\theta}}\right|^{z=0}_{z=-\infty}=\\=\hat\varphi\cdot \frac{\mu_0gr\sin\theta}{4\pi}\left[\frac{-r\cos\theta}{r^2\sin^2\theta\sqrt{r^2\cos^2\theta+r^2\sin^2\theta}}-\frac{-1}{r^2\sin^2\theta}\right]\implies\]

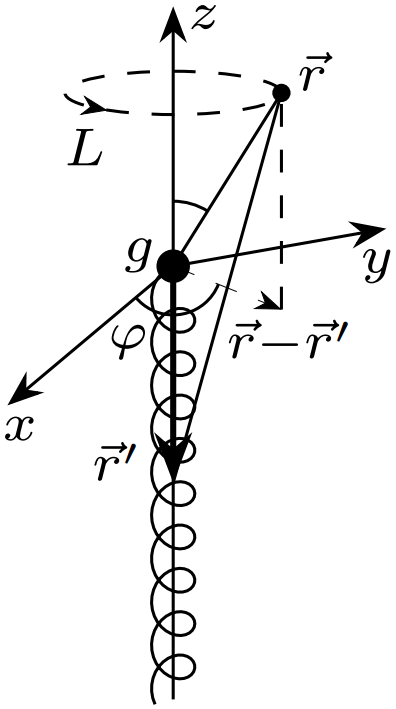
\[\mathrm d\vec l=\hat\varphi\cdot\mathrm dl=\hat\varphi\cdot r\sin\theta\,\mathrm d\varphi\implies \left(\vec A\cdot\mathrm d\vec l\right)=\frac{\mu_0g}{4\pi}(1-\cos\theta)\,\mathrm d\varphi\implies\]

\[\mathrm d\vec S=2\rho\,\mathrm d\rho\cdot\hat z\implies\mathrm d\Phi=2\rho\,\mathrm d\rho\cdot\frac{\mu_0}{4\pi}\frac{g}{|\vec r|^3}\left(\vec r\cdot\hat z\right)=\frac{\mu_0g}{2}\frac{\rho\,\mathrm d\rho}{\left(\rho^2+r^2\cos^2\theta\right)^{3/2}}r\sin\theta\implies\\\implies\Phi_L=\frac{\mu_0g}{2}r\cos\theta\int\limits_0^{r\sin\theta}\frac{\rho\,\mathrm d\rho}{\left(\rho^2+r^2\cos^2\theta\right)^{3/2}}=-\frac{\mu_0g}{2}r\cos\theta\left.\frac{1}{\sqrt{\rho^2+r^2\cos^2\theta}}\right|_0^{r\sin\theta}\implies\]

Подсказка: удобно рассматривать струну Дирака как тонкий соленоид.

\[g=\frac{\mathrm dm}{\mathrm dl}=\frac{SI(t)\cdot n\,\mathrm dl}{\mathrm dl}\implies\]

Подсказка: рассмотрите телесный угол, под которым треугольник виден из начала координат.

Телесный угол, под которым треугольник виден из начала координат, найти несложно. Заметим, что треугольник находится на том же расстоянии от начала координат, на котором грань тетраэдра с ребром $a$ находится от центра этого тетраэдра. Значит\[\Omega_\Delta=\frac{4\pi}{4}=\pi.\]Тогда поток, создаваемый магнитным зарядом, будет равен\[\Phi_1=-\frac{1}{4}\mu_0g.\]Поток внутри соленоида при этом равен\[\Phi_0=\mu_0g\implies\Phi=\Phi_0+\Phi_1=\frac{3}{4}\mu_0g.\]ЭДС, создаваемая в треугольнике:\[\mathcal E=-\dot\Phi=\frac{3}{4}\mu_0nSI_0\omega\sin\omega t.\]Полное сопротивление треугольника $3aR_0\implies$\[W_R=\frac{1}{3aR_0}\overline{\mathcal E^2(t)}=\frac{1}{3aR_0}\left(\frac{3}{4}\mu_0nSI_0\omega\right)^2\cdot \overline{\sin^2\omega t}\quad\overset{\overline{\sin^2\omega t}=1/2}\implies\]

Пусть разность фаз интерферирующих волновых функций в некоторой точке экрана до включения тока равна $\Delta\phi_0$. Тогда после включения тока:\[\Delta\phi_1=\int\limits_{C_1}\left(\vec k\cdot\mathrm d\vec l\right)-\int\limits_{C_2}\left(\vec k\cdot\mathrm d\vec l\right)=\frac{1}{\hbar}\left[\int\limits_{C_1}\left(\vec p\cdot\mathrm d\vec l\right)-\int\limits_{C_2}\left(\vec p\cdot\mathrm d\vec l\right)\right]-\frac e\hbar\left[\int\limits_{C_1}\left(\vec A\cdot\mathrm d\vec l\right)+\int\limits_{-C_2}\left(\vec A\cdot\mathrm d\vec l\right)\right]=\Delta\phi_0-\frac e\hbar\oint\limits_C\left(\vec A\cdot\mathrm d\vec l\right),\]где $C_1$ и $C_2$ -- пути от каждой из щелей до экрана, а $C$ -- контур вокруг соленоида. Поскольку циркуляция векторного потенциала по контуру равна потоку через него, то включение тока приводит к дополнительной разности фаз:\[\Delta\phi=\Delta\phi_1-\Delta\phi_0=-\frac e\hbar\Phi=-\frac e\hbar\mu_0nIS.\]Смещение вдоль экрана на $x$ приводит к изменению разности фаз на:\[\Delta\phi_x\approx k_0d\theta=\frac p\hbar\cdot d\cdot\frac xD.\]Наконец, смещение главного максимума определяется соотношением:\[\Delta\phi_x+\Delta\phi=0\implies \frac{pd}{\hbar D}\Delta x-\frac e\hbar\mu_0nIS=0\implies\]