$!Важно:$ прежде чем менять конфигурацию схемы, плавно выкрутите амплитуду генератора в ноль, после чего выключите генератор и источник тока! Новые катушки выдаваться не будут!

Часть А. Колебательный контур с нелинейной ёмкостью.

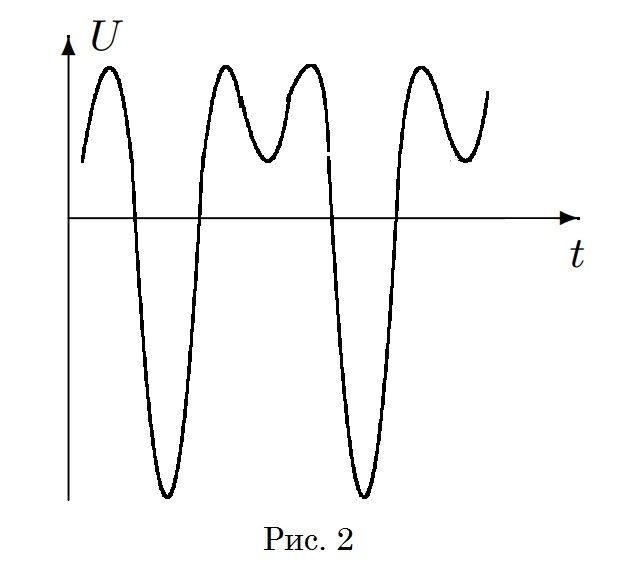
\emph{Оборудование, используемое в этой части:} генератор, источник постоянного напряжения, осциллограф, мультиметр, набор проводов для приборов, макетная плата, набор проводов для платы, варикап, резистор $R_0=1~МОм$ (бежевый цвет), резистор $r=10~Ом$ (синий цвет), три катушка индуктивности $L_1=3,3~мГн, L_2=15,0~мГн, L_3=15,0~мГн$, конденсатор $C_{ш}=10~мкФ$ (маркировка 105).

В первой части работы изучаются резонансные свойства нелинейного колебательного контура. В качестве нелинейного элемента, входящего в состав колебательного контура, используется полупроводниковый диод (варикап), ёмкость которого зависит от величины постоянного напряжения на нем.

В произвольный момент времени напряжение на варикапе $U=U_\sim + V$, где $U_\sim-$ переменная составляющая напряжения, а $V-$ постоянная составляющая напряжения.
Пусть на варикапе $C$ поддерживается постоянное напряжение $V=-V_0$, тогда зависимость ёмкости варикапа от напряжения на нем в окрестности рабочей точки можно записать в виде:
$$
C(V)=C_0+\chi(V+V_0)+\beta(V+V_0)^2
$$

Соберите установку (рис. 1). В этой части используйте только катушку $L_1$. Обратите внимание на полярность включение варикапа! Белая точка подключается к плюсу источника.

A1  ^1.20 Установите амплитуду напряжения на генераторе $\mathcal{E}_0 < 1,0~B$. Снимите зависимость резонансной частоты $f_{рез}$ контура от величины постоянного напряжения на варикапе $V_{0}$ в диапазоне от $0$ до $3~В$.

A2  ^0.90 Постройте график зависимости ёмкости cхемы от приложенного к нему напряжения $C(V+V_0)$. Определите параметры $\chi$ и $\beta$.

A3  ^1.00 Снимите резонансную кривую для $V_0=0,3~B$. По полученной зависимости определите добротность контура $Q$.

A4  ^0.40 Теоретически вычислите добротность контура через его параметры (не используя резонансную кривую).

Часть В. Эффект удвоения частоты.

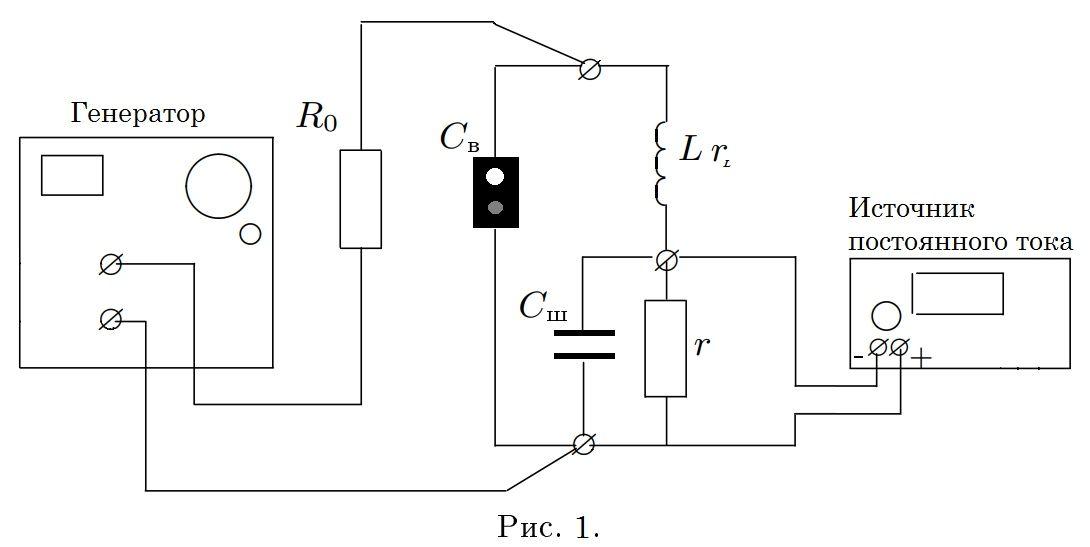
Из-за того, что ёмкость контура зависит от напряжения, при некоторых условиях частота колебаний в нем может не совпадать с частотой генератора. В частности при частоте генератора $\omega = \frac{\omega_0}{2}$ возникают колебания с собственной частотой $\omega_0$.

Используя уравнения Кирхгофа и некоторые разложения в окрестности рабочей точки можно получить уравнение колебаний переменной составляющей напряжения на варикапе в виде:
$$
\ddot{U}+2\gamma\dot{U}+\omega_0^2U=-\omega_0^2U_0sin(\omega t)+\alpha' U^2
$$
где введены обозначения $U_0=\cfrac{L\omega_0}{R_0}\mathcal{E}_0,~\alpha'=2\omega_0^2 \cfrac{\chi-\beta V_0}{C_0-\chi V_0}$.

B1  ^0.60 Выразите $\gamma$ и $\omega_0$ через $r, r_L, C_k, L$.

B2  ^0.90 Пусть частота колебаний внешнего напряжения $\omega=\cfrac{\omega_0}{2}$. Найдите решение уравнения колебаний переменной составляющей напряжения на варикапе $U_1$ в первом(линейном) приближении при слабом затухании $(\gamma \ll \omega_0)$.

B3  ^0.60 При учете нелинейных членов(во втором приближение) решение уравнения колебаний переменной составляющей напряжения на варикапе представляет суперпозицию $U=U_1+U_2$. Получите уравнение колебаний для $U_2$ в терминах $\alpha', \gamma, \omega_o, U_0 $.

B4  ^0.90 Считая, что $U_1 \gg U_2 $ найдите из полученного в пункте В3 уравнения поправку $U_2$ к напряжению на варикапе.

При частоте генератора $\frac{\omega_0}{2}$ сигнал будет иметь вид как на рисунке 2.

B5  ^1.00 Установите частоту генератора $\omega = \frac{\omega_0}{2}$. Снимите экспериментальную зависимость амплитуды $A_2$ колебаний с частотой $\omega_0$ от индуктивности в цепи.

B6  ^0.60 Пусть $A_2 \propto L^\xi$. Из теоретической формулы для $A_2$ получите значение $\xi$.

B7  ^1.00 Найдите значение $\xi$ по измеренной зависимости $A_2(L)$

B8  ^0.90 Установите на варикапе $V_0=0,3~В$, амплитуду генератора $\mathcal{E}_0=12~В.$ Зарисуйте зависимости переменного напряжения на варикапе от времени для $\omega=\frac{\omega_0}{n}$ для $n=3,4,5$.