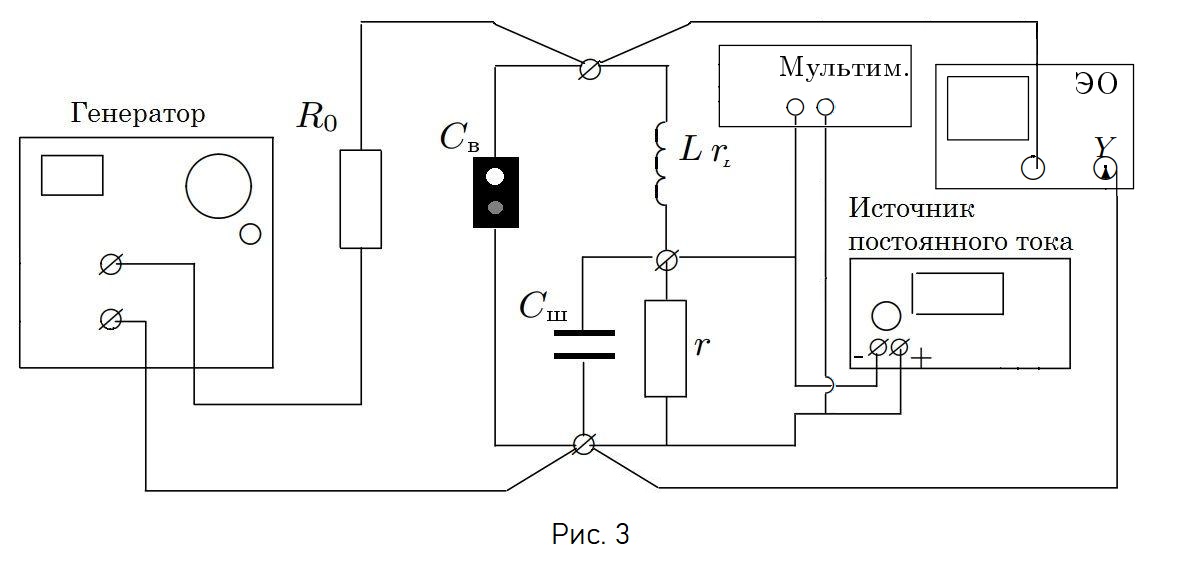
Собираем установку (рис. 1). Устанавливаем напряжение на генераторе $\mathcal{E}_0 = 0,9~B$. Подключаем осциллограф и источник постоянного напряжения, мультиметр для измерения $V_0$ (рис.3). Меняя частоту входного напряжения, находим резонансную частоту контура по максимуму напряжения на варикапе, для фиксированного значение $V_0$.

По формуле резонансной частоты колебательного контура $C=\cfrac{1}{(2\pi f)^2 L } $ пересчитываем зависимость $C(V_0)$.

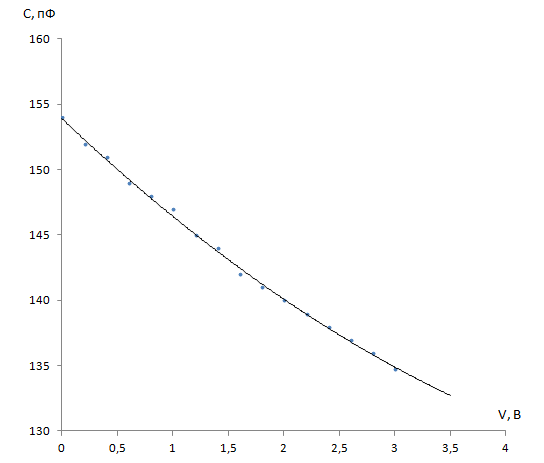
Из касательной графика в нуле находим $\chi $
$$\chi = (4 - 9 )\cdot10^{-12} \cfrac{\text{Ф}}{\text{В}}$$

Из касательных графика в точках $V_0= 0,0 \text{ B}$ и $ V_0 =2,8 \text{ B}$: $$ \beta=\cfrac{C'(2,8)-C'(0,0)}{2 *2,8} $$

$$\beta \sim 10^{-12} \div 10^{-13} \cfrac{\text{Ф}}{\text{В}^2}$$

Устанавливаем напряжение на источнике постоянного напряжения $V_0=0,3 \text{ B}$. Снимаем с осциллографа зависимость $U_{\sim} (f)$.

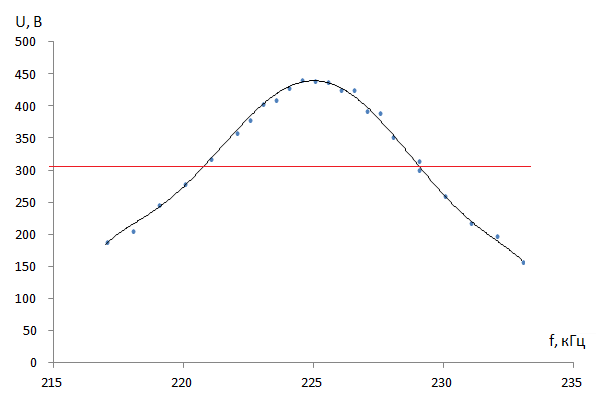
Из полученного графика находим ширину контура по напряжению $U_{\sim}=\cfrac{U_{\sim,max}}{\sqrt2}$ :
$$\delta f = 8 \text{ кГц}$$
$$ Q=\cfrac{f_0}{\delta f} = 28 $$

Из графика пункта А2 находим $C_k(0,3)= 151,7 \text{ пФ}$.
Измеряем мультиметром $r+r_L=33 \text{ Ом} $
$$Q=\cfrac{1}{r+r_L} \sqrt{\cfrac{L}{C_k(0,3)}}=140$$

$$\gamma = \cfrac{r+r_L}{2L}$$

$$\omega_0 = \sqrt{ \cfrac{1}{L C_k} }$$

В первом(линейном) приближении при слабом затухании $(\gamma \ll \omega_0)$ пренебрегаем членами $\alpha' U^2$ и $ 2\gamma\dot{U}$ . Получаем уравнение:
$$
\ddot{U}+\omega_0^2U=-\omega_0^2U_0sin(\cfrac{\omega_0}{2} t)
$$

Решаем полученное уравнение:
$$
U_1=-\cfrac{4}{3} U_0 sin\left( \cfrac{\omega_0 t}{2} \right)
$$

Подставляем в исходное уравнение $U=U_1+U_2$:
$$
\ddot{U_2}+2\gamma\dot{U_2}+\omega_0^2U_2+\omega_0^2U_0sin(\omega t) - \alpha' U_2^2=\alpha' U_1^2 +2 \alpha' U_1 U_2
$$

Подставляем найденное первое приближение $ U_1=-\cfrac{4}{3} U_0 sin\left( \cfrac{\omega_0 t}{2} \right)$:
$$
\ddot{U_2}+2\gamma\dot{U_2}+\omega_0^2U_2 - \alpha' U_2^2 = \cfrac{8\alpha'}{9} U_0^2 - \cfrac{8\alpha'}{9} U_0^2 cos(\omega_0 t) -\cfrac{8\alpha'}{3} U_0 U_2 sin\left( \cfrac{\omega_0 t}{2} \right)
$$

Пренебрегаем $2 \alpha' U_1 U_2$ по сравнению с $\alpha' U_1^2$ получаем:
$$
\ddot{U_2}+2\gamma\dot{U_2}+\omega_0^2U_2 - \alpha' U_2^2 = \cfrac{8\alpha'}{9} U_0^2 - \cfrac{8\alpha'}{9} U_0^2 cos(\omega_0 t)
$$

Ищем решение в виде $ U_2 = A +B sin(\omega_0 t)$. Получаем конечное выражение для поправки $U_2= - \cfrac{8\alpha'}{9 \omega_0^2} U_0^2 - \cfrac{4\alpha'}{9 \gamma \omega_0} U_0^2 sin(\omega_0 t)$.

Cобираем схему (рис. 3). Находим резонансную частоту $\omega_0$ контура по максимуму колебаний напряжения на варикапе. Устанавливаем частоту генератора $\omega = \frac{\omega_0}{2}$. Снимаем зависимость амплитуды $A_2$ колебаний с частотой $\omega_0$ от индуктивности в цепи.

$$A_2=\cfrac{U_{max}-U_{min}}{2}$$

Из пункта B4: $$U_2= - \cfrac{8\alpha'}{9 \omega_0^2} U_0^2 - \cfrac{4\alpha'}{9 \gamma \omega_0} U_0^2 sin(\omega_0 t)$$
$$\alpha' \sim \cfrac{1}{L} $$
$$ U_0^2 \sim L$$
$$ \omega_0 \sim \cfrac{1}{\sqrt{L}}$$
$$ \gamma \sim \cfrac{r+r_L}{L} $$

$$
U_2 \sim L^{\left(\cfrac{3}{2}\right)}
$$
$$ \xi = \cfrac{3}{2}$$

Из пункта B6 видно, что амплитуда колебаний $A_2$ зависит от $L$ и $r_L$ параметров катушки включенной в цепь. Измеряем мультиметром $r+r_L$ для различных значений $L$. Строим график $ \text{ln } (A_2 (r+r_L))$ от $\text{ln } L$.

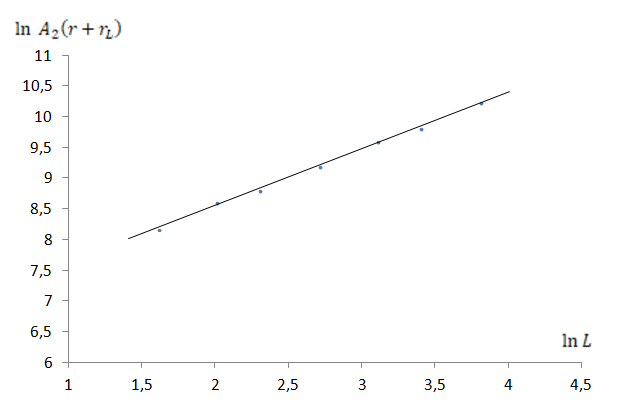
Из коэффициента наклона графика получаем $\xi= 0,9$.