В данном эксперименте электрический чёрный ящик представляет собой плоский конденсатор. Каждая пластина состоит из ряда небольших зубцов одинаковой геометрической формы. Величину емкости $C$ можно изменять, перемещая в горизонтальном направлении верхнюю пластину относительно нижней. Между пластинами конденсатора находится слой диэлектрика.

Оборудование

Два черных ящика ($A$ и $B$), осциллограф, генератор, макетная плата, соединительные провода и перемычки, конденсаторы $100\,пФ$ (маркировка 101) и $330\,пФ$ (маркировка 331), конденсатор неизвестной емкости $C_1$ (в красной изоляции), катушка индуктивности $15.0\,мГн$ (черный цилиндр с маркировкой 153), резистор $510\,Ом$ (в черной изоляции).

$!Важно!$ Избегайте больших напряжений и резких скачков тока и напряжения. Прежде чем менять конфигурацию схемы, плавно выкрутите амплитуду генератора в ноль, после чего выключите генератор! Новые компоненты выдаваться не будут!

Часть А. Калибровка (1.3 балла)

А1  ^1.00 Соберите колебательный $RLC$-контур, последовательно соединив индуктивность, известную ёмкость и резистор. Измерьте зависимость резонансной частоты этого контура от используемой емкости. Проверьте применимость теоретической связи между ними. Оцените $C_0$ - неустранимую емкость проводов и прочих составляющих схемы.

A2  ^0.30 Соберите колебательный $RLC$-контур, используя конденсатор неизвестной емкости $C_1$. Найдите резонансную частоту этого контура $f_1$. Определите $C_1$.

Часть B. Определение формы пластин конденсаторов (7.2 балла)

Ниже приведены четыре возможные формы пластин.

B1  ^1.60 Для каждой формы пластин постройте качественный график ожидаемой зависимости $C$ от положения верхней пластины  $x$.

B2  ^2.40 Собрав колебательный $RLC$-контур, снимите зависимость $f(x)$ резонансной частоты от положения верхней пластины. Выполните эти измерения для обоих черных ящиков.

B3  ^1.20 Рассчитайте $C(x)$ для каждого из ящиков. Постройте графики этих зависимостей на одной миллиметровке. Определите номера форм пластин, соответствующих ящикам.

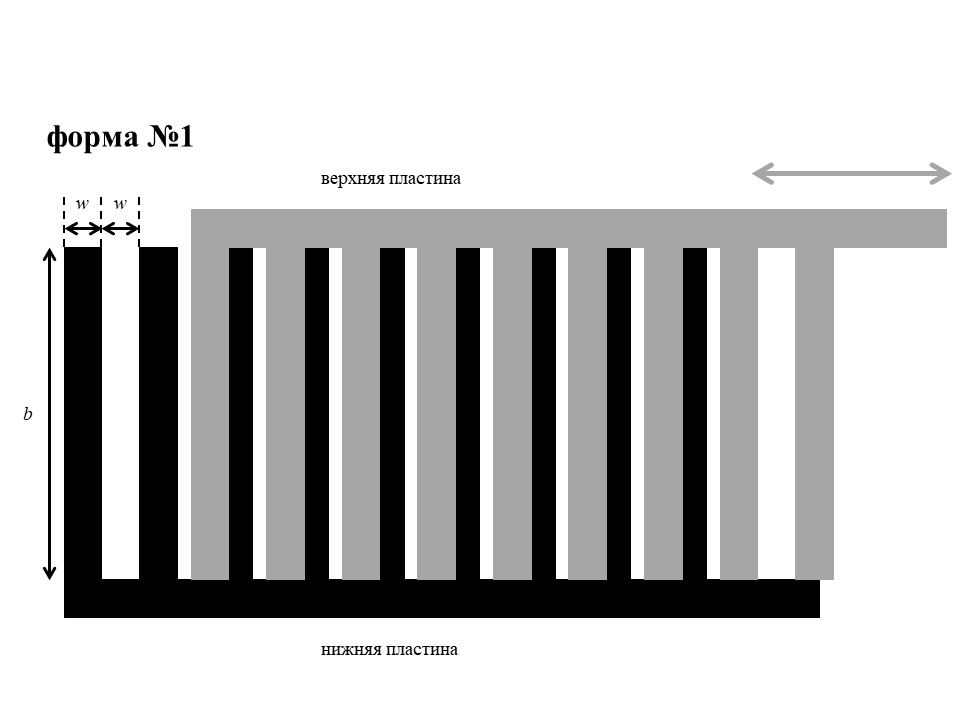
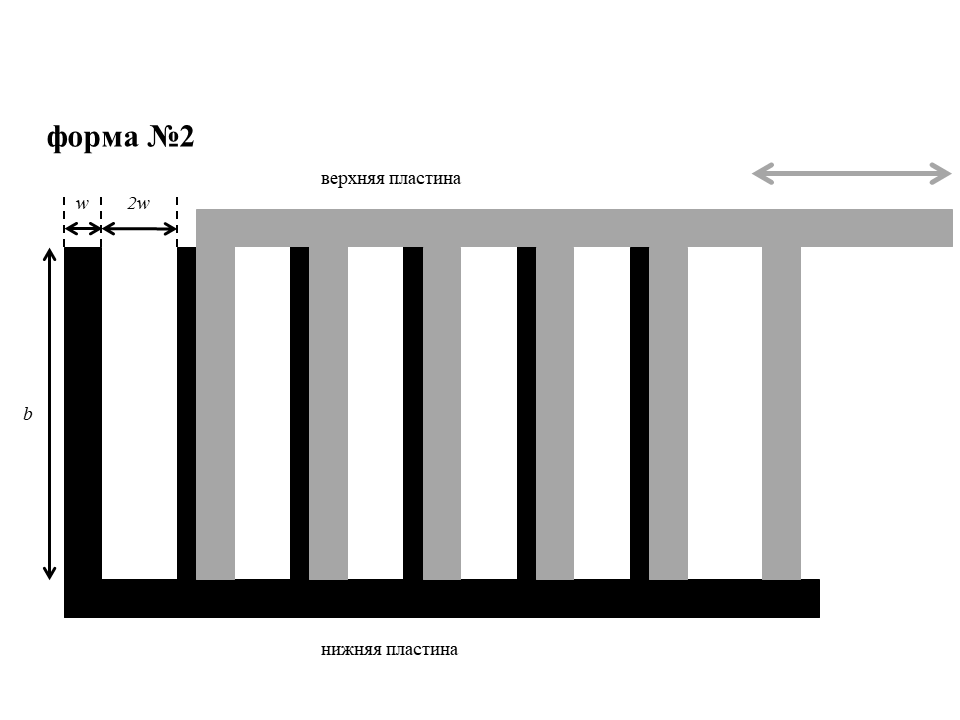
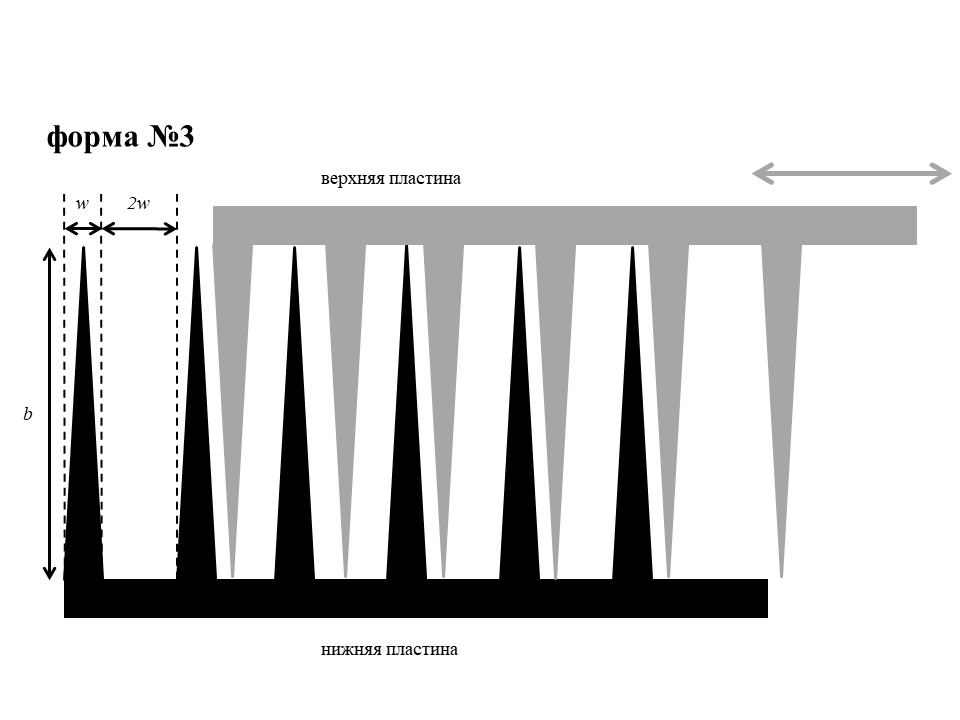
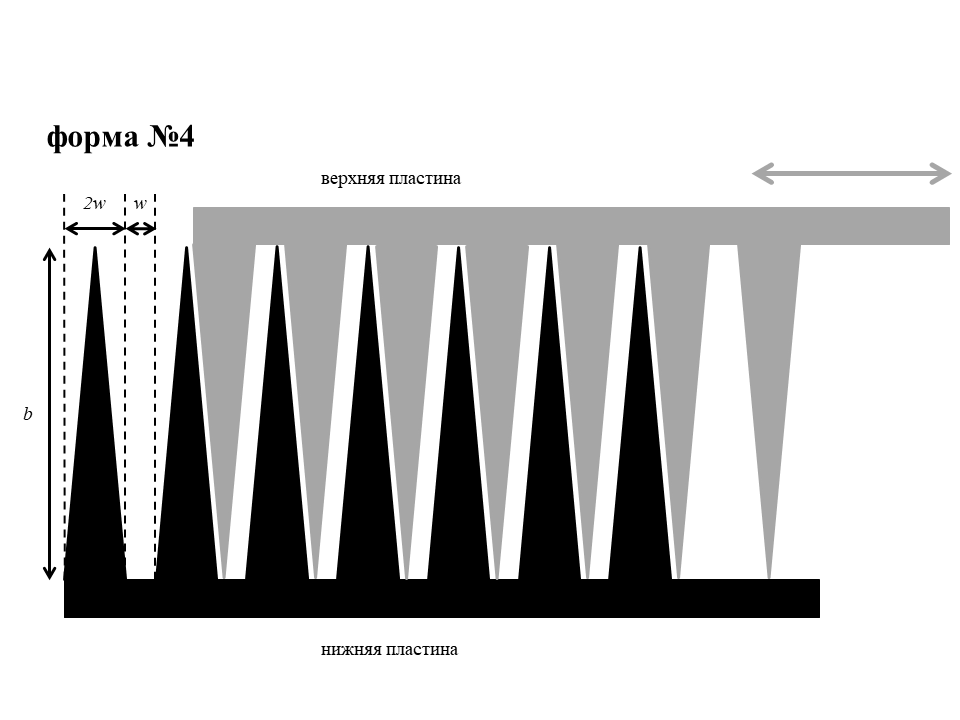
B4  ^1.40 Для каждого из ящиков определите значения $b$ и $w$, характеризующие форму зубцов. Расстояние $d$ между верхней и нижней пластинами составляет $1.00~\text{мм}$. Диэлектрик, находящийся между пластинами, имеет диэлектрическую проницаемость $\varepsilon=2.9$. Электрическая постоянная $\varepsilon_0=8.85\cdot 10^{-12}~\text{Ф/м}$.

B5  ^0.60 Для каждого из ящиков оцените количество зубцов на одной пластине плоского конденсатора. (В каждом ящике количество зубцов на нижней пластине такое же, как на верхней).

Часть C. Разрешающая способность цифрового измерителя перемещений (1.5 балла)

При относительном смещении параллельных пластин емкость плоского конденсатора периодически изменяется, а с ней и резонансная частота контура. Данная установка может быть использована как цифровой измеритель перемещений.

C1  ^1.50 Пусть наш черный ящик с маркировкой $A$ является измерителем перемещений. Для частоты в окрестности $f=120~\text{кГц}$, используя данные эксперимента из части B, оцените разрешающую способность установки: минимальное расстояние $\Delta x$, которое можно измерить. Оценка погрешности окончательного результата не требуется.