A1  ^0.30 Кривизной плоской кривой $\rho$ называется величина, обратная радиусу кривизны траектории. Она может быть найдена следующим образом:
$$\rho=\frac{d\theta}{dl}
$$
где $dl$ — элемент длины кривой, а $d\theta$ — угол поворота касательной к кривой.
Выразите кривизну траектории луча $\rho$ через $r$, $\alpha$ и $\displaystyle\frac{d\alpha}{dr}$.

Траектория луча будет плоской. Если $\alpha$ - угол между вектором скорости луча и линией $OA$, а $\varphi$- угол поворота линии $OA$:
$$\tan\alpha=\frac{rd\varphi}{dr}
$$
По определению кривизна равна
$$\rho=\frac{d\theta}{dl}
$$
где $dl$ - элемент длины траектории, а $d\theta$ - угол поворота касательной к ней.
Выражения для $dl$ и $d\theta$ следующие:
$$dl=\frac{dr}{\cos\alpha} \quad\quad\quad d\theta=d\alpha+d\varphi
$$
Тогда
$$\rho=\cos\alpha\left(\frac{d\alpha}{dr}+\frac{d\varphi}{dr}\right)
$$
Выражая:

A2  ^1.00 Рассмотрим произвольную траекторию луча. Пусть при ${OA}_0=r_0$ показатель преломления $n(r_0)=n_0$, а угол $\alpha(r_0)=\alpha_0$.
Выразите кривизну траектории луча при $OA=r$ через $n_0$, $r_0$, $\alpha_0$, $r$, $n(r)$ и $\displaystyle\frac{dn(r)}{dr}$.

Докажем, что для любой траектории луча в сферически симметричной среде выполняется
$$nr\sin\alpha=const=n_0r_0\sin\alpha_0
$$
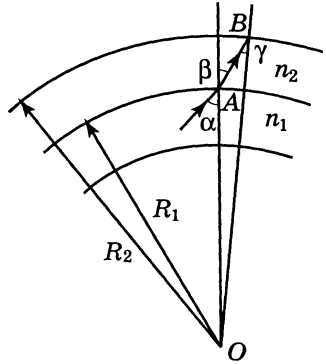
Рассмотрим два тонких сферических слоя, радиусы которых $R_1$ и $R_2$. показатель преломления среды при $R\leq{R_1}$ равен $n_1$, а при $R_1\leq{R}\leq{R_2}$ - $n_2$.
Пусть $\alpha$ и $\beta$ - углы падения и преломления на сфере радиуса $R_1$. Из Закона Снэлла для преломления получим:
$$n_1\sin\alpha=n_2\sin\beta
$$
Пусть $\gamma$ - угол падения на сфере радиуса $R_2$. Из теоремы синусов находим:
$$\displaystyle\frac{R_1}{\sin\gamma}=\displaystyle\frac{R_2}{\sin\beta}
$$
Исключим $\sin\beta$, получим:
$$n_1R_1\sin\alpha=n_2R_2\sin\gamma
$$
что и доказывает инвариантность величины $nr\sin\alpha$.

Отсюда находим:
$$\frac{d\sin\alpha}{dr}=-\frac{n_0r_0\sin\alpha_0}{n^2r^2}\left(n+r\frac{dn}{dr}\right)\qquad\frac{\sin\alpha}{r}=\frac{n_0r_0\sin\alpha_0}{nr^2}
$$
Подставляя в выражение для кривизны:

A3  ^0.40 Используя результат пункта $\textbf{A2}$ , покажите, что кривизна траектории любого луча постоянна при условии:
$$n(r)=\frac{n_1}{1+\left(\displaystyle\frac{r}{a}\right)^2}
$$
где $n_1$ и $a$ — некоторые положительные постоянные.
Во всех остальных пунктах части $\textbf{A}$ эти постоянные считаются известными.
Выразите кривизну траектории луча $\rho$ через, $a$, $r_0$ и $\alpha_0$.

$\textit{Примечание:}$ полученные далее результаты могут быть найдены и прямой подстановкой выражения $n(r)$ в дифференциальное уравнение для $\rho$.

Если траектория луча имеет постоянную кривизну, переменные разделяются:
$$\int\frac{dn}{n^2}=-\frac{\rho}{n_0r_0\sin\alpha_0}\int rdr
$$
Откуда
$$\frac{1}{n}=\frac{\rho r^2}{2n_0r_0\sin\alpha_0}+C
$$
где $C$ - некоторая постоянная интегрирования, определяемая из начальных условий:
$$\displaystyle\frac{1}{n_0}-\displaystyle\frac{\rho r_0}{2n_0\sin\alpha_0}=C
$$
Как видно, данная в условии задачи зависимость является решением полученного уравнения.
Отсюда:

A4  ^0.20 Чему равна максимально возможная кривизна траектории луча $\rho_{max}$ при произвольных значениях $r_0$ и $\alpha_0$?
Ответ выразите через $a$.

Максимум, во-первых, достигается при $\sin\alpha_0=1$, а во-вторых - при $r_0=a$.
Отсюда:

A5  ^0.80 Покажите, что траектории всех лучей, испущенных из точки $A$, находящейся на расстоянии $r_0$ от точки $O$, действительно проходят через одну общую точку $B$.
Найдите также величину расстояния $AB=L$. Ответ выразите через $r_0$ и $a$.

Так как $\rho\sim\sin\alpha_0$, центры всех окружностей лежат на прямой, перпендикулярной $OA$, при этом расстояние от этой прямой до точки $A$ равно $l=\displaystyle\frac{r^2_0+a^2}{2r_0}$.

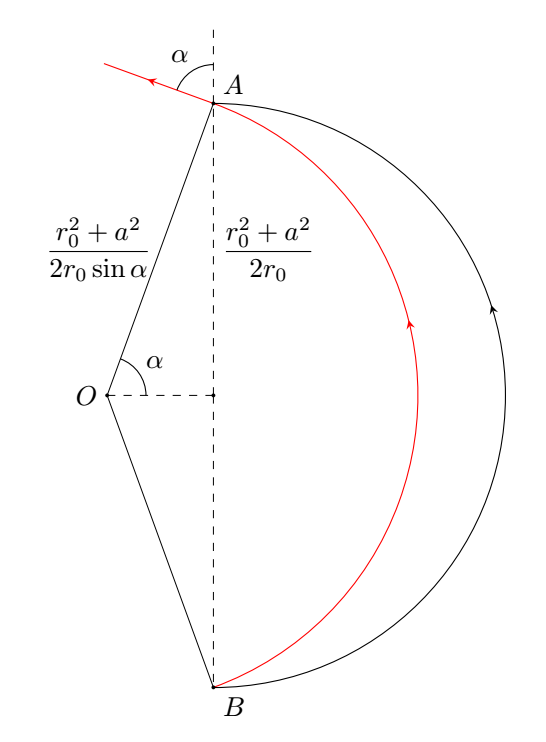
Любые две окружности если пересекаются, то в двух точках. Тогда в силу симметрии вторая точка пересечения $B$ для всех окружностей будет общей и находится от точки $A$ на расстоянии $AB$, равном:

A6  ^0.80 Из принципа Ферма следует, что время движения всех лучей от точки $A$ до точки $B$ одинаково.
Найдите время $T$ после вспышки лучей, через которое произойдёт их фокусировка.
Ответ выразите через $n_1$, $r_0$, $a$ и скорость света в вакууме $c$.
$\textit{Примечание:}$ вам может понадобиться следующий интеграл:
$$\int\frac{dx}{1+k\cos x}=\frac{2}{\sqrt{1-k^2}}\arctan\left(\sqrt{\frac{1-k}{1+k}}\tan\frac{x}{2}\right)+C\quad\text{при}\quad -1<{k}<1
$$

$$\textbf{Первый способ}
$$
Наиболее простой подход - рассмотреть луч, идущий вдоль линии $OA$. Движение будет прямолинейным, тогда:
$$T=\int\limits_0^{r_0}\frac{ndr}{c}+\int\limits_0^{\frac{a^2}{r_0}}\frac{ndr}{c}
$$
Подставляя зависимость $n(r)$ и вводя замену переменной $t=\displaystyle\frac{r}{a}$:
$$T=\frac{n_1 a}{c}\left(\int\limits_0^{\frac{r_0}{a}}\frac{dt}{1+t^2}+\int\limits_0^{\frac{a}{r_0}}\frac{dt}{1+t^2}\right)=\frac{n_1a}{c}\left(\arctan\frac{r_0}{a}+\arctan\frac{a}{r_0}\right)
$$
Таким образом, от $r_0$ время не зависит.
$$\textbf{Второй способ}
$$
Этот же результат можно получить, явно рассматривая движение по окружности. Рассмотрим ту, для которой $\alpha_0=\frac{\pi}{2}$.
Пусть $\beta$ - угловое перемещение луча по окружности от начального положения. Тогда для $r^2$ из теоремы косинусов имеем:
$$r^2=\left(\frac{a^2+r^2_0}{2r_0}\right)^2+\left(\frac{a^2-r^2_0}{2r_0}\right)^2-2\left(\frac{a^2+r^2_0}{2r_0}\right)\left(\frac{a^2-r^2_0}{2r_0}\right)\cos\beta
$$
Перепишем чуть компактнее:
$$r^2=\frac{a^4+r^4_0}{2r^2_0}-\frac{a^4-r^4_0}{2r^2_0}\cos\beta
$$
Для промежутка времени имеем:
$$dT=\frac{nd\beta}{c\rho}=\frac{a^2r_0n_1}{c(a^2+r^2_0)}\frac{d\beta}{1-\frac{a^2-r^2_0}{a^2+r^2_0}\cos\beta}
$$
откуда
$$T=\frac{nd\beta}{c\rho}=\frac{a^2r_0n_1}{c(a^2+r^2_0)}\int\limits_0^{\pi}\frac{d\beta}{1-\frac{a^2-r^2_0}{a^2+r^2_0}\cos\beta}=\frac{\pi a^2r_0n_1}{c(a^2+r^2_0)\sqrt{1-\left(\frac{a^2-r^2_0}{a^2+r^2_0}\right)^2}}
$$

B1  ^1.20 Найдите радиус «Рыбьего глаза» $R$.

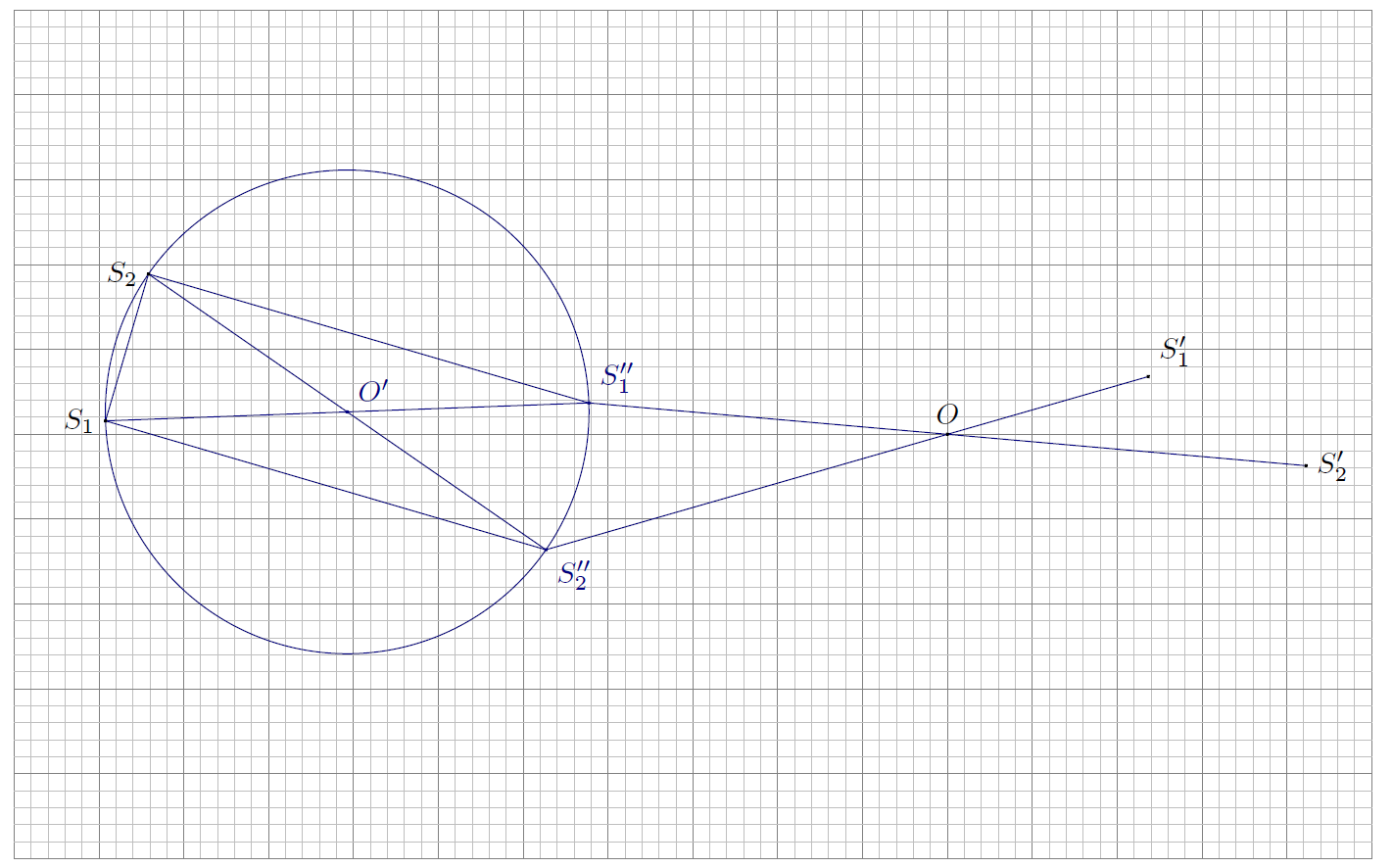
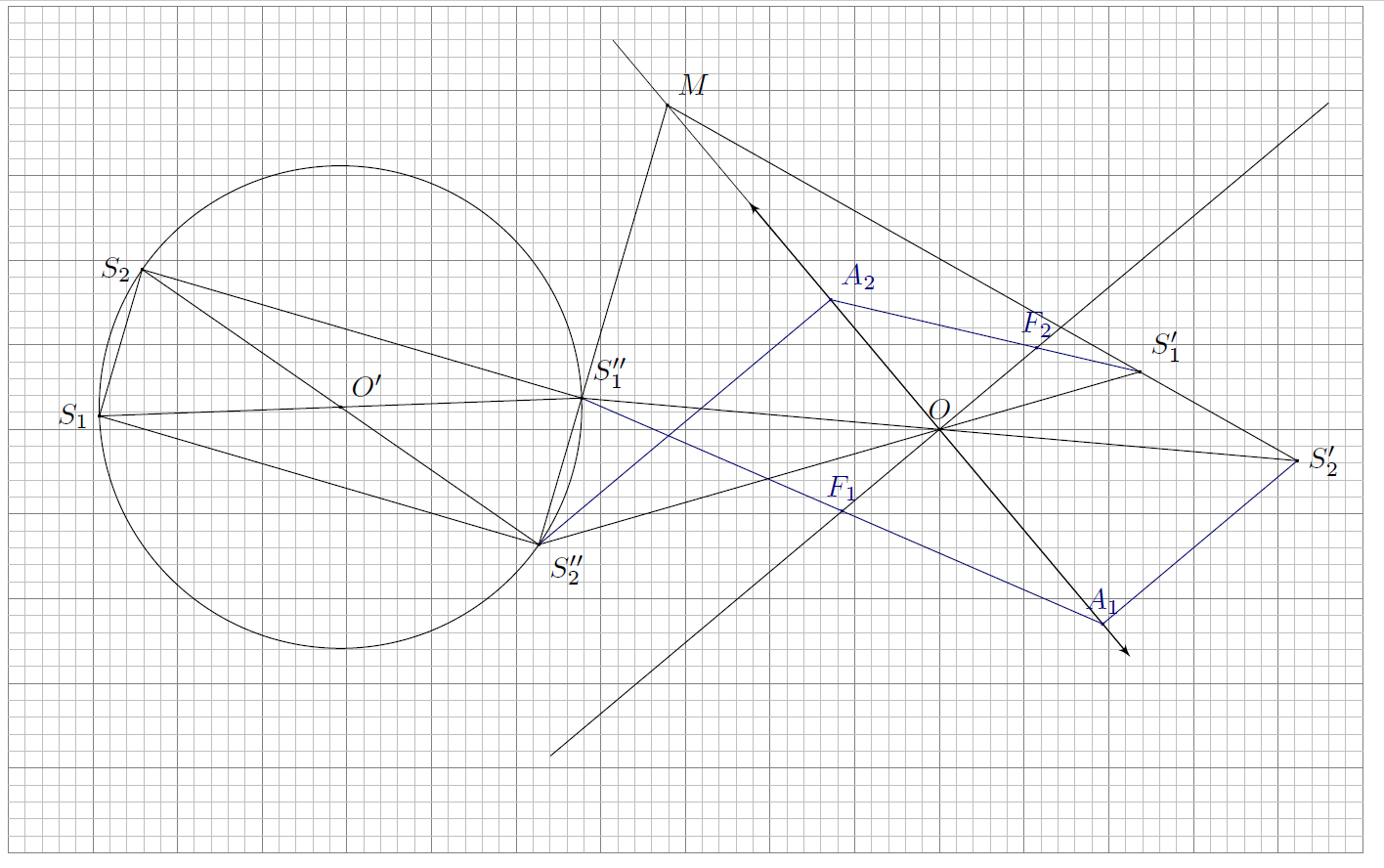
Обозначим изображения источников в "Рыбьем глазе" за $S^{''}_1$ и $S^{''}_2$ в соответствии с индексами. Точки $S^{''}_1$ и $S^{''}_2$ лежат на прямых, проходящих через точку $O$ и точки $S'_1$, $S'_2$.

В данном случае $r_0=a=R$, поэтому изображения точечных источников в "Рыбьем глазе" расположены в его диаметрально противоположных точках, откуда можно сделать вывод, что точки $S_1$, $S_2$, $S^{''}_1$ и $S^{''}_2$ образуют прямоугольник. Отсюда ясно, что точки $S^{''}_1$ и $S^{''}_2$ также лежат и на прямых, проходящих через точки $S_1$ и $S_2$ перпендикулярно отрезку $S_1S_2$. Проводя эти прямые до пересечений, найдём положения точек $S^{''}_1$ и $S^{''}_2$, при этом учитывая, что $S^{''}_1S^{''}_2\parallel{S_1S_2}$.
Величина $S_1S^{''}_1$ является диаметром шара, измеряя который найдём:

B2  ^0.10 Соответствует ли изображение $S'_1$ источнику $S_1$? Ответ обоснуйте.

Как видно из построений в пункте $\textbf{B1}$:

B3  ^1.20 Найдите фокусное расстояние линзы $F$.

Проведём прямые, проходящие через пары точек $\left(S^{'}_1, S^{'}_2\right)$ и $\left(S^{''}_1, S^{''}_2\right)$ до пересечения в точке $M$. Эта точка принадлежит плоскости линзы. Поскольку положение главного оптического центра $O$ нам известно, сразу восстановим плоскость линзы и её главную оптическую ось.

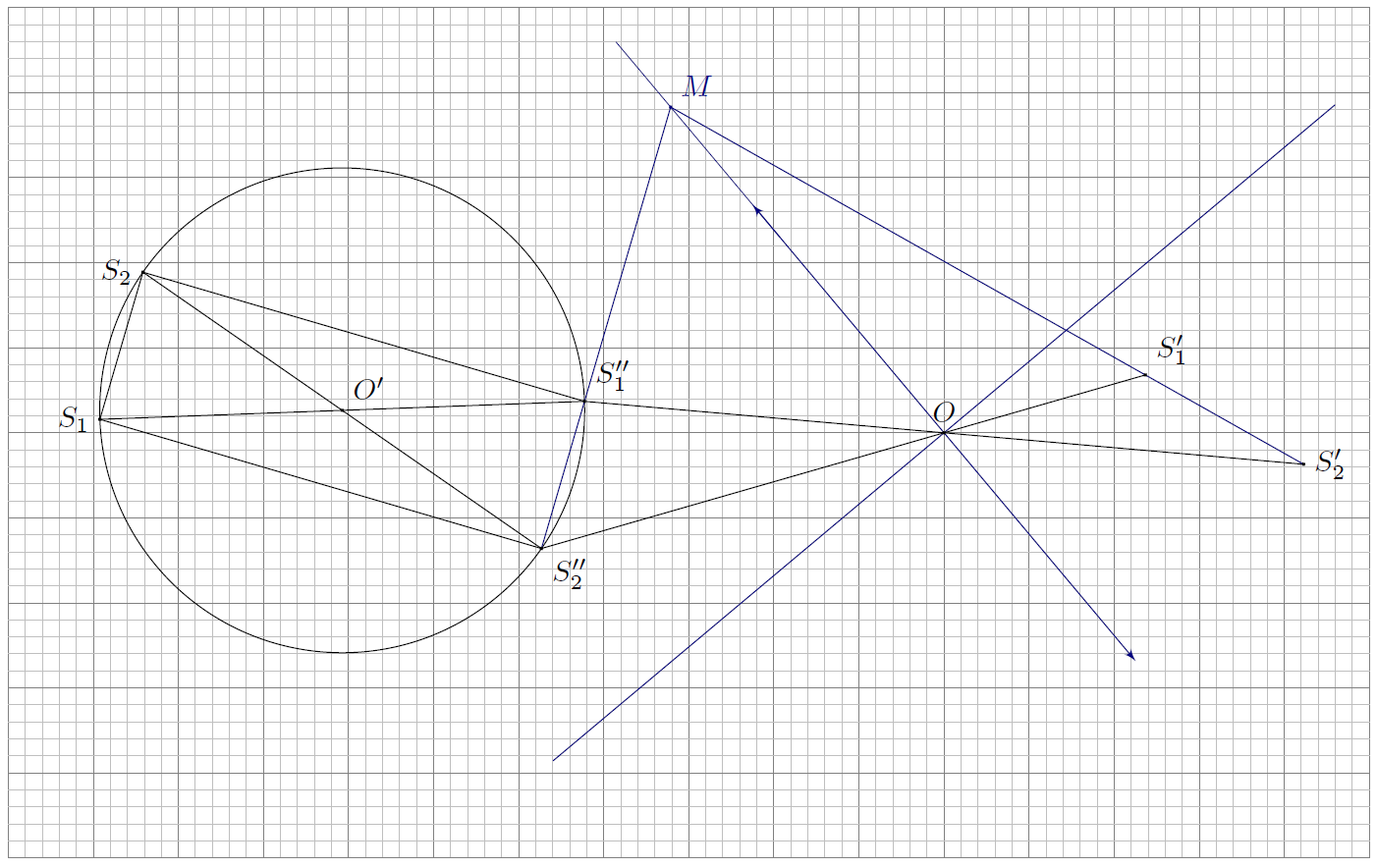
Луч, идущий через изображение $S'_2$ параллельно главной оптической оси, до преломления в точке $A$ проходит через фокус линзы $F$. Проведя данный луч, находим:

C1  ^0.50 Найдите $\Delta{\varphi}$. Ответ выразите через $\alpha$, $n_1$, $a$ и $R$.

Воспользуемся решением пункта $\textbf{A5}$. В точке $B$, находящейся на расстоянии $R+\displaystyle\frac{a^2}{R}$ от точки преломления луча $A$ произошла бы фокусировка лучей, вышедших одновременно из точки $A$.
Обозначим показатель преломления "Рыбьего глаза" на поверхности за $n_0=\displaystyle\frac{n_1}{1+\displaystyle\frac{R^2}{a^2}}$ .
Тогда угол преломления луча $\theta=\displaystyle\frac{\alpha}{n_0}$. За время движения луча от точки $A$ до точки $B$ вектор скорости луча повернулся бы на угол $2\theta$. Поскольку мы работаем в параксиальном приближении:

C2  ^0.30 $\Delta{\alpha}$ можно представить как $\Delta{\alpha}=k\alpha$.
Найдите коэффициент пропорциональности $k$. Ответ выразите через $n_1$, $R$ и $a$.

Найдём угол $\beta$:
$$\pi-\alpha+\beta=2\pi-(\pi-\Delta{\varphi})-2\theta\Rightarrow{\beta=\alpha+\Delta{\varphi}-2\theta}=\alpha\left(1+\displaystyle\frac{2(R^2-a^2)}{n_1a^2}\right)
$$
При этом полный угол поворота луча $\Delta{\alpha}$ равен
$$\Delta{\alpha}=\alpha+\beta=2\alpha\left(1+\displaystyle\frac{(R^2-a^2)}{n_1a^2}\right)
$$
откуда:

C3  ^0.20 Выразите фокусное расстояние $F$ «Рыбьего глаза» через $R$ и $k$.

Тогда для фокусного расстояния имеем:
$$F=R-\displaystyle\frac{\beta R}{\Delta{\alpha}}
$$
или же:

C4  ^1.00 При фиксированных значениях $n_1$ укажите, собирающей или рассеивающей является линза при разных значениях параметра $a$. Ответ обоснуйте.
Постройте графики зависимости фокусного расстояния $F(x)$ от параметра $x=\cfrac{R}{a}$ при всех его возможных значениях для $n_1=1.5;2.0;2.5;3.0;4.0$ и $R=5~\text{у.е}$.

Подставляя значение $k$, получим:
$$F=\displaystyle\frac{R}{2\left(1+\displaystyle\frac{R^2-a^2}{n_1a^2}\right)}
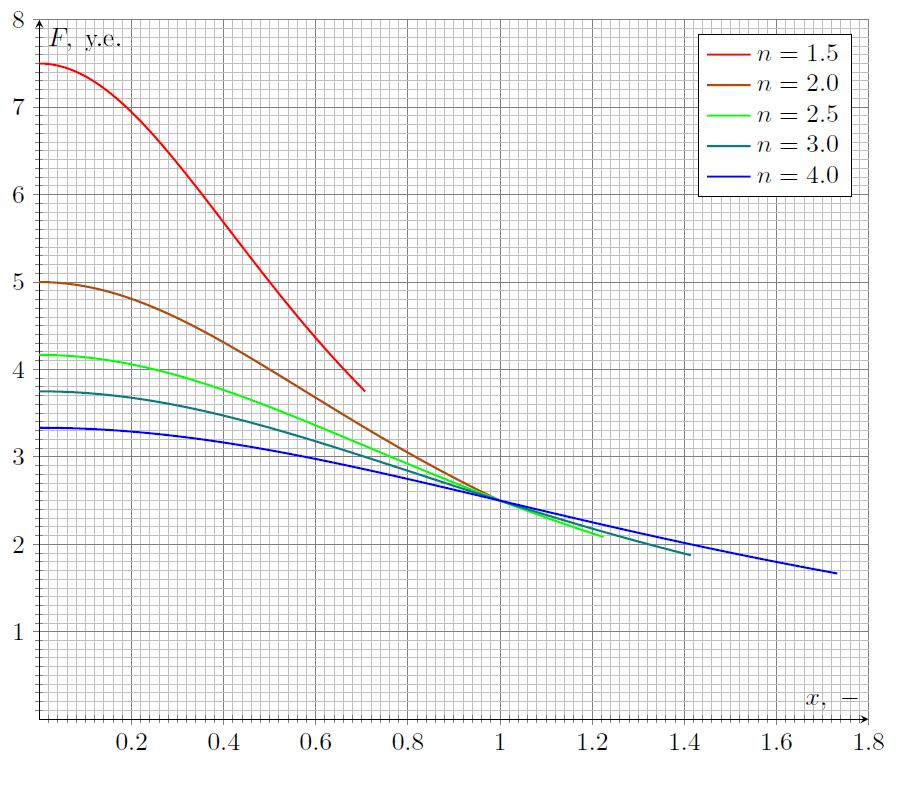
$$
Поскольку $n_1>1$, знаменатель выражения для $F$ всегда положительный.

На графике приведены зависимости $F(x)$ для значения $R=5~\text{у.е}$ при $n_1=1.5;~2.0;~2.5;~3.0;~4.0$ ( сверху-вниз ).
При этом значение параметра $\cfrac{R}{a}\leq{\sqrt{n_1-1}}$

D1  ^0.60 Найдите зависимость координаты $y$ пучка на экране от $h< h_1$ в эксперименте с линзой. Ответ выразите через $h$, $L$, $F_0$, $F$ и $R$.

В параксиальном приближении угол падения $\alpha=\cfrac{h}{R}$. После прохождения рыбьего глаза пучок движется под углом $\Delta\alpha=k\alpha$ к главной оптической оси линзы, причём так, будто бы он испущен из её фокуса.
Тогда он пересекается плоскость линзы в точке с координатой $y_1$, равной:
$$y_1=k\alpha(L-F_0)
$$
Пучок параллельных лучей собирается в фокальной плоскости линзы. Исходя из этого восстановим ход пучка после прохождения линзы. Пусть после прохождения линзы пучок движется под углом $\gamma$ к её главной оптической оси. Тогда:
$$\gamma F+y_1=\Delta\alpha F
$$
откуда:
$$\gamma=\Delta\alpha\left(1-\frac{L-F_0}{F}\right)
$$
Для координаты $y$ пучка на экране получим:
$$y=y_1+\gamma L=(k+1)\alpha\left(L-(L-F_0)\left(\frac{L}{F}-1\right)\right)
$$
или же:

D2  ^0.40 Найдите зависимость координаты $y$ пучка на экране от $h< h_1$ в эксперименте без линзы. Ответ выразите через $h$, $L$, $F_0$, $F$ и $R$.

При значении $h=h_1$ на графике наблюдается скачок, обусловленный тем, что пучок света не пересекает плоскость линзы и сразу падает на экран. Сразу находим:
$$y=k\alpha(2L-F_0)
$$
или же:

D3  ^0.20 Найдите с точностью до третьей значащей цифры значения фокусного расстояния «Рыбьего глаза» $F_0$ и коэффициента пропорциональности $k$.

Для $F_0$ имеем:
$$F_0=\frac{R}{k}
$$
Тогда из выражения для $k_2$ находим:

D4  ^0.30 Определите численное значение радиуса линзы $r$.

В момент скачка луч проходит через край линзы, не преломляясь в ней. Пусть координата $y$ пучка на экране при это равна $H'=12,7~\text{см}$. Из подобия треугольников находим:
$$\frac{r}{L-F_0}=\frac{H'}{2L-F_0}
$$
откуда:
$$r=\frac{(L-F_0)H'}{2L-F_0}
$$
После численной подстановки:

D5  ^0.30 Найдите с точностью до третьей значащей цифры численное значение фокусного расстояния линзы $F$. Собирающая или рассеивающая эта линза?

Из выражения для $k_1$ находим:
$$F=\frac{kL(L-F_0)}{k(2L-F_0)-k_1R}=\frac{L(L-F_0)}{2L-F_0(1+k_1)}
$$
После численной подстановки находим:

D6  ^0.60 Получите точное выражение для $\Delta{\varphi}$. Ответ выразите через $\alpha$, $n_1$, $a$, $R$.

Радиус окружности, по которой движется пучок, равен:
$$R_0=\frac{R^2+a^2}{2R\sin\theta}
$$
Из теоремы косинусов найдём расстояние между центрами окружности и "рыбьего глаза":
$$L^2=R^2+R^2_0-2RR_0\sin\theta=R^2+\cfrac{(R^2+a^2)^2}{4R^2\sin^2\theta}-(R^2+a^2)
$$
Подставляя $\sin\theta$, получим:
$$L^2=a^2\left(\frac{n^2_1a^2}{4R^2\sin^2\alpha}-1\right)
$$
Воспользуемся теоремой синусов:
$$\frac{L}{\cos\theta}=\frac{R}{\sin\cfrac{\Delta{\varphi}}{2}}
$$
Таким образом:
$$\Delta{\varphi}=2\arcsin\frac{R\cos\theta}{L}
$$
откуда находим:

D7  ^0.60 Получите уравнение, определяющее $n_1$. Уравнение должно содержать только $n_1$, $\alpha_0$ и $k$.

Для угла поворота пучка имеем:
$$\Delta{\alpha}=2\alpha-2\theta+\Delta\varphi
$$
Отсюда:
$$\Delta\alpha=2\alpha-2\arcsin\left(\frac{\sin\alpha(R^2+a^2)}{n_1a^2}\right)+2\arcsin\left(\frac{R}{a}\sqrt{\frac{1-\cfrac{\sin^2\alpha(R^2+a^2)^2}{n^2_1a^4}}{\cfrac{n^2_1a^2}{4R^2\sin^2\alpha}-1}}\right)
$$
Из выражения для коэффициента $k$ находим:
$$\frac{R^2}{a^2}=1+\frac{n_1(k-2)}{2}
$$
Подставляя, получим:
$$\Delta\alpha=2\alpha-2\arcsin\left(\frac{\sin\alpha}{n_1}\left(2+\frac{n_1(k-2)}{2}\right)\right)+2\arcsin\left(\sqrt{\left(1+\frac{n_1(k-2)}{2}\right)\left(\cfrac{1-\left(\cfrac{\sin\alpha}{n_1}\left(2+\cfrac{n_1(k-2)}{2}\right)\right)^2}{\cfrac{n^2_1}{4\sin^2\alpha\left(1+\cfrac{n_1(k-2)}{2}\right)}-1}\right)}\right)
$$
Асимптотическое стремление к бесконечности достигается при $\Delta\alpha=\cfrac{\pi}{2}$. Тогда уравнение на $n_1$ следующее:

D8  ^1.00 Внесите в таблицу в листе ответов значения углов $\theta(n_1)$ и $\Delta{\varphi}(n_1)$ с точностью до сотых градуса для указанных значений $n_1$.
Найдите с точностью до второй значащей цифры значения $n_1$ и $a$.

Решая уравнение на $n_1$, находим:

Найдём и $a$:
$$a=\frac{R}{\sqrt{1+\cfrac{n_1(k-2)}{2}}}
$$