
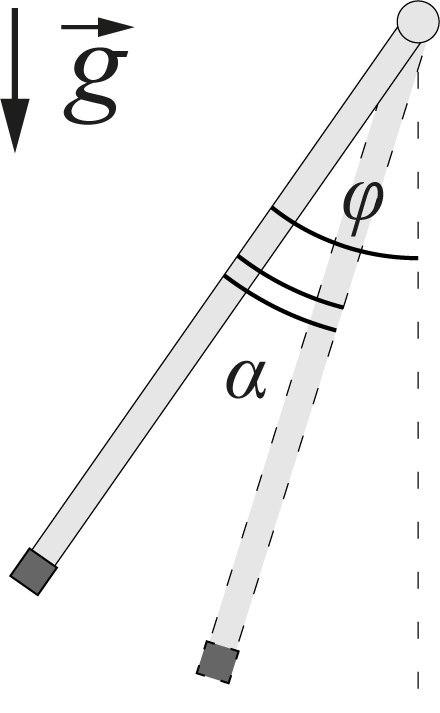
Из выражения следует, что при $0\leq{\alpha}\leq{2\varphi}$ частица разгоняется, при $2\varphi<\alpha\leq{\pi}$ — замедляется, и при $\pi<\alpha\leq{2(\pi+\varphi)}$ вновь разгоняется. Запишем закон сохранения механической энергии в произвольный момент времени
$$-mgL\cos\varphi+FL\alpha=-mgL\cos(\varphi-\alpha)+\frac{mv^2}{2}
$$
Если остановка частицы происходит при значениях $\alpha<\pi$, то в дальнейшем частица будет двигаться в области, ограниченной двумя положениями её нулевой скорости. Если же частица преодолевает данный барьер, то при $\alpha>\pi$ её кинетическая энергия будет возрастать. Таким образом, необходимым условием полного оборота является ненулевая скорость в момент $\alpha=\pi$, или же
$$v^2={\frac{2{\pi}LF}{m}-4gL\cos\varphi}\geq{0}
$$
Выразим $cos(\varphi)$ из первого соотношения
$$\cos\varphi=\sqrt{1-\left(\frac{F}{mg}\right)^2}
$$
Из последних двух соотношений получим
$$\frac{{\pi}F}{2}\geq{\sqrt{(mg)^2-F^2}}
$$
Также из условия равновесия стержня ясно, что
$$F\leq{mg}
$$
и окончательный диапазон значений $F$