Pho.rs: Тише, мыши...

Решение

W21

A1 ^5.00 Найдите максимально возможное начальное расстояние $L_{max}$ между мышами и Леопольдом.

Предисловие: Последняя “перестрелка” Леопольда и мышей произошла в 2002 году, с тех пор мыши кота не беспокоили. Спустя 18 лет, в 2020 году, нашлись новые подводные камушки для легендарной рогатки и мыши решили “тряхнуть стариной”.
Примечание: в ходе перестрелки никто из животных не пострадал.

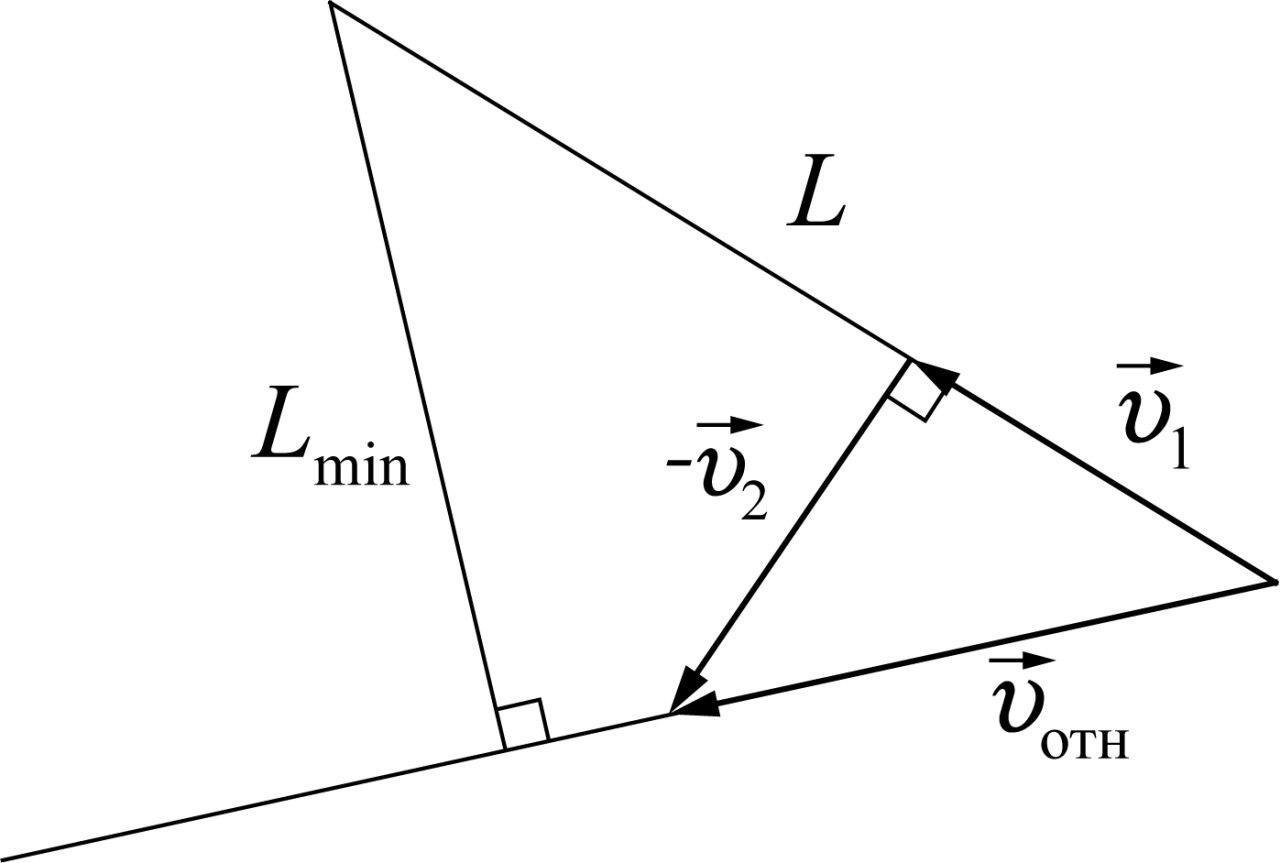
В системе отсчёта Леопольда камень движется прямолинейно с постоянной скоростью $v_{отн}$. Расстояние от Леопольда до камня минимально, когда соединяющий их отрезок перпендикулярен вектору относительной скорости (см. рис.). Из подобия треугольников определим перемещение камня относительно Леопольда:

$$S_{отн}=L \frac{v_1}{v_{отн}} =v_{отн}t$$
откуда
$$L=\frac{v^2_{отн}t}{v_1}$$

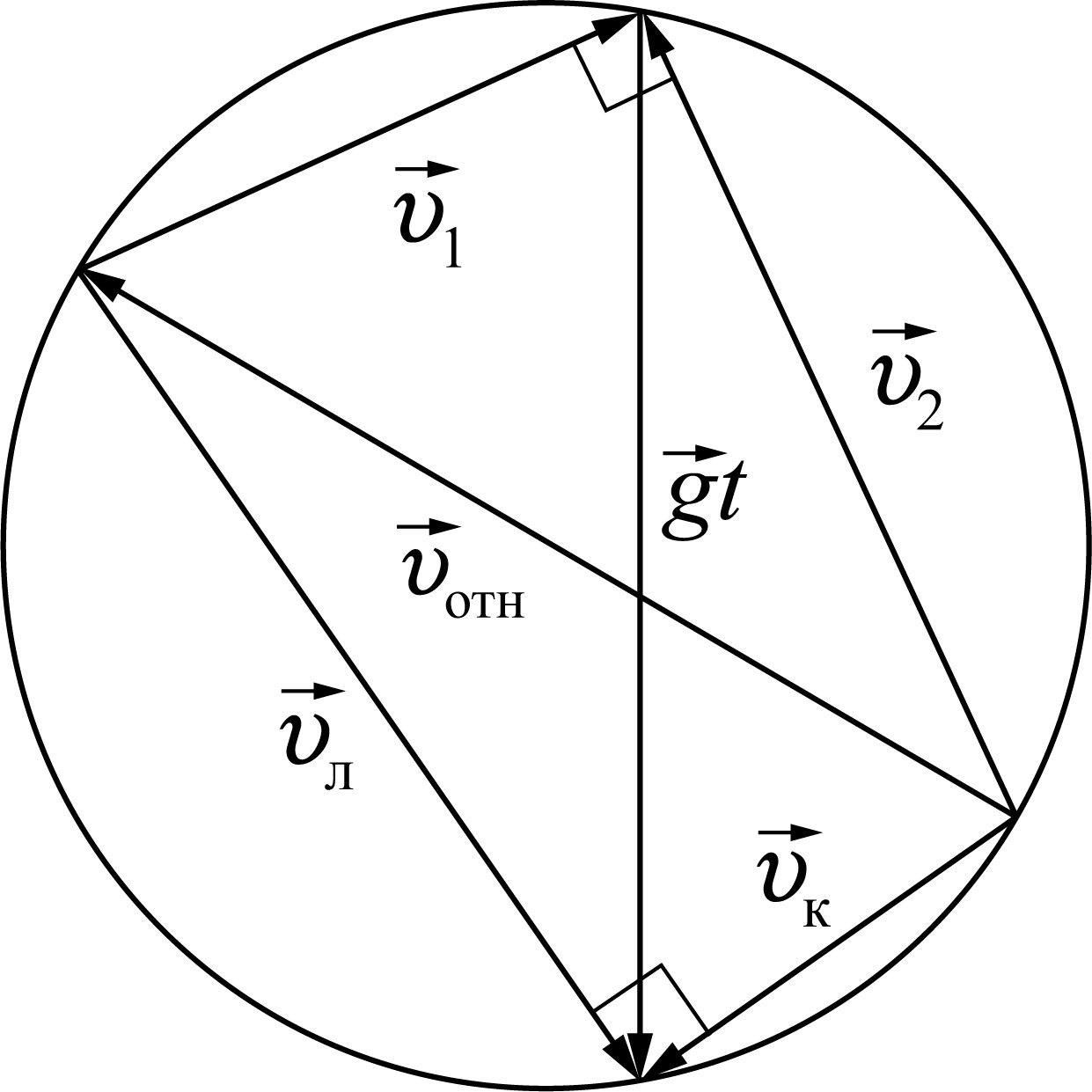
Найдем максимально возможное время, через которое скорости камня и Леопольда вновь станут перпендикулярны. Построим треугольники скоростей камня и Леопольда для максимального сближения, объединив их в один четырёхугольник. Заметим, что этот четырёхугольник можно вписать в окружность, поскольку сумма противоположных углов равна 180°. Диаметр окружности фиксирован и равен $v_{отн}$. Поскольку $L$ максимально при максимальном значении $t$, необходимо, чтобы вторая диагональ четырёхугольника, равная $gt$, также была максимальна. Это достигается если $gt$ – диаметр данной окружности. Таким образом,

$$t_{max}=\frac{v_{отн}}{g}$$
и окончательно:
$$L_{max}=\frac{v^3_{отн}}{gv_1}=\frac{\left({v^2_1}+{v^2_2}\right)^\frac{3}{2}}{gv_1}$$

Второе решение

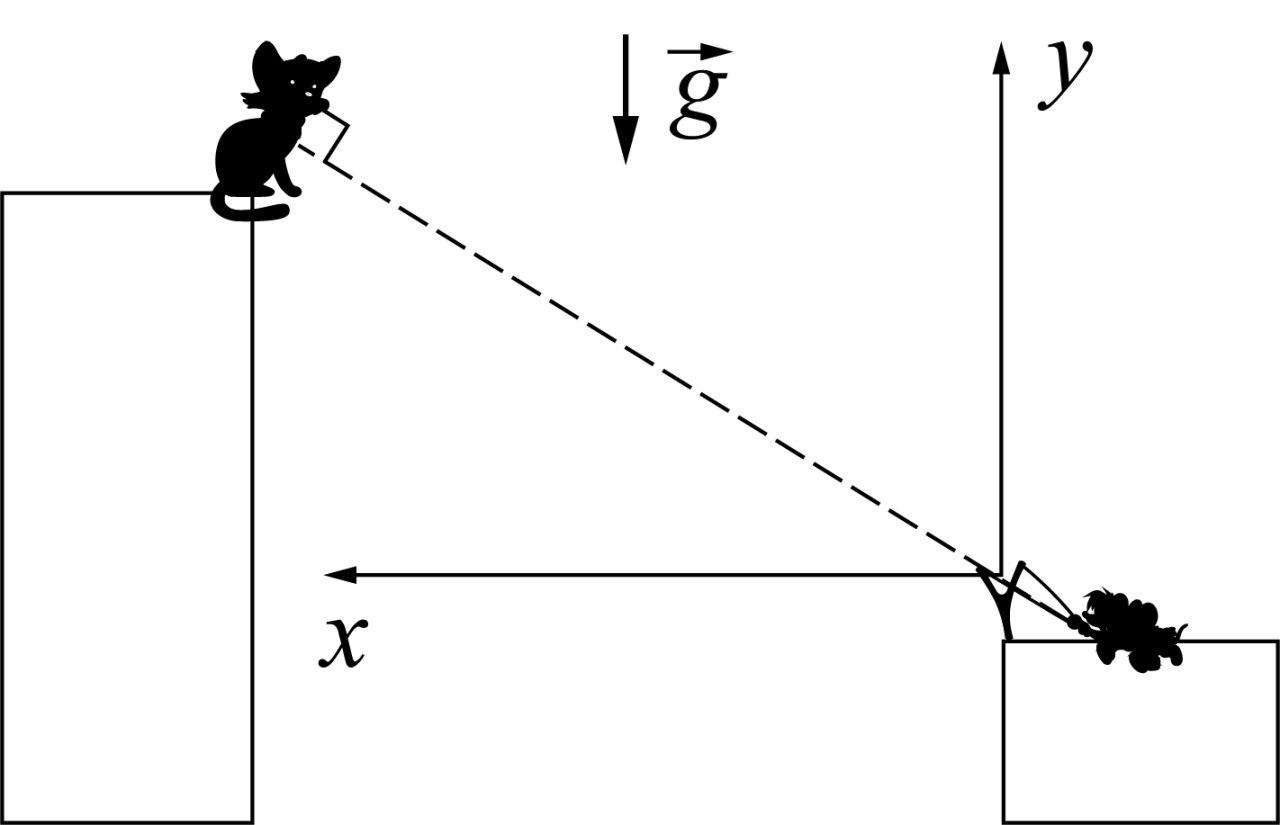
Введём систему координат, как показано на рисунке. Пусть угол, под которым брошен камень к горизонту, равен $\alpha$. Получим зависимости координат, проекций скоростей и расстояния между камнем и Леопольдом от времени.

$$x_к=v_1t\cos\alpha;~y_к=v_1t \sin⁡\alpha-\frac{gt^2}{2}
$$
$$v_{yк}=v_1\sin⁡\alpha -gt;~v_{xк}=v_1\cos\alpha
$$
$$x_л=L\cos⁡\alpha-v_2t\sin⁡\alpha;~y_л=L\sin⁡\alpha+v_2t\cos⁡\alpha-\frac{gt^2}{2}
$$
$$v_{yл}=v_1\cos\alpha-gt;~v_{xл}=-v_1\sin⁡\alpha
$$
Расстояние между Леопольдом и камнем назовём $l$.
$$l^2=(x_к-x_л )^2+(y_к-y_л )^2
$$
$$l^2=(L \cos⁡\alpha -(v_1\cos⁡\alpha +v_2\sin\alpha )t)^2+(L \sin⁡α-(v_1\sin⁡\alpha -v_2\cos⁡\alpha )t)^2
$$
$$l^2=L^2-2v_1Lt+(v^2_1+v^2_2 ) t^2
$$
Минимальное значение $l$ достигается в вершине параболы в момент времени
$$\tau=Lv_1/(v^2_1+v^2_2 )$$
Для нахождения максимально возможного значения $L$ необходимо найти максимально возможное значение $\tau$.
Пусть в момент времени $\tau$ скорость камня направлена под углом $\beta$ к горизонту. Поскольку в данный момент времени скорости Леопольда и камня перпендикулярны, скорость Леопольда направлена под углом $90-\beta$ к горизонту. Значит, для этого момента времени можно записать
$$v_{yк}/v_{xк} =-v_{xл}/v_{yл}$$
$$(v_1\sin⁡\alpha -g\tau )(v_2\cos\alpha-g\tau)-v_1v_2\sin⁡\alpha \cos⁡\alpha =0$$
Из последнего соотношения находим $\tau$
$$\tau=\frac{(v_1\sin⁡\alpha +v_2\cos(⁡\alpha))}{g}$$
Комбинируя два способа получения $\tau$, получим зависимость расстояния от угла броска камня
$$L=\frac{(v^2_1+v^2_2 )(v_1\sin⁡\alpha+v_2\cos\alpha)}{gv_1}
$$
Для нахождения максимума L необходимо найти максимум величины $v'=(v_1\sin⁡\alpha +v_2\cos⁡\alpha )$
$$(v'-v_1\sin\alpha)^2=v^2_2(1-\sin^2\alpha )
$$
$$(v^2_1+v^2_2)\sin⁡^2\alpha -2v' v_1\sin⁡\alpha+{v^2}'-v^2_2=0
$$
Найдём дискриминант квадратного уравнения относительно \sin⁡α
$$D=4{v^2}' v^2_1-4(v^2_1+v^2_2 )({v^2}'-v^2_2 )
$$
$$D=4v^2_2 (v^2_1+v^2_2 )-{v^2}')
$$
Максимальное значение $v'$ достигается при нулевом дискриминанте и равно
$$v'=\sqrt{v^2_1+v^2_2 }
$$
Таким образом, максимально возможное значение

Ответ: $$L_{max}=\frac{(v^2_1+v^2_2 )^\frac{3}{2}}{gv_1}$$

A2 ^5.00 Найдите значения скоростей $v_1$ и $v_2$. Ускорение свободного падения $g=9,8~\text{м}/{\text{с}^2}$.

Заметим, что вектор средней скорости камня в момент фотографии равен $\frac{\vec{v_{отн}}}{2}$, в вектор средней скорости Леопольда $-\frac{\vec{v_{отн}}}{2}$. Это значит, что перемещения камня и Леопольда равны по модулю и противоположны по направлению. Пусть $D$ - середина отрезка $AC$. Тогда из условия равенства перемещений по модулю следует, что $BD=\frac{L}{2}$, а также, что треугольник $DCB$ - прямоугольный, причём $\frac{v_2}{v_1}=\frac{CD}{BC}$. Измеряя $BC$, $BD$ и $CD$, получим

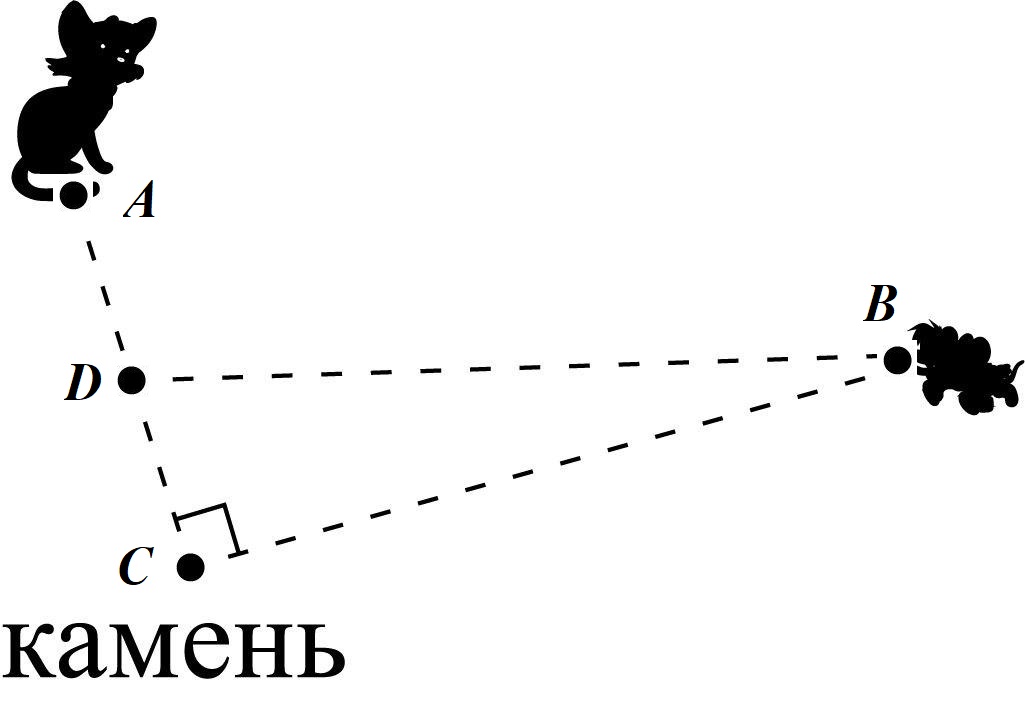
$$v_2=\frac{CD}{BC}v_1$$ $$BD=\sqrt{BC^2+CD^2}=\frac{(v_1^2+v_2^2)^\frac{3}{2}}{2gv_1}=\frac{(BC^2+CD^2)^\frac{3}{2}}{BC^3}\frac{v_1^2}{2g}$$

Ответ:

$$v_1=\sqrt{\frac{2gBC}{BC^2+CD^2}}BC=10,\!8~\text{м/с}$$
$$v_2=\sqrt{\frac{2gBC}{BC^2+CD^2}}CD=2,\!7~\text{м/с}$$

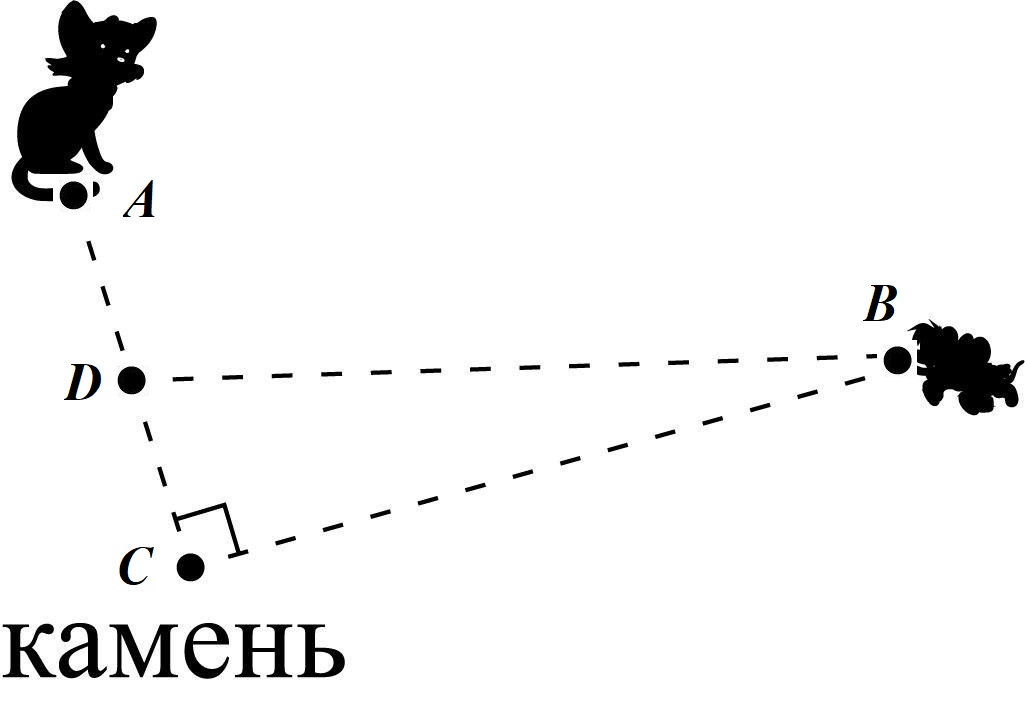
Второе решение

Выражение для $\sin\alpha$ из решения предыдущего пункта
$$\sin\alpha=\frac{v_1}{\sqrt{v^2_1+v^2_2}}
$$
Найдём координаты камня и расстояние между ним и Леопольдом в момент времени $\tau$
$$x_к=v_1\tau\cos\alpha=\frac{v_1v_2}{g}
$$
$$y_к=v_1\tau\sin\alpha-\frac{g{\tau}^2}{2}=\frac{v^2_1}{g}-\frac{v^2_1+v^2_2}{2g}=\frac{v^2_1-v^2_2}{2g}
$$
$$l=\frac{(v^2_1+v^2_2 )v_2}{gv_1}
$$
Таким образом, перемещение камня
$$S_к=\frac{v^2_1+v^2_2}{2g}
$$
Измеряя перемещение камня, а также расстояние между ним и Леопольдом, мы получим систему из двух уравнений с двумя неизвестными.
Выразим начальные скорости через $l$ и $S_k$
$$\frac{S_k}{l}=\frac{v_1}{2v_2}
$$
$$v_2=\frac{l}{2S_k}v_1
$$
$$S_k=\frac{1+\frac{l^2}{4S_k^2}}{2g}v_1^2
$$
$$v_1=\sqrt{\frac{8gS_k}{l^2+4S_k^2}}S_k=10,\!8~\text{м/с}
$$
$$v_2=\sqrt{\frac{2gS_k}{l^2+4S_k^2}}l=2,\!7~\text{м/с}
$$