A1  ^11.00 Определите экспериментально коэффициент трения качения $k$ цилиндра, катающегося по деревянному бруску. Опишите способ измерения и зарисуйте схему установки.

Уравновесим линейку на ребре бруска, тем самым определим положение центра масс линейки: $x_r=248~мм$. Используя линейку как рычаг, определим отношение масс $M/m$ цилиндра и линейки

$$M/m=3.44±0.22.$$

Закрепим линейку в качестве стержня на основание цилиндра используя клейкую массу. Сторону линейки со шкалой направим в сторону цилиндра: так удобнее определять положение линейки относительно цилиндра. На край стола закрепим лист с начерченными линиями под разными углами к вертикали. Запустим колебания системы цилиндра и стержня. Величину амплитуды фиксируем по совпадению с линиями на листе. Линии на листе не обязательно рисовать как лучи из одного центра: можно подобрать положения так, чтобы линия совпадала с наклонённой линейкой при соответствующем положении цилиндра.

Энергия системы при колебаниях, выраженная через угловую амплитуду $\varphi$:

$$W=mgd(1-cos⁡\varphi )≈mgd \varphi^2/2.$$

При повороте цилиндра со стержнем на угол $d\alpha$ момент силы реакции опоры совершает работу:

$$\delta A=-M⋅d\alpha=-k(m+M)g⋅d\alpha.$$

Остальные силы работы не совершают. Заметим, что даже когда система находится в положении равновесия, но движение ещё не закончилось, система всё равно характеризуется угловой амплитудой $\varphi$. Изменение энергии системы при повороте на малый угол $d\alpha$:

$$dW=mgd⋅\varphi d\varphi=-k(m+M)g⋅d\alpha.$$

Убыль энергии за 1/4 периода (здесь знак «$\Delta$» означает убыль, а не изменение):

$$mgd⋅\varphi⋅\Delta\varphi_{T/4} = k(m+M)g⋅\varphi.$$

За $N$ периодов величина убыли амплитуды будет в $4N$ раз больше. Выразим коэффициент трения качения

$$k=\frac{m}{m+M} \frac{d⋅\Delta\varphi_N}{4N}.$$

$x_{up}$, мм; $d$, мм; $\varphi_0$, °; $\varphi$, °; $N$ ; $k$, мм; $\Delta k$, мм 0;186,5;30;10;18;0,23;0,019 20;166,5;30;10;16;0,231;0,02 40;146,5;30;10;14;0,233;0,022 40;146,5;40;10;21;0,233;0,016 40;146,5;40;20;13;0,25;0,025

В итоге, получается коэффициент трения качения
$$k=(0,24 \pm 0,02)~мм.$$

A2  ^4.00 Определите экспериментально коэффициент трения скольжения $\mu$ картона цилиндра о дерево. Приведите способ измерения и схему установки.

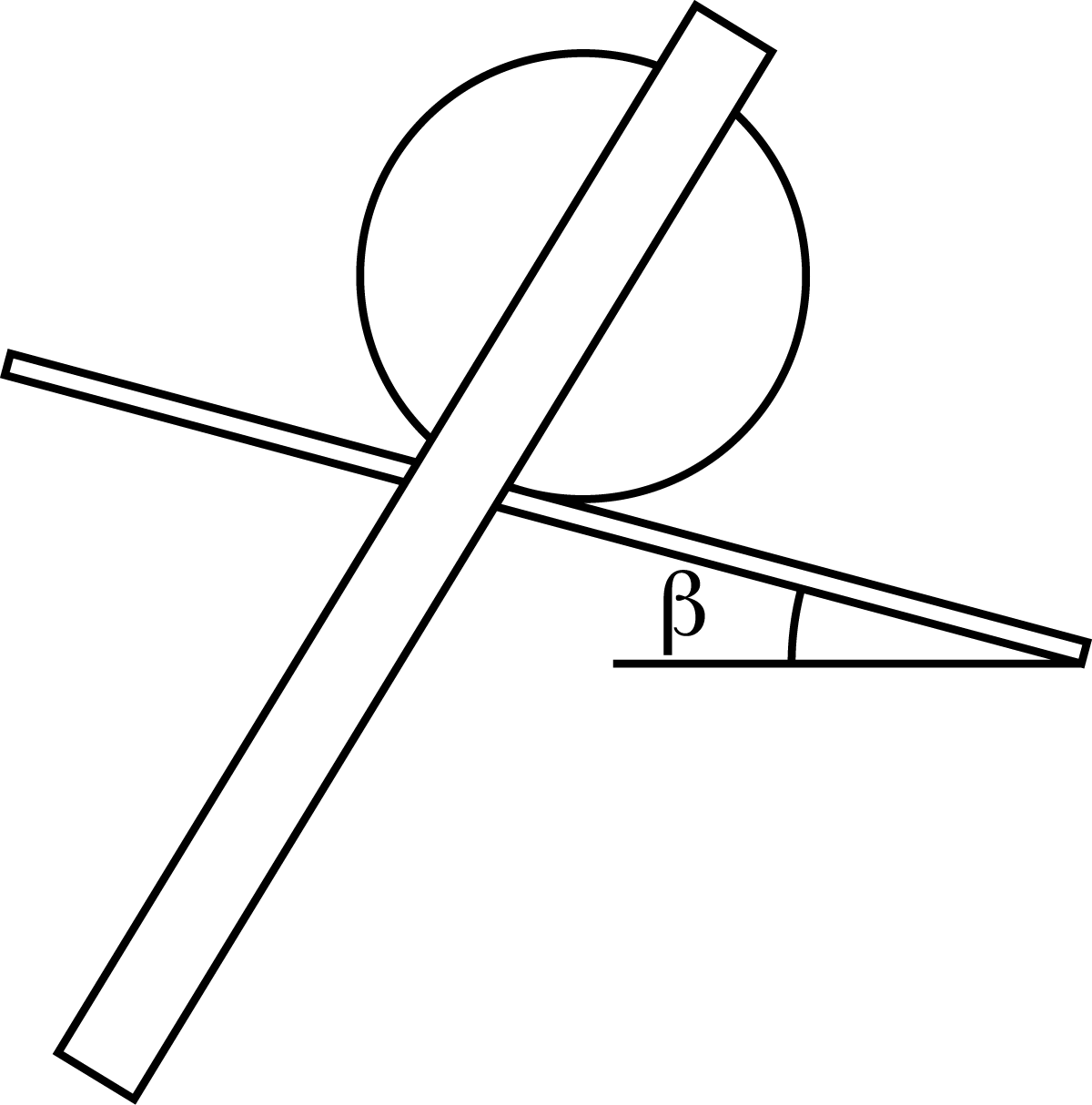
Используя клейкую массу закрепим линейку в качестве стержня на основание цилиндра. Поместим данную систему на брусок. Начнем наклонять брусок (рис. 1). При некотором угле наклона $\beta$ бруска к горизонту система начнёт скользить.
Коэффициент трения
$$ \mu = \mathrm{tg}~ ⁡\beta=\mathrm{tg}~⁡ (17° \pm 1°)= 0,31 \pm 0,02 .$$