В тонких пленках $\rm In-O$ при низких температурах (порядка $1~\text{K}$) наблюдается управляемый внешним магнитным полем фазовый переход сверхпроводник-диэлектрик (переход происходит при изменении внешнего магнитного поля $B$).

Часть А. Критические параметры (6.8 балла)

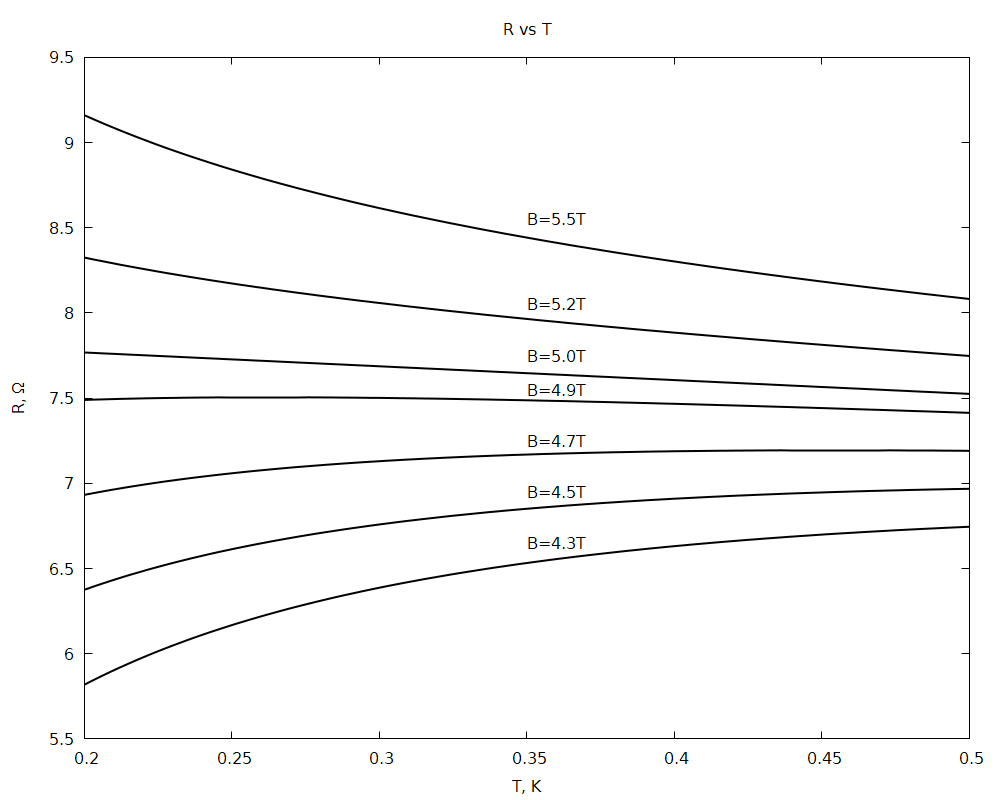
В таблице «Экспериментальные данные» представлены измерения зависимостей $R(T)$, где $R$ – сопротивление образца, $T$ – температура, при разных внешних магнитных полях $B$. Погрешность измерения сопротивления $\varepsilon(R)=0.5\%$. На графике (см. рис) приведены примерные виды зависимостей $R(T)$ для некоторых значений $B$, указанных в таблице. Предположим, что зависимость сопротивления $R(T,B)$ имеет следующий вид: $$R(T,B) = R_C - \gamma T + A \left( B - B_C \right) T^{\alpha}, $$ где $A, R_C, B_C$ — некоторые параметры, связанные со свойствами образца. Если на кривой $R(T)$ есть точка перегиба (то есть $\dfrac{\partial R}{\partial T}=0$), то обозначим ее координаты, как $\left(T_\text{п}, R_\text{п}\right)$. Примечание: Для функции двух переменных аналогом производной выступает частная производная согласно определениям: \[ \frac{d}{dx}f(x) = \lim_{\Delta x \to 0} \frac{ f(x+\Delta x) - f(x)}{\Delta x} \] \[ \frac{\partial}{\partial x}f(x,y) = \lim_{\Delta x \to 0} \frac{ f(x+\Delta x, y) - f(x,y)}{\Delta x} \quad \] Фактически, при вычислении частой производной по $x$ мы полагаем $y$ константой и наоборот, например: \[ f(x,y) = 3x^2 + 2xy,\quad \frac{\partial}{\partial x}f(x,y) = 6x + 2y,\quad \frac{\partial}{\partial y}f(x,y) = 2x \]

A1  ^1.00 Выведите аналитическую зависимость $R_\text{п}$ ($T_\text{п}$).

A2  ^0.40 Определите $B_C$.

A3  ^2.60 Определите $R_C$ двумя способами.

A4  ^2.80 Определите параметры $\gamma$ и $\alpha$.

Часть B.Вероятность описания эксперимента (3.2 балла)

Оценка погрешности физической величины $X$ позволяет рассчитывать вероятность, с которой ее значение лежит в интервале $[a,b]$. Для оценки вероятности $p$ того, что результат эксперимента описывается математическим выражением используется критерий $\chi^2$ (хи-квадрат), рассчитываемый по следующей формуле: \[ \chi^2 = \sum\limits_{i=1}^{N} \left( \frac{R_\text{теор} - R_\text{эксп}}{\Delta R} \right)^2 \] При количестве точек $N=150$ таблица соответствия $p$ и $\chi^2$:

(Таблица вероятностей)

B1  ^2.20 Посчитайте $\chi^2$ (определение в примечании) зависимостей $R(T)$ для каждого $B$.

B2  ^1.00 Используя таблицу из примечания, оцените вероятность согласно которой формула $f={R(T,B)}$ описывает зависимость $R(T,B)$ для любых (укажите каких) $150$ точек.