Бильярд — собирательное название нескольких настольных игр с различными правилами, в которых игрок использует деревянный стержень — кий для передвижения шаров по поверхности стола. Опытный игрок в бильярд знает, насколько важны для правильной игры физические характеристики шаров и кия и как во время игры можно использовать законы физики в свою пользу. В этой задаче мы исследуем некоторые сюжеты, связанные с физикой бильярдных шаров.

Во всех пунктах мы считаем бильярдный шар однородным телом радиуса $R$ с моментом инерции $I=\frac{2}{5} mR^2$ относительно любой оси, проходящей через центр.

Часть A. Sweet spot (1.5 балла)

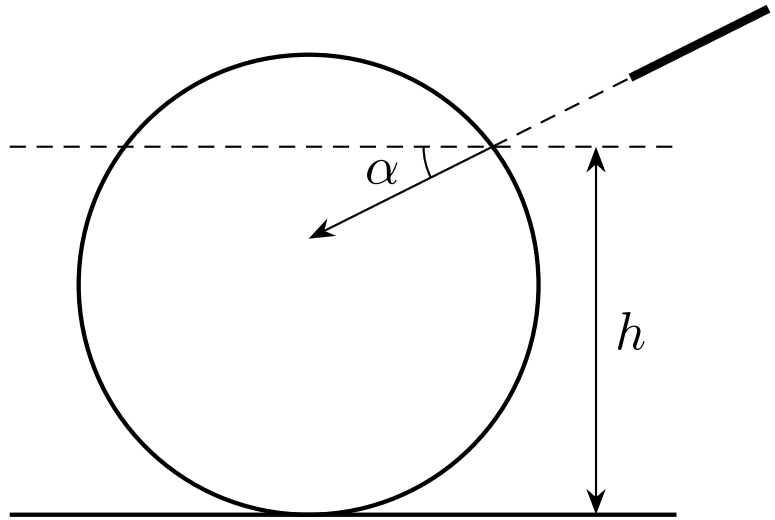
После удара кием о шар в общем случае шар может потерять часть своей начальной скорости, пока устанавливается движение, за счет трения при проскальзывании. Однако, хорошим игрокам в бильярд известна точка (« sweet spot »), при ударе в которую шар не будет терять скорости при движении.

Будем считать, что удар по шару сосредоточен в некоторой точке на высоте $h$ от стола; кий при этом ориентирован под углом $\alpha$ к поверхности стола ($-\pi/2\le\alpha\le\pi/2$, см. рис.). Считайте, что сила удара такова, что при любых $\alpha$ шар не отрывается от стола. Трением о поверхность в этом пункте можно пренебречь.

A1  ^1.00 Определите, при каком соотношении между $h$ и $\alpha$ после удара шар будет двигаться без проскальзывания.

A2  ^0.50 Нарисуйте (качественно) график зависимости $\alpha(h/R)$ с указанием точек, соответствующих $\alpha=0$ и $h=R$.

Часть B. Столкновение бильярдных шаров на столе (4.5 балла)

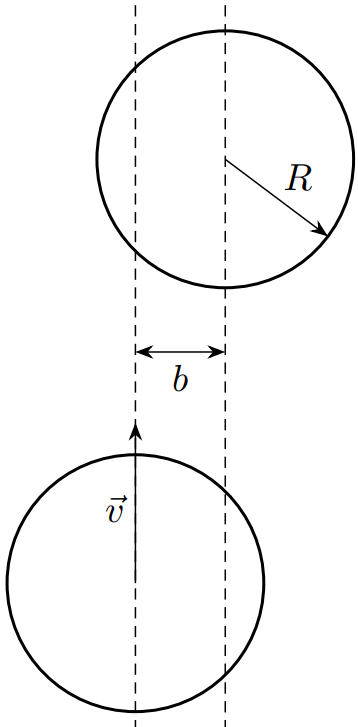
В этой части задачи рассматривается столкновение двух бильярдных шаров. Трением между шарами при столкновении можно пренебречь, а удар — абсолютно упругий. Для начала также пренебрежем и трением о стол.

Пусть бильярдный шар (« биток ») налетает на такой же покоящийся со скоростью $\vec{v}$; относительный прицельный параметр (величина, отмеченная на рис.) равен $\frac{b}{R}<2$.

B1  ^1.00 Найдите скорости шаров после разлёта (модули и направления).

B2  ^0.50 Какой угол образуют скорости шаров после разлёта в такой модели?

Простое предсказание, полученное в предыдущем пункте и часто используемое игроками в бильярд как эмпирическое правило, значительно меняется при учёте трения о поверхность стола. Особенно заметно влияние его на движение « битка ».

B3  ^1.50 Рассмотрим вспомогательную задачу: шар на горизонтальном столе в начальный момент имеет поступательную скорость $\vec{v}=\begin{pmatrix} v_x \\ v_y \end{pmatrix}$ и угловую скорость $\vec\omega=\begin{pmatrix} \omega_x \\ \omega_y \end{pmatrix}$ (вектора $\vec v$ и $\vec\omega$ лежат в плоскости стола). Имеется трение о поверхность, которое прекращается, как только исчезает проскальзывание. Какова будет установившаяся скорость шара (модуль и направление)?

B4  ^0.50 Вернемся к столкновению двух шаров; пусть до удара « биток » двигался без проскальзывания. Под какими углами к начальной скорости теперь направлены установившиеся скорости шаров?

B5  ^0.50 Определите угол $\varphi$ между установившимися скоростями шаров как функцию прицельного параметра $\frac{b}{R}$.

B6  ^0.50 Нарисуйте качественный график зависимости $\varphi(\frac{b}{R})$.

Часть C. Анализ экспериментальных данных (2 балла)

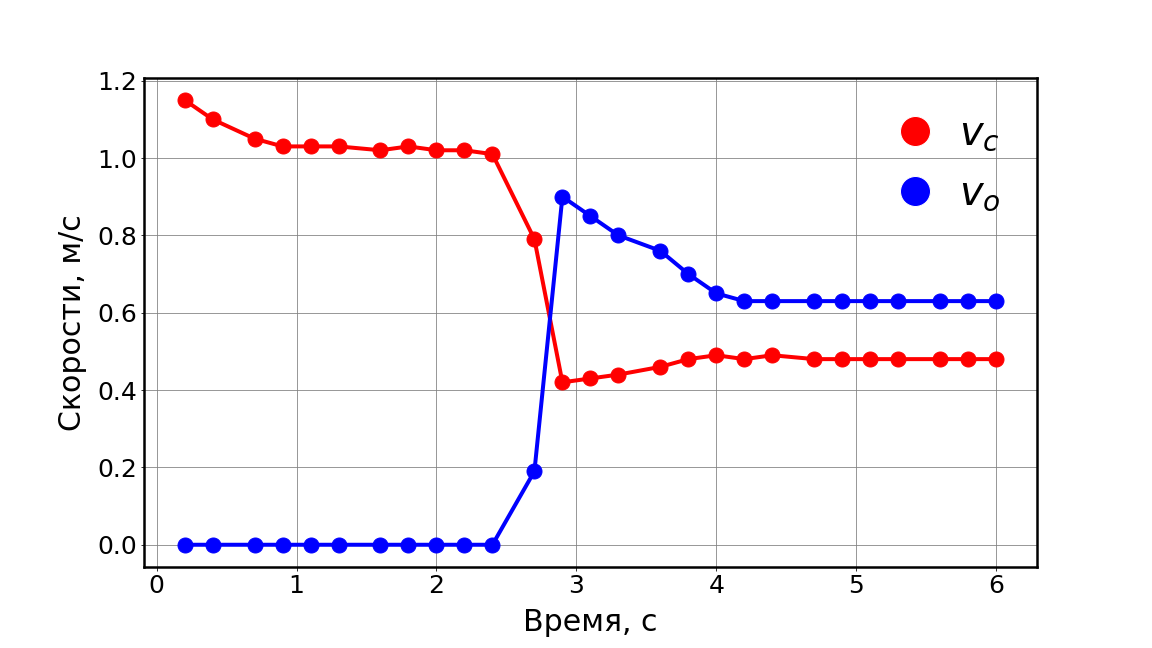
Обратимся к экспериментальным данным, чтобы проверить рассмотренные нами модели. С помощью высокоскоростной съемки была получена зависимость скорости двух сталкивающихся шаров от времени; на графике обозначено $V_c$ — скорость « битка » (cue ball), $V_o$ — скорость изначально неподвижного шара (object ball).

C1  ^0.50 Определите коэффициент трения скольжения. Оцените погрешность полученного значения.

C2  ^0.50 Оцените относительные потери энергии при столкновении шаров.

C3  ^1.00 Определите относительный прицельный параметр $\frac{b}{R}$ для столкновения, используя данные для обоих шаров. Оцените погрешность полученного значения.

Часть D. Модуль Юнга материала бильярдного шара (2 балла)

Известно, что сила $F$, действующая между двумя телами сферической формы, прижатыми друг к другу, зависит от деформации (расстояния, на которое сближаются центры шаров) $h$ как (формула Герца)
$$F=k\,E\,R^{\frac{1}{2}}h^{\frac{3}{2}},$$
где $k$ — численный коэффициент, $k\approx 1$, $E$ — модуль Юнга материала, из которого сделаны шары, $R$ — радиус шара.

D1  ^1.50 Рассмотрим центральный удар ($b=0$) двух одинаковых шаров массы $M$. Первый шар налетает на второй со скоростью $V$. Считая скорость налетающего шара много меньшей скорости звука в материале шара, найдите время столкновения $\tau$ и максимальную деформацию $h_m$.

Указание: считайте известным значение интеграла
$$\int\limits_0^1\frac{dx}{\sqrt{1-x^{5/2}}}\approx 1.5.$$

D2  ^0.50 Оцените модуль Юнга материала шара, исходя из экспериментальных значений: $\tau=310~мкс, V=7.0~м/с, M=280~г, R=6.8~см$.