Pho.rs: Оптический волновод

Условие

Edu

ZH21

В настоящее время для передачи энергии и информации широко используются различные волноводы. Распространение электромагнитных волн в волноводах существенно отличается от рас-пространения волн в свободном пространстве и в данной задаче вам необходимо описать распространение электромагнитных волн в простейшем плоском волноводе.

Описание волн

Плоская монохроматическая электромагнитная волна, распространяющаяся вдоль оси $Ox$, описывается функцией $$ \vec E(t, x)=\vec E_0\cos(\omega t-kx+\varphi).\quad\quad (1) $$ Здесь $\vec E, \vec E_0$ – напряженность электрического поля волны и его амплитуда соответственно, величина $k$ называется волновым числом, $\omega$ – круговая частота волны, $\varphi$ – начальная фаза, а величина под косинусом носит название фазы волны.

1 ^0.80 Выразите волновое число $k$ через длину волны $\lambda$, а период колебаний $T$ через угловую частоту $\omega$.

2 ^0.40 Выразите скорость распространения волны $c$ через величины $k$ и $\omega$.

В общем случае плоская монохроматическая волна описывается функцией $$\vec E(t, \vec r)=\vec E_0\cos(\omega t-\vec k\cdot \vec r+\varphi).\quad\quad (2)$$ В данном выражении $r$ – радиус-вектор произвольной точки пространства, $k$ – волновой вектор, равный по модулю волновому числу и указывающий направление распространения волны. Пусть волновой вектор $\vec k$ лежит в плоскости $Oxy$ и направлен под углом $\theta$ к оси $Ox$, как показано на рисунке справа.

3 ^0.20 Нарисуйте схематически семейство эквидистантных волновых поверхностей, то есть поверхностей равной фазы колебаний, для плоской волны, описываемой функцией (2).

4 ^0.20 Запишите явное выражение для напряженности электрического поля волны (2), как функцию координат $\vec E(t, x, y)$.

Идеальная монохроматическая волна бесконечна во времени и пространстве, поэтому она не может нести информацию. Для передачи информации необходимо использовать либо отдельные импульсы (ограничивать волну во времени) или изменять амплитуду волны (модулировать волну). В этих случаях волна перестает быть монохроматической, и ее можно представить в виде суммы (суперпозиции) монохроматических волн. Рассмотрим волну, являющуюся суммой двух волн, распространяющихся вдоль оси $Ox$: первая с круговой частотой $\omega_0$ и волновым числом $k_0$; частота второй волны равна $\omega_0+\Delta\omega$, $\Delta\omega\ll\omega_0$, а ее волновое число – $k_0+\Delta k$, $\Delta k\ll k_0$. Заметим, что в общем случае волновое число является некоторой функцией от частоты $k(\omega)$.

5 ^0.40 Покажите, что сумма двух этих монохроматических волн представляет собой модулированную волну, состоящую из отдельных волновых пакетов. Запишите формулу, описывающую медлен-ное изменение амплитуды волны $A_0(x, t)$ в пространстве и времени (ее огибающую).

6 ^0.40 Определите длительность $\tau$ отдельного волнового пакета. Запишите соотношение между длительностью $\tau$ и разностью частот $\Delta\nu=\Delta\omega/2\pi$.

7 ^0.20 Определите пространственную длину волнового пакета $L$.

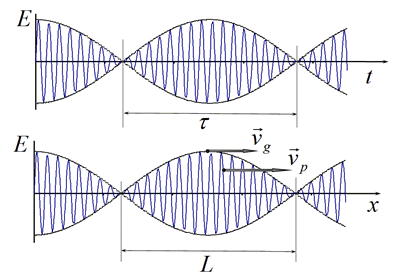
Оказывается, что скорости движения волновой поверхности постоянной фазы $v_p$, которая называется фазовой скоростью, отличается от скорости движения волнового пакета $v_g$, которая называется групповой скоростью. В качестве групповой скорости можно рассматривать скорость движения какого-либо максимума огибающей.

8 ^0.40 Найдите фазовую скорость $v_p$ рассматриваемой модулированной волны и выразите ее через $\omega, k, \Delta\omega, \Delta k$.

9 ^0.40 Найдите групповую скорость $v_g$ рассматриваемой модулированной волны и выразите ее через $\omega, k, \Delta\omega, \Delta k$.

10 ^0.60 Установите связь между фазовой $v_p$ и групповой $v_g$ скоростями для электромагнитных волн в вакууме.

Плоский волновод

В данной части рассмотрим распространение электромагнитных волн в плоском волноводе. Волновод образован двумя бесконечными параллельными проводящими пластинами, находящимися на расстоянии $a$ друг от друга. Считайте, что между пластинами находится вакуум. Будем рассматривать электромагнитные волны, вектор напряженности электрического поля $\vec E$ которых направлен параллельно пластинам (их называют ТЕ-волны). Введем систему координат, ось $Ox$ которой лежит на одной из пластин, а ось $Oy$ направлена перпендикулярно пластинам. Волна, распространяющаяся между пластинами вдоль оси , описывается функцией $$E(t, x, y)=E_0\cos(\omega t-k_x x)\sin(k_y y).\quad\quad (3)$$ где $\omega$– заданная круговая частота волны. Чтобы эта волна могла распространяться в волноводе без потерь энергии, необходимо, чтобы напряженность поля на пластинах обращалась в ноль.

11 ^0.20 Найдите значения $k_y$, при которых волна может распространяться в волноводе без потерь энергии.

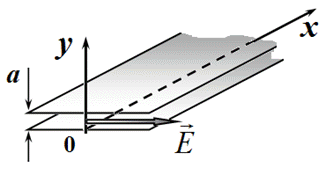
Набор возможных значений $k_y$ является дискретным и характеризуется некоторым целым числом $m$. Волны, соответствующие различным значениям этого числа, называются модами (типами возможных волн).

12 ^1.00 Покажите, что волна, описываемая функцией (3), может быть представлена в виде суперпозиции двух плоских волн $E_1(t,x,y)$ и $E_2(t,x,y)$ с волновыми числами $k_0$, распространяющихся симметрично под углами $\pm\theta$ к пластинам (смотрите рисунок выше).

13 ^0.40 Выразите значения величин $k_x, k_y$ через волновое число волны $k_0$ и угол $\theta$.

14 ^0.60 Определите возможные углы $\theta_m$, при которых волна может распространяться в волноводе без потерь энергии. Выразите значения этих углов через расстояние между пластинами $a$ и длину волны $\lambda$ в вакууме.

15 ^0.60 Определите фазовые скорости $v_p$ волн каждой моды. Выразите эти скорости через частоту волны $\omega$ и скорость света в вакууме $c$.

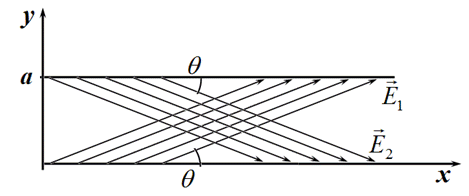
На вход волновода подаются короткие импульсы длительностью $\tau$ с несущей частотой $\omega_0$. Так как эти импульсы имеют конечную длительность, то они не является монохроматической волной, а содержат набор монохроматических компонент в некотором диапазоне частот $\Delta\omega\ll\omega_0$. Эти входные импульсы формируют набор импульсов в каждой из возможных мод волновода.

16 ^1.00 Определите скорость распространения этого импульса в моде номер $m$.

17 ^1.60 На каком минимальном расстоянии $X$ от входа в волновод число импульсов удвоится, если $a/\lambda=1.2$. Ответ выразите через скорость света $c$и длительность импульса $\tau$.

Чтобы избежать появления «лишних» импульсов при передаче информации, используют работающие в одномодовом режиме волноводы, в которых может распространяться только одна мода.

18 ^0.60 Найдите отношения $a/\lambda$, при которых в волноводе может распространяться только одна мода.