Функция
\[
\vec{E}(t, x)=\vec{E}_{0} \cos (\omega t-k x+\varphi)
\]
описывающая волну в фиксированный момент времени \( t=t_{0}, \) дает распределение напряженности поля в пространстве. При изменении координаты на длину волны \( \lambda \) аргумент косинуса должен измениться на \( 2 \pi, \) поэтому
\[
\left(\omega t_{0}-k(x+\lambda)+\varphi\right)-\left(\omega t_{0}-k x+\varphi\right)=2 \pi
\]
Из этого соотношения следует, что
\[
k=\frac{2 \pi}{\lambda}
\]
Фиксируя точку пространства \( x=x_{0} \) и рассуждая аналогично, можно записать
\[
\left(\omega(t+T)-k x_{0}+\varphi\right)-\left(\omega t-k x_{0}+\varphi\right)=2 \pi
\]
откуда следует
\[
\omega=\frac{2 \pi}{T}
\]

Скорость распространения монохроматической волны есть скорость движения некоторой волновой поверхности постоянной фазы. Эта поверхность удовлетворяет уравнению \( \omega t-k x+\varphi= \mathrm{const} \). Из этого уравнения следует, что скорость распространения волны равна
\[
c=\frac{d x}{d t}=\frac{\omega}{k}
\]

Поверхность постоянной фазы в фиксированный момент времени удовлетворяет уравнению \( \vec{k} \cdot \vec{r}= \mathrm{const} \), а это есть семейство плоскостей, перпендикулярных волновому вектору \( \vec{k} \).

Ответ:

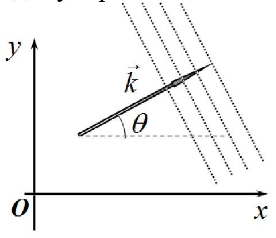
Раскрывая скалярное произведение $\vec{k} \cdot \vec{r} $ получим уравнение волны в координатном представлении:

Так как для напряженности электрического поля справедлив принцип суперпозиции, то для составной волны можно записать
\[
\begin{array}{l}
E=E_{0} \cos \left(\omega_{0} t-k_{0} x\right)+E_{0} \cos \left(\left(\omega_{0}+\Delta \omega\right) t-\left(k_{0}+\Delta k\right) x\right)= \\
=2 E_{0} \cos \left(\left(\omega_{0}+\frac{\Delta \omega}{2}\right) t-\left(k_{0}+\frac{\Delta k}{2}\right) x\right) \cos \left(\frac{\Delta \omega}{2} t-\frac{\Delta k}{2} x\right)
\end{array}
\]
Учтем, что \( \Delta \omega\ll\omega_{0}, \) а, следовательно, и \( \Delta k\ll k_{0}, \) перепишем это выражение в виде: \( E=A_{0}(x, t) \cos \left(\omega_{0} t-k_{0} x\right) \)
Здесь введено обозначение
\[
A_{0}(x, t)=2 E_{0} \cos \left(\frac{\Delta \omega}{2} t-\frac{\Delta k}{2} x\right)
\]
для медленно изменяющейся амплитуды волны.

Для определения длительности пакета следует учесть, что при переходе от одного «нуля» косинуса до следующего аргумент косинуса изменяется на \( \pi \). Поэтому \( \cfrac{\Delta \omega}{2} \tau=\pi \Rightarrow \tau=\cfrac{2 \pi}{\Delta \omega} \).
Учитывая, что \( \Delta \omega=2 \pi \Delta v, \) получим соотношение между длительностью пакета и его спектральной шириной:

Проводя аналогичные рассуждения, не сложно получить, что
\[
\frac{\Delta k}{2} L=\pi \Rightarrow L=\frac{2 \pi}{\Delta k}
\]

Фазовая скорость может быть найдена как скорость движения волновой поверхности постоянной фазы. Из п. 5 следует, что эта поверхность удовлетворяет условию \( \left(\omega_{0} t-k_{0} x\right)= \) const
из которого следует, что фазовая скорость равна

Для определения групповой скорости, запишем условие того, что амплитуда волны, например, максимальна
\[
\frac{\Delta \omega}{2} t-\frac{\Delta k}{2} x=0
\]
Из этого выражения следует, что групповая скорость задается формулой

Для электромагнитных волн в вакууме выполняется соотношение \( \lambda\nu=c, \) из которого следует
\[
\omega=k c
\]
откуда находим
$$
v_{p}=\cfrac{\omega}{k}=c \\
v_{g}=\cfrac{\Delta \omega}{\Delta k}=c=v_{p}
$$
то есть, и фазовая, и групповая скорости равны скорости света \( c \) в вакууме.

Предложенная в условии функция, описывающая поле в плоском волноводе
\[
E(t, x, y)=E_{0} \cos \left(\omega t-k_{x} x\right) \sin \left(k_{y} y\right)
\]
удовлетворяет одному граничному условию: при \( y=0 \quad \) напряженность поля \( E=0 . \) Поэтому следует выбрать такие значения \( k_{y}, \) чтобы выполнялось второе граничное условие: при \( y=a \) напряженность поля также должна обращаться в нуль. Это условие будет выполнено при
\[
\sin k_{y} a=0 \Rightarrow k_{y} a=m \pi \Rightarrow k_{y}=m \frac{\pi}{a}
\]
В этом выражении \( m- \) целое положительное число, \( m=1,2,3 \ldots \)

Запишем уравнения симметричных волн
\[
\begin{array}{l}
E_{1}=E_{0}^{\prime} \cos \left(\omega t-k_{0} x \cos \theta+k_{0} y \sin \theta+\varphi\right) \\
E_{2}=E_{0}^{\prime} \cos \left(\omega t-k_{0} x \cos \theta-k_{0} y \sin \theta-\varphi\right)
\end{array}
\]
где \( k_{0}=\cfrac{\omega}{c}- \) волновое число волн, распространяющихся под углом \( \pm \theta \) к плоскостям волновода, и просуммируем их
\[
E=E_{1}+E_{2}=2 E_{0}^{\prime} \cos \left(\omega t-k_{0} x \cos \theta\right) \cos \left(k_{0} y \sin \theta+\varphi\right)
\]
то есть должно выполняться условие
\[
E_{0}^{\prime}=E_{0} / 2
\]
Отметим при этом, что должно быть \( \varphi=-\pi / 2 . \)

Из сравнения полученной формулы и формулы для плоского волновода в п. 11 следует, что они будут совпадать, если

Приравнивая значения величины \( k_{y} \), выражаемые формулами в п. 11 и 13, находим
\[
k_{y}=k_{0} \sin \theta_{m}=m \frac{\pi}{a} \Rightarrow \sin \theta_{m}=m \frac{\pi}{a k_{0}}
\]
Волновое число рассматриваемых волн в вакууме связано с длиной волны соотношением
\[
k_{0}=\frac{2 \pi}{\lambda}
\]
тогда значения возможных углов задаются формулой
\[
\sin \theta_{m}=m \frac{\pi}{a k_{0}}=m \frac{\lambda}{2 a}
\]

Из уравнений п. 11 следует, что фазовая скорость распространения волны в волноводе задается формулой
\[
v_{p}=\frac{\omega}{k_{x}}=\frac{\omega}{k_{0} \cos \theta}
\]
Выразив значение косинуса угла через его синус, который определяется формулой в п. 14, находим \[
v_{p}=\frac{\omega}{k_{0} \cos \theta}=\frac{\omega}{k_{0} \sqrt{1-\sin ^{2} \theta}}=\frac{\omega}{k_{0} \sqrt{1-\left(m \frac{\lambda}{2 a}\right)^{2}}}
\]
Наконец, используя формулы, связывающие частоты, длины волн и скорость света в вакууме \( \cfrac{\omega}{k_{0}}=c, \lambda=\cfrac{2 \pi}{\omega} c, \) получим
\[
v_{p}=\cfrac{\omega}{k_{0} \cos \theta}=\cfrac{\omega}{k_{0} \sqrt{1-\sin ^{2} \theta}}=\cfrac{c}{\sqrt{1-\left(m \cfrac{\pi c}{\omega a}\right)^{2}}}
\]
Таким образом, оказывается, что фазовая скорость распространения незатухающей волны в волноводе больше, чем скорость света в вакууме.

Скорость распространения импульса есть групповая скорость распространения, поэтому она определяется формулой п. 9, в которой отношение приращений можно заменить производной
\[
v_{g}=\frac{\Delta \omega}{\Delta k}=\frac{d \omega}{d k}=\left(\frac{d k}{d \omega}\right)^{-1}
\]
Для вычисления скорости по этой формуле необходимо получить в явном виде зависимость волнового числа от частоты \( k(\omega) . \) Для этого воспользуемся общей формулой для фазовой скорости
\( v_{p}=\cfrac{\omega}{k} \) и запишем
\[
k=\frac{\omega}{v_{p}}=\frac{\omega}{c} \sqrt{1-\left(m \frac{\pi c}{\omega a}\right)^{2}}=\frac{1}{c} \sqrt{\omega^{2}-\left(m \frac{\pi c}{a}\right)^{2}}
\]
после чего скорость распространения импульса вычисляется как
\[
v=v_{g}=\left(\cfrac{d k}{d \omega}\right)^{-1}=\left(\cfrac{1}{c} \frac{\omega}{\sqrt{\omega^{2}-\left(m \cfrac{\pi c}{a}\right)^{2}}}\right)^{-1}=c \sqrt{1-\left(m \cfrac{\pi c}{a \omega}\right)^{2}}
\]
Как следует из этой формулы, групповая скорость, естественно, меньше скорости света в вакууме. Также, следует указать, что эта скорость равна \( c \cos \theta, \) что вполне очевидно.

Обратимся к формуле п. 14 и подставим в нее заданное отношение \( a \) / \( \lambda=1.2 \)
\[
\sin \theta_{m}=m \frac{\lambda}{2 a} \approx 0,42~\text{м}
\]
Так как синус любого аргумента не превышает единицы, то из полученного выражения следует, что в данном волноводе могут распространяться только две моды с \( m=1 \) и \( m=2, \) иными словами, входной импульс будет возбуждать в волноводе два импульса в этих модах. Скорости распространения импульсов в различных модах будут заметно различаться. Прежде всего, выразим эти скорости через заданное отношение \( a / \lambda \) в виде
\[
v=c \sqrt{1-\left(m \frac{\pi c}{a \omega}\right)^{2}}=c \sqrt{1-\left(m \frac{\lambda}{2 a}\right)^{2}}
\]
На входе в волновод импульсы в обеих модах возбуждаются одновременно, но так как они движутся с разными скоростями, то по мере возрастания пройденного расстояния они расходятся во времени. Число импульсов удвоится, когда импульсы в разных модах разойдутся на время, превышающее длительность импульса, поэтому искомое расстояние \( X \) можно найти из условия
\[
\frac{X}{v_{2}}-\frac{X}{v_{1}}=\tau
\]
которое приводит к окончательному ответу \( X=\cfrac{\tau}{\cfrac{1}{v_{2}}-\cfrac{1}{v_{1}}}=\cfrac{c \tau}{\sqrt{1-\left(\cfrac{\lambda}{2 a}\right)^{2}}-\cfrac{1}{\sqrt{1-\left(2 \cfrac{\lambda}{2 a}\right)^{2}}}} \approx 1.4\;c \tau \)

Для того, чтобы волновод был одномодовым необходимо, чтобы выполнялось условие $\sin \theta_{2}=2 \cfrac{\lambda}{2 a}>1$ или $ \cfrac{a}{\lambda}<1$.